 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Несобственные интегралы. Определённый интеграл называют собственным интегралом ⇐ ПредыдущаяСтр 7 из 7
Определённый интеграл Несобственный интеграл I рода (интеграл с бесконечным промежутком интегрирования) Пусть подынтегральная функция f(x) непрерывна и ограничена для всех
Если этот предел существует и он конечен, то несобственный интеграл Аналогичным образом определяется несобственный интеграл на промежутке
Несобственный интеграл с двумя бесконечными пределами определяется формулой
где с – произвольное число. В данном случае интеграл слева сходится в том случае, когда сходятся оба интеграла справа. Примеры.Вычислить несобственные интегралы или установить их расходимость: 1. 2. = 3. 4. Определить площадь фигуры, ограниченной кривой =
Рис. 7.19. Признаки сравнения Приведём без доказательства один из признаков сходимости несобственных интегралов I рода. Теорема. Если на промежутке Пример.Исследовать сходимость интеграла
Несобственный интеграл II рода (интеграл от разрывной функции) Пусть функция f(x) непрерывна на промежутке
Если предел в правой части существует, то несобственный интеграл Если функция f(x) имеет разрыв в точке с на промежутке [a, b], то несобственный интегралом II рода определяется формулой
В этом случае интеграл слева сходится, если оба несобственных интегралов справа являются сходящимися. Примеры.Вычислить или установить сходимость несобственного интеграла: 1.
2.
интеграл расходится.
Поиск по сайту: |
 называют собственным интегралом, если промежуток интегрирования
называют собственным интегралом, если промежуток интегрирования  конечен, а подынтегральная функция f(x) непрерывна на этом отрезке. В данном разделе рассматриваются так называемые несобственные интегралы, т.е. определённый интеграл от непрерывной функции, но с бесконечным промежутком интегрирования, либо определённый интеграл с конечным промежутком интегрирования, но от функции, имеющей в этом интервале бесконечный разрыв.
конечен, а подынтегральная функция f(x) непрерывна на этом отрезке. В данном разделе рассматриваются так называемые несобственные интегралы, т.е. определённый интеграл от непрерывной функции, но с бесконечным промежутком интегрирования, либо определённый интеграл с конечным промежутком интегрирования, но от функции, имеющей в этом интервале бесконечный разрыв. . Несобственный интегралом первого рода обозначается символически как
. Несобственный интегралом первого рода обозначается символически как 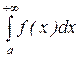 . Несобственным интегралом от функции f(x) на бесконечном промежутке
. Несобственным интегралом от функции f(x) на бесконечном промежутке  называется предел, если он существует, при
называется предел, если он существует, при 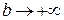 определённого интеграла
определённого интеграла  , т.е.
, т.е.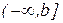
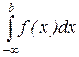 =
=  . (7.22)
. (7.22) =
= 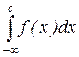 +
+ 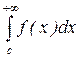 , (7.23)
, (7.23)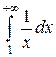 =
= 
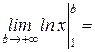
 , интеграл расходится;
, интеграл расходится;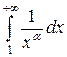 =
= 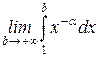 =
= 
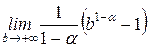 =
= ;
; =
= 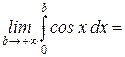

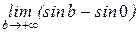 , интеграл расходится, так как при
, интеграл расходится, так как при 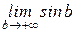 не существует.
не существует.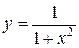 и осью Ох
и осью Ох  =
=  =
= 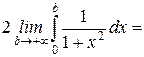

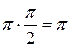 .
.
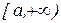 для непрерывных функций удовлетворяется неравенство 0
для непрерывных функций удовлетворяется неравенство 0  , то из сходимости интеграла
, то из сходимости интеграла 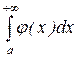 следует сходимость интеграла
следует сходимость интеграла 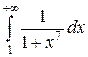 . Подынтегральная функция
. Подынтегральная функция 
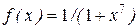 в промежутке интегрирования меньше чем
в промежутке интегрирования меньше чем 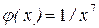 , а интеграл
, а интеграл 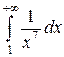 является сходящимся. Следовательно, данный интеграл также сходится.
является сходящимся. Следовательно, данный интеграл также сходится.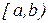 и имеет бесконечный разрыв в точке х = b . Несобственным интегралом II рода
и имеет бесконечный разрыв в точке х = b . Несобственным интегралом II рода  называется конечный предел, если он существует, интеграла
называется конечный предел, если он существует, интеграла 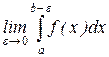 . Таким образом, по определению,
. Таким образом, по определению,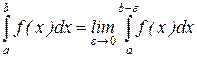 . (7.18)
. (7.18) .
. . При х = 1 функция
. При х = 1 функция  терпит бесконечный разрыв.
терпит бесконечный разрыв.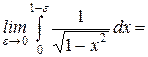

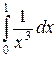 . При х = 0 функция
. При х = 0 функция  терпит бесконечный разрыв.
терпит бесконечный разрыв.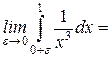
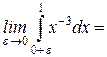

 ,
,