 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение длины дуги плоской кривой
Прямоугольные координаты Пусть в прямоугольных координатах задана плоская кривая АВ, уравнение которой
Рис. 7.16. Длина ломаной линии, которая соответствует дуге M0Mn , может быть найдена как сумма Из геометрических соображений: Тогда
Пример. Вычислить длину дуги кубической параболы Так как
= Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции, из формулы (7.9) получаем
= где х = x(t), a = x(α) и у = у(t), b=y(β). Таким образом, если уравнение кривой задано в параметрической форме, то длина кривой находится по формуле
Пример. Найти длину первой арки циклоиды
Находим производные
= = Если задана пространственная кривая, и х = x(t), у = y(t) и z = z(t), то
Полярные координаты Пусть кривая задана в полярных координатах
и длину кривой находим по формуле (7.10), выполнив соответствующие преобразования
Поэтому = В результате длина кривой определяется формулой
Пример. Найти длину кардиоиды
Рис. 7.17 может быть получена как траектория точки окружности С1, катящейся без скольжения по окружности С того же радиуса а. Когда φ пробегает промежуток (-π, +π), кардиоида описывается полностью. Длина её согласно (7.12) равна
Таким образом, длина кардиоиды равна восьмикратному диаметру производящего круга. Вычисление объёма тела Вычисление объема тела по известным площадям его поперечных Сечений Пусть имеется тело объема V. Площадь любого поперечного сечения тела S, известна как непрерывная функция S = S(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция S(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.
Рис. 7.18 Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны MiDxi и miDxi здесь Dxi = xi+1 - xi. Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:
Таким образом, объем тела может быть найден по формуле:
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию S(x), что весьма проблематично для тел сложной формы. Объём тела вращения Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения (рис. 7.19).
Рис. 7.19. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох ( Применяя формулу (7.13) объёма тела по площади поперечных сечений, получаем
Пример.Определить объём тела, образованного вращением фигуры, ограниченной линиями y = x2 , x = 1, x = 2 (рис. 7.20).
Рис. 7.20. Решение. По формуле (7.14) находим
7.4.4. Механические приложения определённого интеграла\
Поиск по сайту: |
 , где
, где  . Если
. Если  и
и  непрерывны, то такие кривые называются гладкими. Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число сторон ломаной неограниченно возрастает, а длина набольшей из сторон ломаной стремится к нулю.
непрерывны, то такие кривые называются гладкими. Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число сторон ломаной неограниченно возрастает, а длина набольшей из сторон ломаной стремится к нулю.
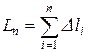 , где
, где  - длина стороны ломаной на участке
- длина стороны ломаной на участке  (рис. 7.16). Тогда длина дуги M0Mn равна
(рис. 7.16). Тогда длина дуги M0Mn равна  .
. , но в то же время
, но в то же время 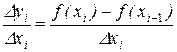 .
.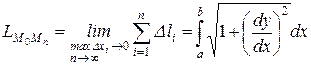 . Т.е. длина дуги M0Mn при изменении х от а до b равна
. Т.е. длина дуги M0Mn при изменении х от а до b равна . (7.9)
. (7.9) , находящейся между точками
, находящейся между точками  и
и  .
. , то
, то  . Поэтому искомая длина дуги согласно формуле (7.9) определяется следующим образом
. Поэтому искомая длина дуги согласно формуле (7.9) определяется следующим образом
 .
. =
=
 ,
, . (7.10)
. (7.10)

 и
и  . По формуле (7.10) длина арки циклоиды
. По формуле (7.10) длина арки циклоиды =
=
 .
. . (7.11)
. (7.11) ,
,  , причем функция
, причем функция 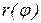 и
и  непрерывны на отрезке [α, β]. Воспользуемся формулами связи между полярными и декартовыми координатами
непрерывны на отрезке [α, β]. Воспользуемся формулами связи между полярными и декартовыми координатами  ,
,  , тогда считая угол φ параметром, можно задать уравнение кривой в параметрической форме
, тогда считая угол φ параметром, можно задать уравнение кривой в параметрической форме

 =
= .
. . (7.12)
. (7.12) . Кардиоида, изображённая на рисунке
. Кардиоида, изображённая на рисунке



 и
и  .
. .
. . (7.13)
. (7.13)
 ), есть круг с радиусом y = f(x). Следовательно, площадь поперечного сечения S(x) = π y2.
), есть круг с радиусом y = f(x). Следовательно, площадь поперечного сечения S(x) = π y2.  . (7.14)
. (7.14)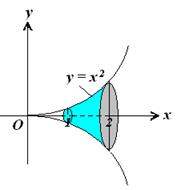
 =
=  .
.