 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Центр тяжести плоской фигуры
Согласно закону всемирного тяготения все тела притягиваются к Земле с силой, пропорциональной массе тела ( При рассмотрении равновесия и движения тел сложной формы важно знать положение центра тяжести этого тела. Рассмотрим определение положения центра тяжести материальной пластины АВВ1А1 в виде криволинейной трапеции, ограниченной сверху кривой АВ, которая задана явным уравнением у = у(х), и линиями х = а, х = b ( a < b) и у = 0 (Рис. 7.21).
Рис. 7.21 Предположим, что поверхностная плотность материала пластины постоянна, т.е. фигура однородна. Можно для определенности считать, что удельный вес материала пластины равен 1 ( γ = ρ g = 1, ρ – плотность материала), тогда масса пластины или её любой части измеряется соответствующей площадью. Для определения положения центра тяжести проведём разбиение рассматриваемой пластины на вертикальные полосы с основаниями
где Центром тяжести рассматриваемой однородной пластины АВВ1А1 , также как любого другого тела, обладает тем свойством, что его положение не зависит от поворота данной пластины на любой угол по отношению к вертикали. Как показано в курсе теоретической механики координаты центра тяжести тела определяется формулами
когда количество разбиений стремится к бесконечности, а длина элементов разбиения
Переходя к пределу в формулах (7.15), когда
где y = y(x) – уравнение кривой АВ. Замечания. 1. Если плоская фигура имеет ось или центр симметрии, то центр тяжести такой фигуры находится на оси или в центре симметрии. 2. Если тело состоит из частей, центры тяжести которых известны, то центр тяжести составной фигуры определяется по формулам
здесь k – количество составных частей; Si и хi, уi – соответственно площадь и координаты центра тяжести i-ой части. Если же плоская фигура имеет отверстия, то центр тяжести этой фигуры определяется по этим же формулам, однако площади, соответствующие отверстиям должны быть отрицательными. Пример. Определить координаты центра тяжести четверти круга
Площадь четверти круга Определяем интегралы числителей формул (7.16) (эти интегралы называются статическими моментами)
Таким образом, координаты центра тяжести четверти круга равны
Поиск по сайту: |
 m - масса тела и g = 9,81 м/с2 ), эта сила называется весом тела (силой тяжести).
m - масса тела и g = 9,81 м/с2 ), эта сила называется весом тела (силой тяжести).
 i = 1,2,…,n (
i = 1,2,…,n (  ). Центр тяжести каждой полосы определяется координатами
). Центр тяжести каждой полосы определяется координатами ,
,  ,
, и
и 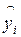 - координаты точки кривой
- координаты точки кривой 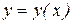 (
(  ,
,  , (7.15)
, (7.15) . В формулах (7.15)
. В формулах (7.15)  - площадь i – ой полосы разбиения
- площадь i – ой полосы разбиения (
(  и
и  ,
,  , (7.16)
, (7.16) ,
,  ,
, (х, у > 0) . Изобразим данную плоскую фигуру
(х, у > 0) . Изобразим данную плоскую фигуру
 .
.
 ,
, .
. ,
,  .
.