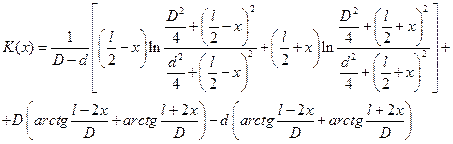|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические положения. Федеральное агентство по образованию Российской Федерации
Федеральное агентство по образованию Российской Федерации Филиал «Севмашвтуз» государственного образовательного учреждения высшего профессионального образования «Санкт – Петербургский государственный морской технический университет» В г. Северодвинске
Факультет: № 4 Кафедра: № 12
Лабораторная работа
ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА С ПОМОЩЬЮ ДАТЧИКА ХОЛЛА
Г. Северодвинск ЛАБОРАТОРНАЯ РАБОТА ФПЭ - 04 ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА С ПОМОЩЬЮ ДАТЧИКА ХОЛЛА Цель работы Ознакомление с методом измерения индукции магнитного поля, экспериментальное исследование пространственного распределения индукции вдоль оси соленоида.
Основные теоретические положения Опыт показывает, что между двумя движущимися электрическими зарядами или токами в проводниках, действуют особые силы, отличные от сил, действующих между неподвижными зарядами. Вид материи посредством которой осуществляется это взаимодействие, называется магнитным полем. Основной характеристикой магнитною поля является магнитная индукция В. Магнитная индукция векторная величина, численно равная силе, действующей со стороны магнитного поля на единицу длины проводника, с током равным единице, расположенного перпендикулярно вектору В. Часто на практике необходимо знать распределение магнитного поля проводников с током произвольной формы. Особый интерес представляет соленоид – проводник, свернутый в виде прямой цилиндрической спирали, витки которой располагаются вплотную друг к другу. Вычислить индукцию магнитного поля соленоида можно с помощью закона Био-Савара-Лапласа
и принципа суперпозиции.
где μ – магнитная проницаемость среды, для воздуха принять μ, μ0 – магнитная постоянная, рапная
Рис.1 После математических вычислениймодуль магнитной индукции в произвольной точке на оси многослойного соленоида конечных размеров будет
где N – число витков, l – длина соленоида, I – ток, протекающий по нему, D, d – внешний и внутренний диаметры соленоида, х – координата точки на оси относительно т. О, Здесь за K(x) мы обозначили:
Рис.2 Формула (3) описывает чётную функцию координаты х, поэтому её график будет симметричен относительно точки О, а максимум достигается в середине соленоида. В работе предлагается сравнить рассчитанную по формуле (3) и экспериментально измеренную зависимость магнитной индукции от координаты x вдоль соленоида.
Поиск по сайту: |
 (1)
(1) (2)
(2)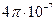 Гн/м,
Гн/м,  - элемент проводника с током I,
- элемент проводника с током I,  - расстояние от элемента проводника до точки А, где вычисляетсяиндукция (рис.1).
- расстояние от элемента проводника до точки А, где вычисляетсяиндукция (рис.1).
 (3)
(3)