 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Аналитическое определение геометрических и кинематических параметров механизма.
Санкт-Петербургский институт машиностроения Кафедра теории и конструирования Механических систем машиностроения
Структурный и кинематический расчет механизма Расчётно-графическая работа по ТММ Выполнил ст. Группа
Исходные данные Механизм- кривошипно –ползунный (центральная схема); наибольший ход ползуна м отношение длины кривошипа к длине шатуна λ=ОА/АВ = ;
частота вращения ротора двигателя, об/мин – n1=
угол поворота кривошипа, определяющий положение механизма, в котором производятся построения и расчёты
Определение размеров механизма радиус кривошипа ОА=0,5
длина шатуна АВ=ОА/λ= =м
По полученным размерам вычерчивается в масштабе схема механизма в положении
Структурный анализ механизма:. За наиболее часто применяемыми звеньями закреплены специальные названия: 1-кривошип, совершает вращательное движение; 2-шатун, совершает сложно-плоское движение, не имеет неподвижных точек: 3-ползун, совершает возвратно-поступательное движение в неподвижных направляющих стойки 4. Определяем по формуле Чебышева число степеней свободы механизма :w=3(n-1)-2p1-p2. Здесь: n -число звеньев, включая неподвижное: р1-число одноподвижных (вращательных и поступательных кинематических пар), каждая из которых отнимает у механизма две степени свободы. В данном механизме три вращательных пары (1-4), (1-2), (2-3) и одна поступательная (3-4). Сл-но р1=4. Р2 -число двухподвижных пар , каждая из которых отнимает у механизма одну степень свободы. В данном механизме р2=0. Подставляя, получаем w=1. Механизм имеет одну степень свободы. Положение всех звеньев определяется одной независимой координатой (угол поворота кривошипа).
Аналитическое определение геометрических и кинематических параметров механизма. При значениях
= м.
= м.
= м.
Угол поворота шатуна
= рад.
В градусах
Аналог угловой скорости шатуна
= =
Аналог углового ускорения шатуна
= =
Угловая скорость кривошипа (постоянна) = 1/с
Линейная скорость ползуна VB=S′• = . м/с
Ускорение ползуна ав=s"• = м/с2
Угловая скорость шатуна ω2=α′•ω1 = = 1/с
Угловое ускорение шатуна ε2=α″• = 1/с2
Результаты расчётов со знаком “-“ означают направление против оси Х или поворот по часовой стрелке.
Определение скоростей и ускорений методом планов.
Данный метод позволяет определять скорости и ускорения без использования аналитических зависимостей.
Построение плана скоростей Определяем окружную скорость точки А. Вектор
По теореме сложения скоростей в плоском движении для шатуна используется векторное уравнение Здесь VA- скорость переносного поступательного движения вместе с полюсом. VBA- скорость точки В относительно точки А. Так как относительное движение вращательное, линия действия VBA перпендикулярна линии АВ шатуна. Линия скорости VB ползуна совпадает с осью Х. Решаем векторное уравнение построением плана скоростей.
Порядок построения. Из полюса р откладываем VA в виде отрезка ра=100мм перпендикулярно ОА в сторону Масштаб плана скоростей KV=VA/pa = = (м/с)/мм Определяем величины
Построение плана ускорений. Определяем ускорение точки А. Так как угловая скорость кривошипа постоянна, его угловое ускорение =0. Сл-но По теореме сложения ускорений в плоском движении для шатуна используем векторное уравнение Здесь
Кориолисово ускорение в данном случае =0 ( переносное движение поступательное). Так как относительное движение вращательное
Порядок построения. Из полюса q откладываем Из точки Угловое ускорение шатуна ε2= ПЛАН СКОРОСТЕЙ ПЛАН УСКОРЕНИЙ Схема механизма М 1:
Поиск по сайту: |
 =
= =
=
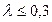 для определения перемещения, аналогов скорости и ускорения ползуна можно использовать приближённые зависимости:
для определения перемещения, аналогов скорости и ускорения ползуна можно использовать приближённые зависимости: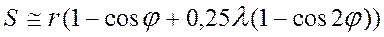 =
= =
= =
= =
= ◦=
◦= =
= =
= =
=  n1/30=
n1/30= направлен перпендикулярно ОА в сторону
направлен перпендикулярно ОА в сторону  .
. = = м/с.
= = м/с. = = м/с. Угловая скорость шатуна ω2=(VBA/AB)= = 1/с . Сравниваем полученные результаты с аналитическими.
= = м/с. Угловая скорость шатуна ω2=(VBA/AB)= = 1/с . Сравниваем полученные результаты с аналитическими.  = = м/с2. Вектор
= = м/с2. Вектор  направлен параллельно ОА к центру вращения.
направлен параллельно ОА к центру вращения. =
=  +
+ 

 +
+  . Центростремительное ускорение
. Центростремительное ускорение  направлено параллельно шатуну от точки В к точке А.
направлено параллельно шатуну от точки В к точке А. перпендикулярна шатуну АВ.
перпендикулярна шатуну АВ. откладываем
откладываем  в виде отрезка
в виде отрезка  параллельно АВ в направлении от точки В к точке А.
параллельно АВ в направлении от точки В к точке А.  = = мм.
= = мм. проводим линию действия
проводим линию действия  перпендикулярно шатуну АВ, а из полюса
перпендикулярно шатуну АВ, а из полюса  линию действия
линию действия  параллельно линии хода ползуна (ось Х). Точка
параллельно линии хода ползуна (ось Х). Точка  пересечения этих линий определяет величины ускорений.
пересечения этих линий определяет величины ускорений.  = = м/с2.
= = м/с2.  = = м/с2.
= = м/с2.