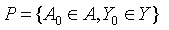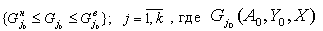|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи структурного и параметрического синтеза
Общая постановка задачи структурного и параметрического синтеза. Результирующее проектное решение (при конструкторском проектировании) ищется на множестве структур А, которые способен создать проектировщик, а также на множестве варьируемых параметров Y. Здесь А и Y образуют множество альтернатив, на которых ищутся решения. Тогда общая форма задачи синтеза ставится так:
Поиск при заданных ограничениях
для достижения экстремума функции. Таким образом, техническое решение представляет собой некоторую структуру и, найденную на множестве структур и параметров, отвечающих ограничениям в среде функционирования Х. Процедуры структурного и параметрического синтеза. Процедуры синтеза выполняются на основе математической модели, являющийся математическим аналогом проектируемого объекта. Степень адекватности (соответствия) модели реальному (будущему) объекту определяется начальной постановкой. Процедуры синтеза и анализа итерационны и образуют два вложенных цикла: – внешний – структурный цикл; – внутренний – параметрический цикл. Vп, Vс – вариация пар (структур). Процедура выбора заключается в выборе некоторых данных для отобранной структуры, на основе чего и строится математическая модель. Основными показателями при реализации цикла является показатель модели, т.е. время реализации одного модельного эксперимента по расчету критериальных показателей при заданном векторе варьируемых параметров. Это модельное время. Используются различные методы для варьирования значений параметров, в том числе: а) полный перебор (сканирование), при котором задается верхние и нижние значения параметров и задается ∆yi б) метод случайного поиска. Внешний цикл – это перебор структур, часто он делается вручную. Точка 1 – выход – найдено проектное решение. Точка 2 – при неблагоприятном исходе, т.е. невозможности найти решение на обозримом числе структур в пределах заданного пространства поиска система выводит на точку 2 процедуру принятия решения. Здесьсуществует 2 альтернативы принятия решения: 1 альтернатива проектировщика: перенос ряда независимых параметров Х (внешних ограничений) в число варьируемых параметров Y; 2 альтернатива заказчика: уступки заказчика – снижение требований на ряд некоторых качественных характеристик Если альтернатива 1 – это уступка нам со стороны смежных проектировщиков, то 2 – это уступка заказчика. Задачи оптимизации Задача повышения эффективности технологических и организационных систем (например: металлорежущего станка, автоматической линии, производства в целом) путём принятия обоснованных решений актуальна во всех областях деятельности человека. Количественная оценка эффективности может быть получена при заданной цели функционирования системы, с учётом ограничений на ресурсы, привлекаемые для достижения цели. При этом задача принятия решения ставится как задача выбора параметров системы, обеспечивающих максимизацию или минимизацию целевой функции. Последняя количественно определяет степень достижения цели – величину критерия оптимизации. В качестве критерия можно принять, например, себестоимость изделия (цель-минимизация), быстродействие машины или прибора (цель-максимизация) и другие показатели. В процессе оптимизации, с учетом заданных условий, отыскиваются элементы решения, т.е. те параметры системы и показатели качества, которые зависят от выбора и приводят к отыскиванию оптимальных конструкций, технологических схем и др. Всякая оптимизационная задача предполагает заданной целевую функцию – количественный показатель качества альтернатив выбора. Обычно в задачах оптимизации отыскивается экстремум интегрального показателя, который представляется одной функцией f(X) нескольких переменных, заданной в некоторой области допустимых значений переменных. Наименьшее или наибольшее значения целевой функции из всех возможных в заданной области R называютсяглобальными экстремумами . Значение X, при котором достигается глобальный экстремум, называется точкой глобального экстремума. Локальный экстремум функции f(X) – значение f (Х°) этой функции такое, что для любогоХ из R, близкого к Х° из R, справедливо f (Х°) ≥ f (X) (локальный максимум) или f (Х°) ≤ f (X) (локальный минимум). Обоснованное применение количественных методов для принятия решений – оптимизацию поведения структур систем называют исследованием операций (ИСО). Здесь операция – комплекс целенаправленных действий. Задача, рассмотренная выше, решается с применением математической модели системы, объединяющей упомянутые ограничения на ресурсы и целевую функцию. Нахождение величин упомянутых параметров системы (они входят в математическую модель как неизвестные) путём решения математической задачи называютматематическим программированием . Математическое программирование – важнейшая область математики, ориентированная на широкое применение компьютеров. В зависимости от характера целевой функции, а также ограничений могут использоваться различные методы оптимизации (математического программирования): линейное программирование, нелинейное программирование (хотя бы одна из функций нелинейна по X), целочисленное линейное программирование, динамическое программированиеи др.
Поиск по сайту: |