 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
АНАЛИЗ ЦЕПЕЙ ПОСТОЯННОГО ТОКА С НЕЛИНЕЙНЫМИ РЕЗИСТИВНЫМИ ЭЛЕМЕНТАМИ
Нелинейными электрическими элементами являются элементы, параметры которых зависят от тока и напряжения. Цепи, содержащие такие элементы, именуемые электрическими нелинейными цепями, обладают рядом новых свойств, которые отсутствуют у линейных цепей. Эти свойства позволяют создать основанные на них автоматические системы управления и регулирования, устройства для преобразования электромагнитной энергии, устройства для производства электрических измерений и передачи информации, быстродействующие вычислительные машины и т.д. Особенностью и сложностью анализа нелинейных систем является невозможность применения принципа наложения. К нелинейным электрическим цепям постоянного тока относятся электрические цепи, содержащие нелинейные сопротивления, обладающие нелинейными вольт-амперными характеристиками, т.е. зависимость напряжения на зажимах резистивного нелинейного элемента от тока в нем задается его вольтамперной характеристикой (ВАХ). Вольт-амперные характеристики могут быть заданы в виде графиков, таблиц и аналитических выражений. Статическими называют характеристики, в которых каждая точка дает значение постоянного напряжения при соответствующем значении постоянного тока. Из них определяют статическое сопротивление и статическую проводимость нелинейного элемента
Электрическое состояние нелинейных цепей постоянного тока описывается системой алгебраических уравнений, составленных по первому и второму закону Кирхгофа. Общих аналитических методов решения нелинейных уравнений не существует, поэтому решение таких задач осуществляется численными методами с использованием ЭВМ. Однако существуют наиболее простые методы расчета цепей постоянного тока с резистивными элементами - графические и графоаналитические: метод эквивалентных преобразований и метод пересечения характеристик. Метод эквивалентных преобразований для нелинейных цепей, так же как и для линейных, основан на замене нескольких элементов одним и сводится к нахождению ВАХ эквивалентного нелинейного элемента. При расчете электрических цепей с последовательным или параллельным включением нелинейных (или линейных и нелинейных) сопротивлений их вольт-амперные характеристики представляются в общей координатной системе, и по ним строится общая вольт-амперная характеристика всей нелинейной электрической цепи.
а) При последовательном соединении нелинейных резистивных элементов, графически заданных своими вольт-амперными характеристиками, по оси абсцисс которых откладываются напряжения, а по оси ординат – ток, складываются абсциссы этих кривых для различных значений тока. Абсцисса каждой точки эквивалентного элемента при заданном токе находится как сумма соответствующих падений напряжения на сопротивлениях, поскольку при последовательном соединении по сопротивлениям протекает один и тот же ток цепи (рис.7.5.).
Рис.7.5 К расчету электрической цепи с последовательным соединением нелинейных элементов.
Таким образом, по общей вольт-амперной характеристике
б) При параллельном соединении нелинейных резистивных элементов складываются ординаты ВАХ для различных значений напряжения. Ордината каждой точки вольт-амперной характеристики эквивалентного нелинейного сопротивления при заданном напряжении определяют как сумму токов в ветвях соответствующего сопротивления
Рис.7.6 К расчету электрической цепи с параллельным соединением нелинейных элементов.
Следовательно, при параллельном включении сопротивлений, по общей ВАХ и заданном токе источника тока, нетрудно определить падение напряжения на параллельном участке цепи, а по известному напряжению, переходя к ВАХ каждого элемента, найти ток в каждом сопротивлении. Применение графического метода расчёта цепей со смешанным соединением нелинейных резистивных элементов основано на методе свёртывания. Для получения характеристики всей цепи при смешанном соединении нелинейных элементов используются те же приемы, осуществляемые поочередно. В методе пересечения характеристик реализуется графическое решение уравнения, определяющего электрическое состояние цепи при заданной величине источника. а) При последовательном соединении линейного элемента и нелинейного резистивного элемента, графически заданного своей вольт-амперной характеристикой, решение задачи сводится к решению уравнения, составленного по второму закону Кирхгофа, и будет определяться точкой пересечения нагрузочной прямой с ВАХ нелинейного элемента. Для построения нагрузочной прямой, достаточно определить координаты двух точек, из опыта холостого хода и короткого замыкания. Напряжение холостого хода определяется по методу эквивалентного генератора. Точка пересечения линейной и нелинейной ВАХ получила название рабочей точки (рис.7.7.). По второму закону Кирхгофа:
При при
Таким образом, из графика находятся ток в цепи и напряжение на нелинейном элементе, что представляют собой координаты точки пересечения.
б) При параллельном соединении линейного и нелинейного резистивного элемента, графически заданного своей вольт-амперной характеристикой, решение задачи сводится к решению уравнения, составленного по первому закону Кирхгофа, и будет определяться точкой пересечения нагрузочной прямой. По первому закону Кирхгофа:
При IД=0 Uab = I R;
При Uab=0 IД = I.
Координаты точки пересечения двух ВАХ линейной и нелинейной являются найденным решением задачи. Они определяют ток в нелинейном элементе и напряжение на нелинейном и линейном сопротивлении (рис.7.8.).
Рис. 7.8 К расчету электрических цепей с параллельным включением нелинейного и линейного элементов методом пересечений.
Пример. Нелинейные сопротивления R1 и R2, включенные последовательно в электрическую цепь постоянного тока (рис.7.9 а), имеют вольт-амперные характеристики I и II, приведенные на рис.7.9, б. Определить ток I в цепи и напряжения U1 и U2 на этих сопротивлениях, если приложенное к цепи напряжение U = 60 В. В каких пределах измениться напряжение ΔU цепи при изменении тока I от I1 = 25 мА до I2 = 175 мА. Решение. Строят общую вольт-амперную характеристику III указанных двух последовательно соединенных нелинейных элементов (рис.7.9, б) исходя из условия, что подводимое к цепи напряжение U при данном токе I нагрузки равно сумме напряжений на сопротивлениях R1 и R2, т.е. U=U1+U2.
Рис.7.9. К расчету электрических цепей с включением нелинейных элементов
Ток в цепи при напряжении U = 60 В согласно зависимости III определяется ординатой 0 – 5, соответствующей I2 = 175 мА. Напряжение на участках цепи находят из графических зависимостей. При токе I2 = 175 мА, U1 = 19 В (абсцисса 5-4), U2 = 41 В (абсцисса 5-3). При токе I1 = 25 мА напряжение, подводимое к цепи, U = 22 В. Следовательно, изменение подводимого к цепи напряжения при изменении тока в заданных пределах согласно рис. 7.9, б составляет: ΔU = 66 – 22 = 38 В. Пример. В электрическую цепь постоянного тока (рис.7.9, в) при напряжении U = 30 В включены параллельно нелинейные сопротивления R1 и R2, вольт-амперные характеристики I и II которых представлены на рис.7.7, б. Определить общий ток I в цепи, токи I1 и I2 в ветвях. Решение. Общая вольт-амперная характеристика IV (рис.7.9, б) при параллельном соединении нелинейных сопротивлений построена сложением токов (ординат) зависимостей I и II при соответствующем напряжении. Ток нелинейного сопротивления R1 (рис.7.7, а) при заданном напряжении U = 30 В, равен, ординате 6 – 8, I2 = 100 мА. Общий ток в неразветвленной части цепи равен ординате 6 – 9 I = I1 + I2 = 205 + 100 + 305 мА. Пример. В электрическую цепь постоянного тока (рис.7.8, а) включено нелинейное сопротивление R5. Определить ток I5 в нелинейном сопротивлении и напряжение U12, действующее между точками 1 и 2 цепи. Вольт-амперная характеристика нелинейного сопротивления R5 (кривая 3) приведена на рис.7.8 б. ЭДС источника питания E = 90 В, сопротивление резисторов: R1 = 15 Ом; R2 = 45 Ом; R3 = 43 Ом; R4 = 45 Ом.
Рис.7.10. Расчет нелинейной цепи методом пересечения характеристик Решение. Используя метод эквивалентного генератора, определяем напряжение U12, действующее между точками 1 и 2 электрической цепи в режиме холостого хода при отключенном нелинейном сопротивлении R5 (рис.7.10, а). Ток в ветви резистора R1 при отключенном нелинейном сопротивлении R5 (выключатель В выключен):
Ток в ветви резистора R2 при отключенном нелинейном сопротивлении R5: ЭДС эквивалентного генератора Eэк определяют при отключенном нелинейном сопротивлении R5. По второму закону Кирхгофа из уравнения электрического равновесия, составленного для внешнего замкнутого контура электрической цепи (рис.7.10, а):
Внутреннее сопротивление Rэк эквивалентного генератора относительно точек 1 и 2 электрической цепи рис.7.8 а, при закороченном источнике ЭДС:
В соответствии со схемой замещения рассматриваемой нелинейной электрической цепи (рис.7.10, в) исходя из уравнения, составленного по второму закону Кирхгофа, имеем: Полученное уравнение представляет аналитическое выражение зависимости I5(U12). Поскольку Ток I5 в цепи нелинейного сопротивления R5 и напряжение U12 на его зажимах определяют графическим способом как координаты точек пересечения вольт-амперной характеристики нелинейного элемента R5 (рис.7.10, б) с полученной прямолинейной зависимостью I5(U12). При этом I5 = 0,45 A, U12 = 6,75 B. Пример. Для точки A вольт-амперной характеристики I(U) нелинейного элемента (рис.7.11) определить статическое Rст и дифференциальное Rд сопротивления.
Рис.7.11. Вольтамперная характеристика. Решение. Статическое сопротивление, соответствующее точке Дифференциальное сопротивление, соответствующее вольт-амперной характеристики:
ЭЛЕКТРОНИКА
Электроникой называется область технической науки, изучающая принципы действия и применение электронных приборов, которые выполняют в электрических цепях различной сложности преобразования сигнала. Работа электронных приборов основана на электрических процессах происходящих в вакууме, газах, и полупроводниковых материалах. Управление этими процессами происходит с помощью электрических и магнитных полей, температуры и освещенности. В соответствии с этим электронные приборы подразделяются на электровакуумные, полупроводниковые, фотоэлектронные, квантовые, газоразрядные приборы и т.д.
Электронные приборы Наиболее распространенным электровакуумным прибором является электронно-лучевая трубка, она остается основным узлом осциллографов, телевизионных экранов, дисплеев, мониторов и т.д. Конструкция любого электровакуумного прибора представляет собой помещенные внутри баллона (газонепроницаемой оболочки) электроды. Электродом называется проводник, эмитирующий (испускающий) - катод; или собирающий электроны (ионы) - анод; либо управляющий их движением от электрода к электроду с помощью электрического поля.
Основные электровакуумные приборы
Лампы с большим количеством электродов выполняют специальные функции и часто имеют двойное управление электронным потоком. К таким приборам можно отнести гептод - пятисеточную лампу, предназначенную для преобразования частоты. Аналогичные функции преобразования сигнала выполняют полупроводниковые приборы. Их преимущества по сравнению с лампами это – технологичность, миниатюрность, дешевизна. К недостаткам следует отнести – меньшие рабочие мощности, зависимость характеристик от внешних параметров. Работа электронных полупроводниковых приборов основана на явлении электропроводности, свойственной полупроводниковым материалам. При сплавлении двух полупроводников с различным типом проводимости, создается область раздела называемая электроно-дырочным или p-n-переходом, обладающая вентильным свойством. В отсутствии внешнего поля соблюдается равновесное состояние между диффузионным током (ток основных носителей зарядов) и током дрейфа (ток неосновных носителей заряда). Если к диоду подключить источник постоянного напряжения, плюсом к p-области, а минусом к n-области (подать прямое смещение), то равновесное состояние p-n-перехода нарушается, внешнее поле совпадает с направлением диффузионного тока, сопротивление p-n-перехода уменьшается – переход открыт. Если к p-n-переходу приложить напряжение другой полярности (обратно сместить p-n-переход), то преобладать начинает ток дрейфа, сопротивление p-n-перехода возрастает, переход закрыт. Зависимость тока от напряжения на переходе (ВАХ) имеет нелинейный, несимметричный характер рис.7.12. Р-n-переходы, а также переходы между металлом и полупроводником являются основными элементами полупроводниковых приборов, количество их определяет основные функции и особенности применения прибора. Прибор с одним p-n-переходом получил название диода. ВАХ диода совпадает с ВАХ p-n-перехода (рис.7.12). К основным параметрам диода относятся статическое и динамическое сопротивления:
Рис.7.12. ВАХ диода.
Биполярный транзистор это полупроводниковый прибор с двумя p-n-переходами, образованными тремя областями проводимостей p-n-p или n-p-n рис.7.13.
Рис.7.13. Структура биполярного транзистора
Средняя, тонкая область транзистора называется базой (б), одна крайняя область – эмиттером (э), другая крайняя область – коллектором (к). Для транзистора выполняется первый закон Кирхгофа:
В этом соотношении ток базы много меньше тока эмиттера и тока коллектора, поэтому Соотношения между токами в транзисторе характеризуется двумя параметрами: коэффициентом передачи тока эмиттера: коэффициентом передачи тока базы: Связь между коэффициентами передачи транзистора:
Полупроводниковый прибор с четырехслойной структурой n-p-n-pтипа и тремя переходами называется тиристором. Тиристор имеет три вывода – два от крайних областей и третий от слоя с дырочной проводимостью. Тиристоры малой мощности используются в схемах быстродействующих электронных выключателей, мощные – в схемах управляемых выпрямителей и устройствах управления электроприводом.
Поиск по сайту: |
 .
.
 нелинейной цепи при заданном значении напряжения Э.Д.С. легко определяют ток в нелинейной цепи I, а по заданному току, находят напряжение на каждом из последовательно соединенных сопротивлений, переходя к их вольт-амперным характеристикам.
нелинейной цепи при заданном значении напряжения Э.Д.С. легко определяют ток в нелинейной цепи I, а по заданному току, находят напряжение на каждом из последовательно соединенных сопротивлений, переходя к их вольт-амперным характеристикам. , так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение (рис.7.6).
, так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение (рис.7.6).
 ,
, ,
,  ;
; ,
,  .
.


 .
.




 .
. или
или  , откуда
, откуда  .
. .
.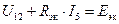 , отсюда
, отсюда  .
. и
и  , последнее уравнение является уравнением прямой в системе координат I5 и U12 (рис.7.10, б). Ee координаты определяются в режиме холостого хода – точка 1 (при I5=0; Ux=Eэк =22,5 В) и в режиме короткого замыкания - точка 2 (Uк = 0, ток
, последнее уравнение является уравнением прямой в системе координат I5 и U12 (рис.7.10, б). Ee координаты определяются в режиме холостого хода – точка 1 (при I5=0; Ux=Eэк =22,5 В) и в режиме короткого замыкания - точка 2 (Uк = 0, ток  А.
А.
 вольт-амперной характеристики:
вольт-амперной характеристики:  кОм. Статическое сопротивление пропорционально тангенсу угла a, т.е.
кОм. Статическое сопротивление пропорционально тангенсу угла a, т.е.  , где
, где  - масштаб сопротивлений.
- масштаб сопротивлений.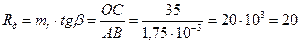 кОм. Дифференциальное сопротивление пропорционально тангенсу угла b.
кОм. Дифференциальное сопротивление пропорционально тангенсу угла b.




 .
. и
и
