и конечноэлементной моделей

Цель работы, исходные данные.

Условия задачи.

Для статически неопределимой фермы, изображенной ниже на рисунке, требуется определить перемещения и внутренние усилия в статической постановке при заданных неподвижных силовых воздействиях, определить частоты и формы собственных колебаний. Поперечные сечения всех стержней рамы одинаковы. Рама расположена в плоскости XY глобальной системы координат (рис. 1.1). Локальные координатные системы для всех стержней рамы показаны на рисунке. Локальные оси X всегда направляются вдоль стержней, направления осей y задаются в процессе генерации конечноэлементной сетки, а оси z образуют с осями x и y правую тройку.

Рис. 1.1

Физические характеристики материала рамы следующие: модуль упругости E=3×10⁶ н/м², коэффициент Пуассона m=0.2, плотность r=2500 кг/м³.

Общая информация о процессе решения задачи

Для решения поставленной задачи используется метод конечных элементов (МКЭ). Как и во всяком численном методе целью моделирования является создание качественной математической модели. Однако все решения для ее формирования принимаются на уровне разработки дискретной схемы (ДС) метода для каждой конкретной задачи, так называемой конечноэлементной модели, после описания которой в базе данных задачи вмешательство пользователя в процесс решения практически невозможно. Поскольку дискретная схема разрабатывается на основании расчетной схемы (РС), о которой в базе данных задачи предварительно следует завести информацию, носителем которой является так называемая твердотельная модель. Последняя является совокупностью геометрической модели (т.е. информации о форме и размерах) и дополненной информацией о физических и геометрических свойствах частей РС, а также о связях между ними и о воздействиях на них.

Отметим ряд технически важных деталей. При определении параметров твердотельной модели и дискретной схемы следует иметь в виду, что описание элементов всех категорий в базе данных выполняется с помощью чисел в целой или экспоненциальной формах. Комплекс PATRAN-NASTRAN фирмы MSC предоставляет относительно дружественный интерфейс, существенно облегчающий процесс представления моделей всех уровней сложности. Однако пользователь комплекса должен быть готов (до начала диалога с препроцессором) отвечать на некоторые вопросы программы именно в числовой форме.

В частности следует знать, что элемент любой категории однозначно определяется в описании любой модели своим номером, который должен быть уникальным в пределах соответствующей категории. Речь идет о номерах узлов, конечных элементов, типов конечных элементов, типов характеристик и так далее, причем не может быть, например, двух узлов, имеющих в описании одинаковый номер. То же самое касается элементов остальных категорий. В то же время допускается существование элементов разных категорий, имеющих одинаковые номера. Например, возможно существование в описании одной модели узла № 5, конечного элемента № 5, типа физических характеристик № 5 и так далее.

Предварительная проработка задачи и приемы построения твердотельной

и конечноэлементной моделей

Решения, которые предстоит принять, вырабатываются на основе анализа формы и размеров РС, а также распределения свойств и различных граничных условий в ней. Результаты анализа сопоставляются с возможностями комплекса, что позволяет сделать выводы о содержании твердотельной модели и дискретной схемы.

Работая над созданием дискретной схемы МКЭ, следует опираться на типовые конечные элементы комплекса, обеспечивающие решение поставленной задачи, то есть на библиотеку конечных элементов комплекса. В статической линейно деформируемой задаче можно использовать КЭ типа BAR. Это двухузловой (A, B) прямолинейный пространственный стержневой КЭ с постоянным поперечным сечением и шестью степенями свободы в каждом узле: тремя линейными перемещениями (TX, TY, TZ), и тремя угловыми (RX, RY, RZ) (рис. 1.4).

Заметим, что в MSC.visual NASTRAN for Windows все стержневые системы рассматриваются как пространственные, то есть отсутствуют типовые КЭ со степенями свободы только в плоскости рамы. Следует также иметь в виду, что по умолчанию КЭ жестко прикрепляются к узлам. При необходимости можно изменять количество связей в таких соединениях на уровне конечноэментной модели. Пример реализации такого приема будет рассмотрен позже.

С конечным элементом связана местная правосторонняя система координат, ось абсцисс (x) которой направлена от узла А к узлу В и совпадает с осью стержня. Оси ординат (y) и аппликат (z) в простейшем случае совпадают с главными центральными осями инерции сечения стержня в узле А.

Рис. 1.4. Конечный элемент типа BAR.

Множество геометрических характеристик сечения имеет следующий состав: As – площадь; Iy, Iz – осевые моменты инерции; Ix=Iкр – характеристика кручения; Aky, Akz – так называемые сдвиговые площади, являющиеся отношениями обычной площади As к коэффициентам сдвига при изгибе в соответствующих плоскостях (xy и xz). КЭ типа BAR допускает приложение нагрузки, распределенной вдоль оси AB по линейному закону, представляемой проекциями интенсивности на оси местной (для КЭ) или общей (для всей задачи, которая на рис. 1.4 не показана) систем координат. Именно на такие фрагменты будем мысленно делить исходную РС задачи.

Результаты описания представим в таблице 1.3. Обозначим линейные степени свободы какого-либо сечения РС символами TХ, TY, TZ, угловые степени свободы того же сечения символами RX, RY, RZ. Вторые символы обозначают оси общей системы координат, вдоль которых ориентированы векторы, представляющие соответствующие компоненты полного перемещения сечения. Так TХ означает перемещение вдоль оси Х, а RX – угловое перемещение вокруг оси Х. Символ Ä в графе таблицы 1.3 означает наличие связи в направлении соответствующей степени свободы, а отсутствие символов – отсутствие связи.

Таблица 1.3

Типовые множества связей в сечениях РС

Формализуем внешние воздействия (рис. 1.5). Опишем все типовые множества сосредоточенных сил (LP1) и распределенных нагрузок (Q1) относительно введенной общей системы координат задачи (рис. 1.5) в форме, удобной для последующего использования при работе с препроцессором. Результаты описания представим в таблице 1.4 и таблице 1.5 соответственно.

Таблица 1.4

Типовые множества сосредоточенных воздействий в РС

Проведенный анализ свойств РС позволяет пользователю принять обоснованное решение относительно количества линий, из которых будет состоять геометрическая модель. Вырабатывая такое решение нужно удовлетворить двум противоречивым условиям. Одно из них состоит в том, чтобы элементов геометрической модели было как можно меньше. Другое – чтобы как можно больше информации о свойствах РС было задано на уровне геометрической модели.

Таблица 1.5

Типовые множества распределенных воздействий в РС

Первому условию удовлетворяет решение о построении геометрической модели из трех линий: АВС, СD и FED (рис. 1.5). Из проведенного анализа следует, что можно обойтись одним типом КЭ (BAR) и одним типовым множеством свойств PR1. Если также допустить, что в этой части условия задачи меняться не будут, то характер распределения свойств не накладывает ограничений снизу на количество линий. Поскольку совокупности сосредоточенных связей расположены в местах соединений указанных линий, то характер распределения связей также не накладывает ограничений снизу на количество линий. Кроме того, следует учесть, что препроцессор MSC.visual NASTRAN for Windows не позволяет представить шарниры в сечениях B, E на уровне геометрической модели. Топология расположения распределенных воздействий в системе соответствует предложенному выше составу линий.

В данном случае на основании формы и размеров РС (рис. 1.5) можно определить состав и координаты характерных точек (Р1, Р2, Р3, Р4) геометрической модели (таблица 1.6). Ее прообраз с распределением типовых свойств, кинематических и силовых граничных условий представлен на (рис. 1.6).

Таблица 1.6

Характерные точки геометрической модели

Рис. 1.6. Прообраз геометрической модели.

При решении вопроса о количестве КЭ в задачах обсуждаемого класса можно руководствоваться критерием удобства представления результатов. Поскольку выполняемый расчет учебный, на схеме должны быть хорошо видны номера узлов и КЭ модели; очертания эпюр внутренних усилий должны корректно представлять соответствующие законы и тому подобное. Исходя из этих соображений, на горизонтальном участке без распределенной нагрузки, учитывая его большую длину (2 м), можно назначить 7 КЭ, а на вертикальных участках меньшей длины, но с равномерно распределенной нагрузкой – по 7 КЭ. Количество КЭ на каждом вертикальном участке должно быть четным, так как в серединах участков расположены шарниры. Естественно, что эти величины – ориентировочные. От них допускаются отклонения в зависимости от особенностей схем и целей расчета. Обсуждаемые параметры линий схемы, изображенной на рис. 1.6, представлены в таблице 1.7.

Таблица 1.7

Количество КЭ на линиях геометрической модели

для создаваемой конечноэлементной модели

Рис. 1.7

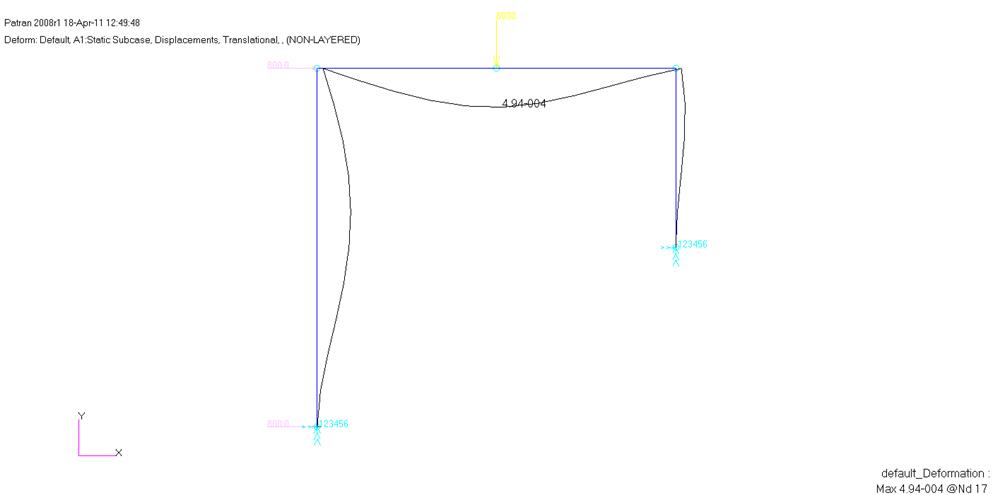
Деформированный вид:

Эпюра поперечных сил:

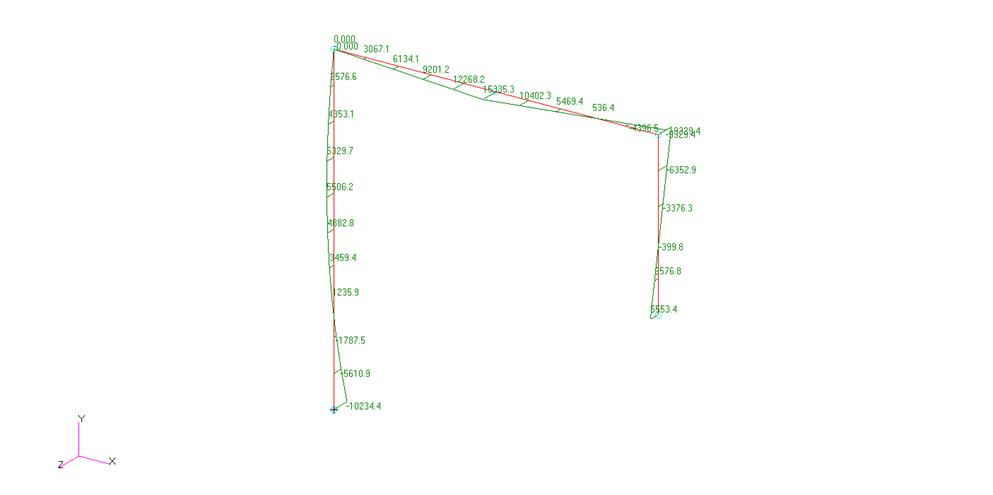
Эпюра моментов:

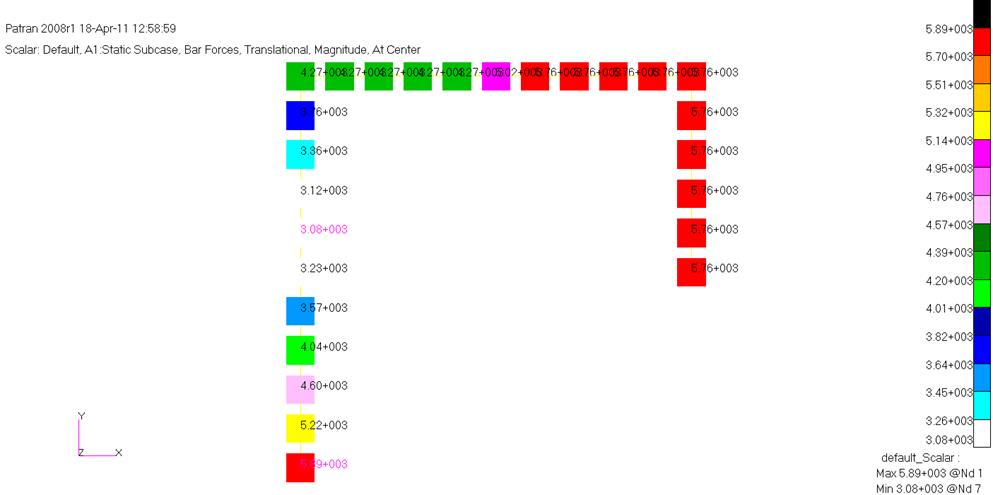
Графическое отображение законов распределения продольных сил по осям системы:

MSC.Patran 16.0.028 Sun Jun 15 15:50:12 PDT 2008 - Analysis Code: MSC.Nastran

Load Case: Default, A1:Static Subcase

Result Displacements, Translational - Layer (NON-LAYERED)

Entity: Node Vector

-Entity ID--X Component---Y Component---Z Component--

1 0.000000 0.000000 0.000000

2 0.000293 0.000000 0.000000

3 0.000986 0.000001 0.000000

4 0.001910 0.000001 0.000000

5 0.002924 0.000001 0.000000

6 0.003918 0.000001 0.000000

7 0.004807 0.000002 0.000000

8 0.005537 0.000002 0.000000

9 0.006080 0.000002 0.000000

10 0.006439 0.000003 0.000000

11 0.006645 0.000003 0.000000

12 0.006628 0.000000 0.000000

13 0.005470 0.000000 0.000000

14 0.004349 0.000000 0.000000

15 0.003300 0.000000 0.000000

16 0.002362 0.000000 0.000000

17 0.001569 0.000000 0.000000

19 0.000957 0.000000 0.000000

20 0.000512 0.000000 0.000000

21 0.000215 0.000000 0.000000

22 0.000050 0.000000 0.000000

23 0.000000 0.000000 0.000000

24 0.006645 -0.000003 0.000000

25 0.006439 -0.000003 0.000000

26 0.006080 -0.000002 0.000000

27 0.005537 -0.000002 0.000000

28 0.004807 -0.000002 0.000000

29 0.003918 -0.000001 0.000000

30 0.002924 -0.000001 0.000000

31 0.001910 -0.000001 0.000000

32 0.000986 -0.000001 0.000000

33 0.000293 -0.000000 0.000000

34 0.000000 0.000000 0.000000

36 0.006643 -0.000197 0.000000

37 0.006642 -0.000334 0.000000

38 0.006640 -0.000415 0.000000

39 0.006638 -0.000446 0.000000

40 0.006636 -0.000436 0.000000

41 0.006635 -0.000391 0.000000

42 0.006633 -0.000318 0.000000

43 0.006631 -0.000224 0.000000

44 0.006630 -0.000115 0.000000

47 0.006630 0.000115 0.000000

48 0.006631 0.000224 0.000000

49 0.006633 0.000318 0.000000

50 0.006635 0.000391 0.000000

51 0.006636 0.000436 0.000000

52 0.006638 0.000446 0.000000

53 0.006640 0.000415 0.000000

54 0.006642 0.000334 0.000000

55 0.006643 0.000197 0.000000

MSC.Patran 16.0.028 Sun Jun 15 15:50:12 PDT 2008 - Analysis Code: MSC.Nastran

Load Case: Default, A1:Static Subcase

Result Bar Forces, Translational - Layer At Center

Entity: Node Vector

-Entity ID--El. Pos. ID--X Component---Y Component---Z Component--

1 1 0.175080 0.000000 5.946387

1 2 0.175080 0.000000 5.146387

2 2 0.175080 0.000000 5.146387

2 3 0.175080 0.000000 4.346387

3 3 0.175080 0.000000 4.346387

3 4 0.175080 0.000000 3.546387

4 4 0.175080 0.000000 3.546387

4 5 0.175080 0.000000 2.746387

5 5 0.175080 0.000000 2.746387

5 6 0.175080 0.000000 1.946387

6 6 0.175080 0.000000 1.946387

6 7 0.175080 0.000000 1.146387

7 7 0.175080 0.000000 1.146387

7 8 0.175080 0.000000 0.346387

8 8 0.175080 0.000000 0.346387

8 9 0.175080 0.000000 -0.453613

9 9 0.175080 0.000000 -0.453613

9 10 0.175080 0.000000 -1.253613

10 10 0.175080 0.000000 -1.253613

10 11 0.175080 0.000000 -2.053613

11 12 0.000000 0.000000 4.107226

11 13 0.000000 0.000000 4.107226

12 13 0.000000 0.000000 4.107226

12 14 0.000000 0.000000 4.107226

13 14 0.000000 0.000000 4.107226

13 15 0.000000 0.000000 4.107226

14 15 0.000000 0.000000 4.107226

14 16 0.000000 0.000000 4.107226

15 16 0.000000 0.000000 4.107226

15 17 0.000000 0.000000 4.107226

16 17 0.000000 0.000000 -1.892774

16 19 0.000000 0.000000 -1.892774

17 19 0.000000 0.000000 -1.892774

17 20 0.000000 0.000000 -1.892774

18 20 0.000000 0.000000 -1.892774

18 21 0.000000 0.000000 -1.892774

19 21 0.000000 0.000000 -1.892774

19 22 0.000000 0.000000 -1.892774

20 22 0.000000 0.000000 -1.892774

20 23 0.000000 0.000000 -1.892774

21 24 -0.175080 0.000000 -2.053613

21 25 -0.175080 0.000000 -1.253613

22 25 -0.175080 0.000000 -1.253613

22 26 -0.175080 0.000000 -0.453613

23 26 -0.175080 0.000000 -0.453613

23 27 -0.175080 0.000000 0.346387

24 27 -0.175080 0.000000 0.346387

24 28 -0.175080 0.000000 1.146387

25 28 -0.175080 0.000000 1.146387

25 29 -0.175080 0.000000 1.946387

26 29 -0.175080 0.000000 1.946387

26 30 -0.175080 0.000000 2.746387

27 30 -0.175080 0.000000 2.746387

27 31 -0.175080 0.000000 3.546387

28 31 -0.175080 0.000000 3.546387

28 32 -0.175080 0.000000 4.346387

29 32 -0.175080 0.000000 4.346387

29 33 -0.175080 0.000000 5.146387

30 33 -0.175080 0.000000 5.146387

30 34 -0.175080 0.000000 5.946387

31 11 -2.053613 0.000000 -0.175080

31 36 -2.053613 0.000000 -0.175080

32 36 -2.053613 0.000000 -0.175080

32 37 -2.053613 0.000000 -0.175080

33 37 -2.053613 0.000000 -0.175080

33 38 -2.053613 0.000000 -0.175080

34 38 -2.053613 0.000000 -0.175080

34 39 -2.053613 0.000000 -0.175080

35 39 -2.053613 0.000000 -0.175080

35 40 -2.053613 0.000000 -0.175080

36 40 -2.053613 0.000000 -0.175080

36 41 -2.053613 0.000000 -0.175080

37 41 -2.053613 0.000000 -0.175080

37 42 -2.053613 0.000000 -0.175080

38 42 -2.053613 0.000000 -0.175080

38 43 -2.053613 0.000000 -0.175080

39 43 -2.053613 0.000000 -0.175080

39 44 -2.053613 0.000000 -0.175080

40 44 -2.053613 0.000000 -0.175080

40 12 -2.053613 0.000000 -0.175080

41 12 2.053613 0.000000 -0.175080

41 47 2.053613 0.000000 -0.175080

42 47 2.053613 0.000000 -0.175080

42 48 2.053613 0.000000 -0.175080

43 48 2.053613 0.000000 -0.175080

43 49 2.053613 0.000000 -0.175080

44 49 2.053613 0.000000 -0.175080

44 50 2.053613 0.000000 -0.175080

45 50 2.053613 0.000000 -0.175080

45 51 2.053613 0.000000 -0.175080

46 51 2.053613 0.000000 -0.175080

46 52 2.053613 0.000000 -0.175080

47 52 2.053613 0.000000 -0.175080

47 53 2.053613 0.000000 -0.175080

48 53 2.053613 0.000000 -0.175080

48 54 2.053613 0.000000 -0.175080

49 54 2.053613 0.000000 -0.175080

49 55 2.053613 0.000000 -0.175080

50 55 2.053613 0.000000 -0.175080

50 24 2.053613 0.000000 -0.175080

MSC.Patran 16.0.028 Sun Jun 15 15:50:12 PDT 2008 - Analysis Code: MSC.Nastran

Load Case: Default, A1:Static Subcase

Result Bar Forces, Rotational - Layer At Center

Entity: Node Vector

-Entity ID--El. Pos. ID--X Component---Y Component---Z Component--

1 1 0.000000 -6.735067 0.000000

1 2 0.000000 -4.516513 0.000000

2 2 0.000000 -4.516513 0.000000

2 3 0.000000 -2.617958 0.000000

3 3 0.000000 -2.617958 0.000000

3 4 0.000000 -1.039403 0.000000

4 4 0.000000 -1.039403 0.000000

4 5 0.000000 0.219151 0.000000

5 5 0.000000 0.219151 0.000000

5 6 0.000000 1.157706 0.000000

6 6 0.000000 1.157706 0.000000

6 7 0.000000 1.776261 0.000000

7 7 0.000000 1.776261 0.000000

7 8 0.000000 2.074816 0.000000

8 8 0.000000 2.074816 0.000000

8 9 0.000000 2.053370 0.000000

9 9 0.000000 2.053370 0.000000

9 10 0.000000 1.711925 0.000000

10 10 0.000000 1.711925 0.000000

10 11 0.000000 1.050480 0.000000

11 12 0.000000 -0.000000 0.000000

11 13 0.000000 1.642890 0.000000

12 13 0.000000 1.642890 0.000000

12 14 0.000000 3.285781 0.000000

13 14 0.000000 3.285781 0.000000

13 15 0.000000 4.928671 0.000000

14 15 0.000000 4.928671 0.000000

14 16 0.000000 6.571562 0.000000

15 16 0.000000 6.571562 0.000000

15 17 0.000000 8.214453 0.000000

16 17 0.000000 8.214453 0.000000

16 19 0.000000 7.457343 0.000000

17 19 0.000000 7.457343 0.000000

17 20 0.000000 6.700233 0.000000

18 20 0.000000 6.700233 0.000000

18 21 0.000000 5.943124 0.000000

19 21 0.000000 5.943124 0.000000

19 22 0.000000 5.186015 0.000000

20 22 0.000000 5.186015 0.000000

20 23 0.000000 4.428905 0.000000

21 24 0.000000 -1.050480 0.000000

21 25 0.000000 -1.711925 0.000000

22 25 0.000000 -1.711925 0.000000

22 26 0.000000 -2.053370 0.000000

23 26 0.000000 -2.053370 0.000000

23 27 0.000000 -2.074816 0.000000

24 27 0.000000 -2.074816 0.000000

24 28 0.000000 -1.776261 0.000000

25 28 0.000000 -1.776261 0.000000

25 29 0.000000 -1.157706 0.000000

26 29 0.000000 -1.157706 0.000000

26 30 0.000000 -0.219151 0.000000

27 30 0.000000 -0.219151 0.000000

27 31 0.000000 1.039403 0.000000

28 31 0.000000 1.039403 0.000000

28 32 0.000000 2.617958 0.000000

29 32 0.000000 2.617958 0.000000

29 33 0.000000 4.516513 0.000000

30 33 0.000000 4.516513 0.000000

30 34 0.000000 6.735067 0.000000

31 11 0.000000 1.050480 0.000000

31 36 0.000000 0.945432 0.000000

32 36 0.000000 0.945432 0.000000

32 37 0.000000 0.840384 0.000000

33 37 0.000000 0.840384 0.000000

33 38 0.000000 0.735336 0.000000

34 38 0.000000 0.735336 0.000000

34 39 0.000000 0.630288 0.000000

35 39 0.000000 0.630288 0.000000

35 40 0.000000 0.525240 0.000000

36 40 0.000000 0.525240 0.000000

36 41 0.000000 0.420192 0.000000

37 41 0.000000 0.420192 0.000000

37 42 0.000000 0.315144 0.000000

38 42 0.000000 0.315144 0.000000

38 43 0.000000 0.210096 0.000000

39 43 0.000000 0.210096 0.000000

39 44 0.000000 0.105048 0.000000

40 44 0.000000 0.105048 0.000000

40 12 0.000000 -0.000000 0.000000

41 12 0.000000 -0.000000 0.000000

41 47 0.000000 -0.105048 0.000000

42 47 0.000000 -0.105048 0.000000

42 48 0.000000 -0.210096 0.000000

43 48 0.000000 -0.210096 0.000000

43 49 0.000000 -0.315144 0.000000

44 49 0.000000 -0.315144 0.000000

44 50 0.000000 -0.420192 0.000000

45 50 0.000000 -0.420192 0.000000

45 51 0.000000 -0.525240 0.000000

46 51 0.000000 -0.525240 0.000000

46 52 0.000000 -0.630288 0.000000

47 52 0.000000 -0.630288 0.000000

47 53 0.000000 -0.735336 0.000000

48 53 0.000000 -0.735336 0.000000

48 54 0.000000 -0.840384 0.000000

49 54 0.000000 -0.840384 0.000000

49 55 0.000000 -0.945432 0.000000

50 55 0.000000 -0.945432 0.000000

50 24 0.000000 -1.050480 0.000000

********************************************************************************

* Beam Sections *

********************************************************************************

*UNDEFINED* 2008 r1

File: C:\sgs313katya\new ferma\ferma.db

Date: 12-May-11

Time: 09:58:29

Section Name : SEC1

Section Shape: BAR

Section Properties

------------------

Area

A = 0.012

Moments of Inertia

I1 = 1.5999999E-006

I2 = 9.0000009E-005

I12 = 0.

Torsional Constant about Centroid

J = 5.8624141E-006

Stress Recovery Points Relative to Shear Center

C1 = 0.02

C2 = 0.15000001

D1 = -0.02

D2 = 0.15000001

E1 = -0.02

E2 = -0.15000001

F1 = 0.02

F2 = -0.15000001

Shear Stiffness Factors

K1 = 0.83333331

K2 = 0.83333331

Warping Coefficient about Shear Center

CWA = 0.

Centroid Relative to Shear Center

N1A = 0.

N2A = 0.

Centroid Relative to Origin

Hori. = 0.15000001

Vert. = 0.02

Shear Center Relative to Origin

Hori. = 0.15000001

Vert. = 0.02

Angle from Axis 1 to Maximum Principal Axes

Alpha = 90.

Beam Cross Section External Perimeter

Perim = 0.68000001

Dimensions

----------

W = 0.30000001

H = 0.039999999

Поиск по сайту: