Модуляционная неустойчивость

Это явление вызвано модуляцией стационарного волнового состояния под действием нелинейных и дисперсионных эффектов. Оно проявляется, с одной стороны (во временной области), как распад непрерывной или квазинепрерывной периодической волны на последовательность сверхкоротких импульсов, с другой стороны (в частотной области), как появление двух симметричных модуляционных спектральных составляющих, отстоящих от основной (несущей) частоты w₀ на W_макс

W_макс = Ö(2×g×Р₀/½b₂½). ( 3 )

Во временной области это соответствует тому, что стационарная гармоническая волна преобразуется в периодическую последовательность импульсов с периодом Т_мод = 2p/W_макс. Явление модуляционной неустойчивости в области отрицательных дисперсий также тесно связано с возникновением солитонов.

Четырехволновое смешение

В системах WDM, использующих разные частоты w₁...,w_n в информационных каналах, зависи­мость показателя преломления от интенсивности не только вызывает ФСМ внутри канала, но и создает сигналы на новых частотах 2w_i - w_j и w_i + w_j - w_k . .

Это явление называется четырехволновым смешением (ЧВС), и в отличие от ФСМ с ФКМ, которые необходимо учитывать в системах с высокими скоростями передачи, ЧВС не зависит от скорости, а определяется величиной канальных интервалов и дисперсией волокна. При этом уменьшение канальных интервалов и дисперсии увеличивает ЧВС, в связи с чем этот эффект необходимо учитывать даже для систем с умеренными скоростями, когда каналы расположены близко друг к другу и/или используется волокно со смещенной дисперсией.

Для того, чтобы понять ЧВС, рассмотрим WDM сигнал, который представляет собой сумму n монохроматичес­ких волн

В литературе показано, что соотношение для вычисления нелинейной поляриза­ции может быть представлено в виде

Как было показано выше, первый член этого выражения отражает эффект ФСМ и ФКМ, а последующими тремя членами можно пренебречь из-за недостатка фазового синхронизма. При определенных обстоятель­ствах существует возможность приблизительного выполнения условия фазового синхронизма для оставшихся членов, все из которых имеют вид w_I + w_j - w_k , причем w_i, w_j необязательно совпадают. Если длины волн в системе WDM расположены близко друг к другу или же расположены рядом с нулевой дисперсией волокна, тогда постоянная распространения b почти постоянная величина для этих частот и условие фазового синхронизма почти вы­полняется. В этом случае мощность, генерируемая на этих частотах, может быть довольно значительной.

Таким образом, в результате нелинейности волокна возникают новые поля (вол­ны) на частоте w_i ± w_j ± w_k . Это явление называется ЧВС потому, что при объединении трех волн с частотами w_I , w_j, w_k и создается четвертая волна на частоте w_I ± w_j ± w_k . .

Существует обозначение элемента ЧВС взаимодействующих волн как w_ijk, который часто используется в литературе. Определим w_ijk = w_I + w_j - w_k, где i,j ¹ k, а также другой параметр - фактор вырождения d_ijk - d_ijk= 3 при i = j и d_ijk = 6 при i ¹ j.

Тогда элемент нелинейной поляризации на частоте w_ijk выглядит следующим образом

Если предположить, что оптический сигнал распространяется, как плоская волна в сердцевине волокна площадью S_ов, можно показать, что мощность сигнала, генерируемого на частоте w_ijk и при длине волокна L, равна

где Р_i, P_j и Р_k - мощности на входе волокна с частотами w_i, w_j и w_k, соответственно. Здесь показатель преломления n заменен эффективным показателем n_eff фундаментальной моды. Последнее соотношение можно представить в следующем виде

,

Здесь

- коэффициент нелинейности показателя преломления.

Рассмотрим числовой пример, предположив, что каждый из оптических сигналов на w_i, w_j и w_k имеет мощность 1 мВт, а эффективная область поперечного сечения волокна составляет S_eff = 50 мкм². Пусть также w_i ¹ w_j, так что d_jjk = 6 . Используя n = 3.0 ×10 ^-8 мкм²/Вт и при­нимая расстояние L =20 км, мощность P_iJk сигнала ЧВС на частоте w_jjk составит 9.5 мкВт, что только на 20 дБ ниже мощности сигнала, равного 1 мВт. Однако если в системе WDM присутствует еще один спектральный канал с частотой w_jjk, то функционирова­ние системы может существенно ухудшиться.

Для сигналов ВОСП - это представляет наихудший случай на частоте w_i]k при условии, что бит «1» был передан одновременно на частотах w_i, w_j и w_k.

На практике сигналы, генерированные ЧВС, имеют более низкие мощности вследствие неполного фазового синхронизма и потерь в волокне.

Таким образом, нелинейная поляризация приводит к взаи­модействию трех сигналов с частотами w_i, w_j и w_k. В результате возникают сигналы с частотами w_i ± w_j ± w_k, из кото­рых наибольший отрицательный эффект вызывает сигнал, соответствующий w_ijk = w_i + w_j - w_k , где i,j ¹ k.

В зависимости от комбинации частот этот «пульсирующий» сигнал мо­жет соответствовать или быть очень близким по частоте одному из информационных каналов, что приводит к значительным перекрестным поме­хам в этом канале. В многоканальных системах с N каналами это приводит к большому количеству N(N -1)² помех, при соответствующем из­менении i,j,k от 1 до N.

Явление ЧВС зависит от фазового синхронизма между взаимодействующими волнами. Если все взаимо­действующие сигналы распространяются с одной и той же групповой скоростью, что происходит при отсутствии дисперсии, это явление усиливается. С другой стороны, при наличии дисперсии различные сигна­лы распространяются с различными групповыми скоростями. Таким образом, различные волны поочередно синхронизируются и рассинхронизируются, что приводит к снижению эффекта смешения. В системах с дисперсией отличие скоростей больше, когда каналы расположены дальше друг от друга.

Для определения запаса мощности, который должна иметь система при наличии ЧВС, можно использовать последнее соотношение, которое соответствует линии связи длиной L без потерь и дис­персии

В реальных системах имеют место и потери, и дисперсия. Чтобы принять во внимание потери, заменим L эффективной длиной L_eff, ко­торая дается как

а для учета влияния дисперсии используем ко­эффициент n_ijk, который представляет эффективность смешения трех волн на частотах w_i, w_j и w_k.

Увеличения фазового рассинхронизма Db между взаимодействующими сигналами можно учесть, определив n в соотношением

где Db - разница постоянных распространения различных волн, a - коэффициент потерь. Эффективность имеет компоненту, которая периодически изменяется вдоль длины волокна по мере того, как взаи­модействующие волны совпадают или не совпадают по фазе. Отличие фаз может быть подсчитано по формуле

Db = w_i + w_j - w_k -b_ijk

где b_r - постоянная распространения на длине волны l_r.

Принимая все это во внимание, предыду­щее уравнение может быть преобразовано к виду

ЧВС проявляется в виде межканальных перекрес­тных помех, что ухудшает качество передачи информации.

Поиск по сайту:
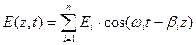