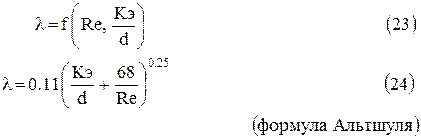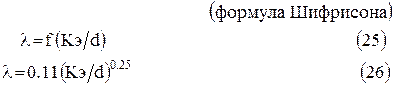|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Движение всякой вязкой жидкости по трубопроводу сопровождается потерей напора по длине, возникающей в следствие трения жидкости о стенки трубопровода, трения между слоями движущейся жидкости, а также турбулентного перемешивания. Кроме того, величина потерь зависит также от формы, размеров и шероховатости труб, а также от скорости движения и вязкости жидкости. Потеря напора - есть часть механической энергии жидкости, которая ввиду работы сил трения, распределенных по длине потока (потери по длине), а также сосредоточенных в отдельных участках потока (местные потери), переходит в тепло и необратимо теряется. Потери напора по длине hтр, для установившегося турбулентного режима движения жидкости определяется по формуле Дарси-Вейсбаха:
где hтр – потери напора; l – длина трубопровода; l – коэффициент гидравлического трения; v – средняя скорость потока; d – диаметр трубопровода. Коэффициент гидравлического трения учитывает влияние на потерю напора по длине таких факторов, которые не получили отражения в формуле Дарси - Вейсбаха в явном виде. Важнейшим из этих факторов является вязкость жидкости и состояние стенок трубы. При турбулентном режиме движения коэффициент гидравлического трения, как установлено теорией подобия, в общем случае зависит от двух безразмерных параметров числа Рейнольдса Rе и относительной шероховатости Кэ/d:
Коэффициент гидравлического трения экспериментально определится на основании соотношения, получаемого из формулы Дарси - Вейсбаха:
Таким образом, коэффициент гидравлического трения можно определить по измеренным величинам потери напора и скоростного напора на экспериментальном участке трубопровода. Внутренняя структура потока и характеристика шероховатости поверхности трубы (относительная шероховатость) обуславливают четыре типа зависимости коэффициента от числа Рейнольдса и относительной шероховатости. 1. Ламинарный режим (Rе<2300). Обтекание выступов шероховатости стенок трубы плавное, вследствие чего относительная шероховатость не влияет на величину коэффициента l. Этот коэффициент зависит только от скорости потока и определяется из соотношения
2. Гидравлически гладкие трубы (4000<Rе<105). Поток состоит из турбулентного ядра и ламинарного пристеночного подслоя. Толщина ламинарного подслоя больше среднего значения абсолютной шероховатости. Поэтому коэффициент l не зависит от относительной шероховатости, а зависит только от числа Rе.
3.Доквадратичная область (шероховатых труб) 105<Rе<500d/kэ. Толщина ламинарного подслоя соизмерима с величиной значения абсолютной шероховатости. Отдельные выступы выходят за пределы ламинарного подслоя и влияют на сопротивление движению. Коэффициент зависит как от числа Рейнольдса, так и от относительной шероховатости:
4. Квадратичная (автомодельная) область (Rе>500×d/Кэ) Развитый турбулентный режим. Толщина ламинарного слоя уменьшается по мере увеличения Rе и намного меньше среднего значения абсолютной шероховатости. Поэтому коэффициент l зависит только от относительной шероховатости Кэ/d:
Особо следует выделить область, соответствующую переходному режиму (2300<Rе<4000). Для этой области характерна перемежающая турбулентность, т.е. постоянно происходит изменение структуры потока из ламинарной в турбулентную и обратно коэффициент l можно определить по формуле Френкеля:
Поиск по сайту: |



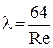 (формула Пуазейля) (21)
(формула Пуазейля) (21) (формула Блазиуса) (22)
(формула Блазиуса) (22)