 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сетевое моделирование.Стр 1 из 2Следующая ⇒
Глава 6. Сетевые модели. Моделирование сетевых структур является важной сферой для практических приложений, поскольку системы, имеющие сетевые структуры, очень широко распространены в современном мире. Достаточно упомянуть о таких жизненно важных объектах,как Интернет, сотовая связь и телефонные линии, автомобильные, железные и другие дороги, сети тепло-, водоснабжения, канализация, т. п., нефте- и газопроводы и т. д. Формализованное математическое описание систем подобного рода относится к области сетевого моделирования и основывается на теории графов. Основу научной дисциплины, называемой теорией графов, составляет совокупность методов и представлений, сформировавшихся за последние двести лет. Они включают в себя решения самых разнообразных задач таких, как движение транспорта по маршрутам, раскраска разными цветами топографических карт, нанесенных на сферу, и т. п. С тех пор, в особенности в последние два десятилетия, вследствие чрезвычайно общего характера представлений теории графов, её основные концепции нашли широчайшую сферу применения для формализованной постановки множества задач.
Сетевые структуры.
Задание сетевых структур тесно связано с частными реляционными системами, определяющимися общим выражением: g = < X, U > U Í X2, где X – сигнатура, которая состоит из бинарного или/и N-унарного отношения, называемая графом. Носитель графа Х (рис. 6.1.1,а) обычно называют множеством вершин. Сигнатуру U называют множеством дуг. Соответствующая реляционная система имеет вид: [{х1, х2, ..., х5}, {(х1, х2), (х1, х5), (х2, х5), (х4, х5), (х2, х3), (х3, х4)}].
Вершинам Vi и дугам Uj графа g = [V, U] могут быть соответственно сопоставлены (не обязательно попарно) различные элементы множеств Р и W, которые играют роль весов вершин и дуг. При этом получается взвешенный граф g = [(V, P), (U, W)] (рис. 6.1.1,б). Взвешенный граф может выступать в качестве основы для моделирования, например, системы нефтепроводов. В данном случае вершины будут представлять собой потребителей или производителей нефти, а дуги – нефтепроводы. Веса будут указывать, соответственно, на скорость потребления нефти и пропускную способность участков нефтепровода. В данном случае вес дуг графа задается расстоянием между вершинами, которые эти дуги соединяют. Если в системе имеет значение только факт связи между вершинами, то понятие дуги заменяется понятием ребра, которое геометрически изображается линией без ориентации. Без специальной оговорки под графом обычно понимается неориентированный невзвешенный граф, который также задается своими ребрами Uj и вершинами Vi,. Если граф ориентирован, то он называется ориентированным, или орграфом. При моделировании сетевых структур, также как в теории Марковских цепей и процессов, чаще всего имеют дело с орграфами, причем в последнем случае речь идет о дугах.
Рис. 6.1.1 а) ориентированный граф; (б) взвешенный граф
Дуга (ребро) графа Uj инцидентно (принадлежит) вершине Vi, а вершина Vi конинцидентна дуге (ребру) Uj, если Vi Î Uj. Вершины Vi и Vj графа g = [V, U] смежны, если {Vi, Vj} Î U. Для задания орграфов существует несколько классов матриц, основными из которых являются класс матриц инциденций и класс матриц смежности. Если орграф g содержит n вершин и m дуг, то матрица инциденций B(g) = [bij] m´n определяется как
ì 1, если вершина Vj является началом дуги Ui; bij = í –1, если вершина Vj является концом дуги Ui; î 0, если вершина Vj некоинцидентна дуге Ui;
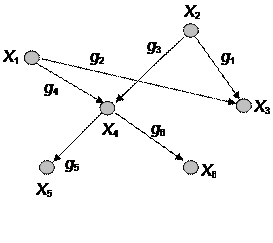
Допустим, имеется следующий ориентированный граф:
Для дуг этого графа матрица инциденций имеет вид
Для ребер этого графа матрица инциденций следующая:
Иногда орграф содержит петли, то есть дуги вида (Vi, Vi); в этом случае некоторые элементы матрицы В одновременно будут равны и 1 и –1, что приводит к неоднозначности элементов матрицы В. Для задания орграфа с петлями можно разложить матрицу В на две матрицы: В+ = [bij+]m´n, где bij+ = и В– = [bij–]m´n, где bij– =
Если орграф составлен без петель, то В = В+ – В–. Матрицы В+ и В– описывают орграф без учета весов вершин и дуг. Вес вершин орграфа g задается в виде матрицы-столбца: а веса дуг в виде диагональной матрицы порядка m:
Матрицы В+, В-, Р, W, полностью описывает взвешенный граф. Если имеется следующий орграф:
то матрица смежности для этого графа имеет вид
Матрицы A, P, W полностью описывают взвешенный орграф. Матрицы этих классов задают графы с точностью до изоморфизма. Графы g = < V, U > и g' = < V', U' > называются изоморфными, если существует такое взаимнооднозначное соответствие j между их вершинами V и V', что (Vi, Vj) Î U в том и только в том случае, если [j (Vi), j (Vj)] Î U, Vi' = j (Vi), Vj' = j (Vj). Моделируя сетевые структуры, полезно иметь понятия о различных частях графа и их некоторых свойствах. Так, вершина является самой меньшей частью графа (рис.6.1.2). Степень вершины есть число рёбер, инцидентных этой вершине: Deg(Xi) = |{Uj | Uj
Вершины орграфа вместо одной этой характеристики имеют две другие, а именно: полустепень исхода od(Xi) = | {Uj, | (Xi, Xk) = Uj}| и полустепень захода id(Xi) = |{Uj, | (Xk, Xi) = Uj}|. Окрестностью вершины Xi в графе g = <Х, U> (рис. 6.1.2) называется множество {Xj| (Xi, Xj) Î U}. Подграфом графа g = <Х, U> (рис. 6.1.2, б) называется такой граф g' = <X', U'>, в котором Х' Í Х и U' Í U . Порождённым подграфом g' = <X', U'> графа g = <X, U> называется в том случае, когда любое ребро u Î U, обе инцидентные вершины которого принадлежат Х' и U' (рис.6.1.2, в).
Также следует различать некоторые разновидности графов с экстремальными характеристиками. Простой цепью (6.1.3,а)называется граф, у которого только две вершины имеют степень, равную единице, а остальные – степень, равную двум. Цикл (6.1.3,б) есть граф, все вершины которого имеют степень, равную двум. Число вершин в цикле называется его длиной.
Рис. 6.1.3. Цепь (а) и цикл (б) в ориентированном графе.
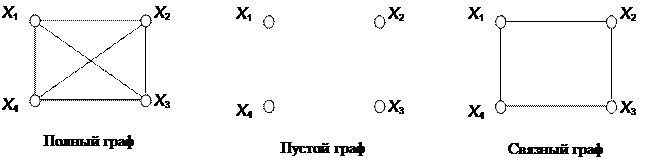
Цикл и цепь задаются последовательностью вершин и рёбер, входящих в них. Граф, все вершины которого попарно смежные, называется полным. Граф, все вершины которого попарно несмежные, называется пустым. Граф называется связным, если для любых вершин Xi, Xj существует цепь, которой принадлежат вершины Xi и Xj .
Граф может быть несвязным (а), его компонентом связности графа является подграф (б):
Связный граф на n вершинах с минимальным числом рёбер называется деревом.
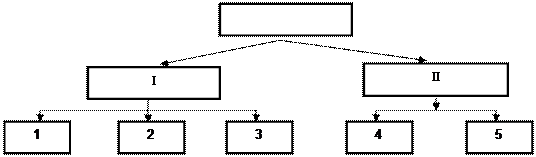
Деревья являются важной разновидностью графов и широко применяются при моделировании и построении самых различных производственных и технических систем, в том числе и вычислительных. Кроме того, построение одного особого вида дерева - дерева целей - служит одним из методов упрощения сложной системы или процесса путем их структуризации по уровням сложности. При построении дерева целей определяются функции системы, которые детализируются и конкретизируются последовательно от самой общей их формулировки до отдельного элемента системы. Такая конкретизация в графическом виде представляет собой несколько уровней сложности, каждому из которых принадлежат структурные элементы (элементы разных уровней, детализирующих какую-либо функцию системы, образуют отдельную ветвь, отсюда и название – дерево целей). При этом элементы более низких уровней обеспечивают выполнение функций на более высоких уровнях, в свою очередь, являясь целями для элементов более низкого уровня. Десагрегирование системы по уровням сложности на подсистемы производится до тех пор, пока не достигается требуемый уровень детализации. Одна из основных задач построения дерева целей – установление полного набора элементов на каждом уровне десагрегирования и определение взаимосвязей, существующих между ними. При построении дерева целей последовательно определяются: 1) принцип построения; 2) принципы детализации элементов на каждом уровне дерева; 3) глубина детализации; 4) полный набор элементов всех уровней, начиная с верхнего уровня; 5) все взаимосвязи между элементами. Дерево целей формируется на эвристической основе, при этом должны соблюдаться условия: 1) соподчиненности (элементы нижнего уровня подчиняются элементам более высокого уровня, вытекают из них, обеспечивают их реализацию); 2) сопоставимости (на каждом уровне дерева рассматриваются элементы, равноценные по своему масштабу и значимости, полученные в результате детализации, произведенной по какому-то принципу); 3) полноты (на каждом уровне представлены без пропусков все элементы); 4) определенности (формулировка целей и других элементов дает возможность оценить степень их достижения в количественной или порядковой форме); 5) возможности внесения корректировки, как при изменении самих целей, так и возможностей их реализации. В основу построения дерева целей могут быть положены два принципа: 1) целевой; 2) последовательного дезагрегирования системы. В соответствии с первым принципом на всех уровнях дерева целей представлены элементы одного и того же типа, но сформулированные с разной степенью детальности. В качестве объекта детализации в этом случае могут выступать разные уровни сложности рассматриваемой системы. При использовании второго принципа в состав дерева целей на каждом уровне включаются элементы, последовательно детализирующие и конкретизирующие функции системы, реализующиеся на первых целевых уровнях. Оба подхода к построению дерева целей не противоречат друг другу и применяются в зависимости от целей моделирования. При решении задач моделирования оба принципа могут совмещаться, например, некоторый уровень дерева целей, построенного по второму принципу, может быть подразделен на несколько подуровней, детализирующих его по целевому принципу. В зависимости от того, детализирует или нет каждый рассматриваемый элемент один или несколько элементов более высокого уровня, можно выделить три типа дерева целей. Первый тип – это дерево с прямыми связями:
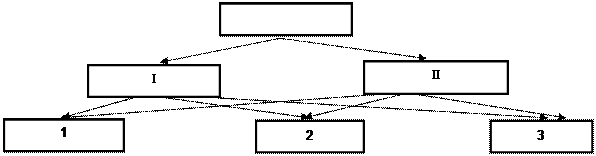
Второй тип дерева – это дерево с перекрестными связями. При перекрестных связях один и тот же элемент какого-либо уровня оказывает влияние или составляет часть сразу нескольких элементов более высокого уровня.
Дерево с перекрестными связями может быть перестроено в дерево целей с прямыми связями путем повторения одних и тех же элементов одного уровня, детализирующих разные элементы более высокого уровня. Однако для выявления полного набора элементов каждого уровня вначале лучше построить дерево с прямыми связями, а затем, если это необходимо, перейти к структуре с перекрестными связями. Помимо деревьев с прямыми связями и с перекрестными связями возможно существование деревьев со связями смешанного типа. Возможны различные принципы детализации элементов дерева целей: 1) по принципу адресности, когда тот или иной элемент конкретизируется по месту расположения в системе; 2) по объектовому принципу, когда конкретизация происходит по типу элемента; 3) по временному принципу, когда конкретизация происходит по принципу нахождения на том или ином этапе моделируемого процесса; 4) по функциональному принципу, когда конкретизация происходит согласно той или иной функции системы. Для правильного определения набора элементов, характеризующих систему, необходимо тщательно исследовать условия, в которых она функционирует, т. е. всевозможные аспекты её взаимодействия с окружающей средой. При этом, чем больше информации собрано о системе, тем лучше, естественно, при том условии, что большое количество информации не переходит в её плохое качество. Если при построении дерева целей выяснятся, что из двух соседних элементов одного уровня один служит средством достижения другого, то соответствующий элемент переводится на более низкий уровень. Если выясняется, что элементы верхних уровней не полностью отражают все системные аспекты, то вносятся дополнительные уточнения. В некоторых случаях необходимость введения дополнительного элемента на данном уровне дерева целей выявляется в процессе определения набора элементов более низкого уровня дерева. Глубина детализации (число уровней сложности системы) в основном определяется целями моделирования. Число уровней дерева зависит также от числа элементов, получаемых на отдельных уровнях. Если какой-либо элемент более высокого уровня детализируется более чем на 8-10 элементов, целесообразно, по возможности введение между этими уровнями промежуточного уровня, который агрегирует элементы более низкого уровня в меньшее количество обобщенных элементов. Такой подход в дальнейшем снижает трудности одновременной оценки большего числа элементов. Если цели моделирования не могут быть полностью выполнены в соответствии с их приоритетами с помощью выбранных способов их реализации, то должно производиться уточнение целей и путей их реализации. Например, для того, чтобы отдать предпочтение той или иной из предлагаемых технических систем, помимо общих технико-экономических характеристик системы надо знать степень её разработанности, технологичности, дефицитности, а также иметь дополнительную информацию о входящих в её состав подсистем. Предпочтительность той или иной системы определяется с учетом её влияния на элементы более высоких уровней дерева целей (оценка сверху вниз) и исходя из оценок составляющих её подсистем (оценка снизу вверх).
Сетевое моделирование.
Сетевое моделирование как раздел науки, основанной на теории графов, начиналось с решения двух наиболее известных задач: задачи о кратчайшем пути и задачи о максимальном потоке. В последнем случае, если взвешенный орграф моделирует, например, систему водопроводов, то при решении задачи о максимальном потоке воды через эту систему вершины такого орграфа представляют собой потребителей или производителей воды, а его дуги - участки водопровода. При этом веса, соответствующие каждой дуге графа, указывать на скорость потребления воды и пропускную способность труб данного водопровода. В задаче о кратчайшем пути веса дуг графа задаются расстоянием между вершинами, которые эти дуги соединяют.
Рис. 6.2.1. Топологическая карта транспортной сети из 5 ветвей
Оказывается, используя аналогию между длиной пути lij между пунктом i и пунктом j на карте и электрическим напряжением Uij между точкой i и точкой j определенной электрической цепи, можно решать задачу о кратчайшем пути, моделируя транспортную сеть Рис. 6.2.1 следующей электрической схемой:
Рис. 6.2.2. Электрическая модель транспортной сети Рис. 6.2.1
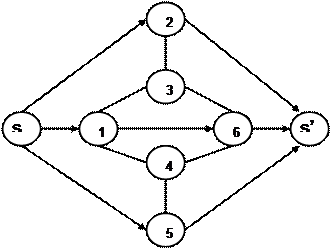
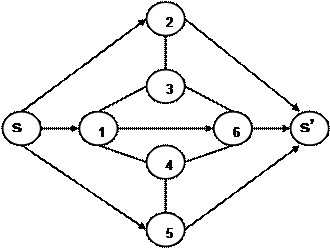
Впрочем, любая электрическая схема сама по себе представляет ориентированный и взвешенный граф. Ориентирован этот граф будет протекающими в определённых направлениях токами по разным участкам схемы. Величины токов могут играть роль весов соответствующих дуг графа, а величины напряжений - роль весов соответствующих вершин графа. Свойство постоянства потока в сети равносильно высказыванию о том, что поток в промежуточной вершине не исчезает и не возникает. Это свойство эквивалентно закону Кирхгофа для цепи постоянного тока. Для иллюстрации методов сетевого моделирования рассмотрим более подробно другую известную задачу – задачу о максимальном потоке в транспортной сети. На основе теории графов эта сеть моделируется ориентированным связным графом без петель g = [(s, P), (U, W)], который обладает следующими свойствами: 1) Существует одна и только одна такая вершина s1 называемая входом сети (источником), что g -1(s1) = 0; 2) Существует одна и только одна такая вершина sn, называемая выходом сети (стоком), что g (sn) = 0 3) Каждой дуге Uij графа соответствует некоторое число f(Uij) ≥ 0, называемое пропускной способностью дуги. Метод нахождения максимального потока рассмотрим на примере интенсивного потока автомашин, стремящихся преодолеть участок транспортной сети с односторонним движением и ограниченной пропускной способностью. Для конкретности рассмотрим участок городского движения с одним въездом на участок (s) и одним выездом из него (s'). Представим схематически модель этого участка в виде взвешенного ориентированного графа с 8 вершинами (перекрестками) и 13 дугами (переулками):
Рис. 6.2.3. Исходная сеть, исследуемая на предмет пропускной способности.
Упорядоченная пара узлов (i, j) определяет дугу этой сети, причем каждой дуге (i, j) приписывается определенная пропускная способность k(i, j). На Рис. 6.2.3 пропускная способностькаждой дуги (i, j) указана числом (автомобилей/сек) в квадратике рядом с ней. Потоком в сети называется функция f, сопоставляющая каждой дуге (i, j) число f(i, j) и обладающая свойствами:
f(i, j) = - f(j, i) ; f(i, j) < k(i, j) (6.2.1)
Пропускная способность и потокможет характеризовать как отдельную дугу, так и всю сеть. Узел s является в данном случае источником потока (автомашин) f, узел s' - стоком. Поток с одним источником s и одним стоком s' называется потоком отs кs'. Узлы s и s' связаны сложной промежуточной сетью. В соответствии с теорией графов, для удобства моделирования исходная исследуемая сеть (рис. 6.2.3) представляется симметричной матрицей пропускных способностей || k || (Табл. 6.2.1): Таблица 6.2.1.
В матрице || k || элемент i, j на пересечении строки i и столбца j соответствует пропускной способности дуги (i, j). Для начала моделирования насыщения исходной сети допустим, что из источника s в каждом из трех возможных направлений вытекает поток fsj по 1 условной единице, который в сумме дает общий поток f1 = 3. Входящие в узлы 1, 2, 5 единичные потоки должны течь дальше по сети до тех пор, пока не сольются в узле s' . Этому общему суммарному потоку величиной 3 условные единицы соответствует антисимметричная матрица потока || f1 ||. Эта матрица || f1 || вместе с ориентированным графом, соответствующим потоку f1, изображена ниже:
Знаки (-) в матрице || f1 || возникли в силу свойства (6.2.1) потока. Теперь, чтобы выяснить, насколько полно поток f1 насыщает исходную сеть, вычтем потока f1 из общей пропускной способности k, а также соответствующие этим потокам матрицы и получим новую сеть k1 = k – f1 и новую матрицу пропускных способностей || k1 || = || k || – | | f1 ||:
Появление в матрице || k1 || нулей свидетельствует о появлении насыщенных дуг, а именно дуг (s,1), (2,s') и (5,s') в результате операции вычитания. Найдем те узлы, которых можно достичь из s, следуя по ненасыщенным дугам. Эти узлы определяются положительными элементами первой строки матрицы || k1 ||, т.е. это узлы (2) и (5). Из узлов (2) и (5) достижимы узлы (3) и (4) , из узлов (3) и (4) можно попасть в узел (6), а из него - в (s'). Таким образом, одним из ненасыщенных путей является путь (s,2), (2,3), (3,6), (6,s'). Образующие этот путь элементы в матрице || k1 || обведены кружками, а элементы в квадратиках образуют путь для потока в противоположном направлении. Минимальная пропускная способность пути (s,2), (2,3), (3,6), (6,s') лимитируется дугой (2,3), значит, по нему возможен поток мощностью максимум 2 единицы. Обозначив этот поток f2 = 2, вычтем его значение из сети k1. Новую матрицу пропускных способностей || k2 || = || k1 || - || f2 || получим вычитанием 2 из элементов || k1 ||, обведенных кружками, и добавлением 2 к элементам, обведённым квадратами. Вот эта матрица || k2 ||:
Еще один ненасыщенный путь из (s) в (s’) образован дугами (s,5), (5,4), (4,6), (6,s'). Он отмечен кружками в матрице || k2 ||, а обратный путь - квадратами. Минимальное сечение этого пути лимитируется дугой (4,6) и равно 1, а значит, максимальный поток по этому пути f3 = 1. Новую матрицу пропускных способностей || k3 || = || k2 || - || f3 || получим, таким же образом, как ранее получили || k2 ||, в виде следующей таблицы:
Единственный оставшийся ненасыщенным путь из (s) в (s’) отмечен кружками в матрице ||k3||. Это путь (s,5), (5,4), (4,1), (1,6), (6,s'). Максимальный поток f4 = 1 по этому пути лимитируется дугами (4,1) и (1,6). Производя снова операцию вычитания потока f4, получим результирующую матрицу пропускных способностей ||k4|| = || k3 || - || f4 ||: Таблица 6.2.2.
Выделенные кружками узлы, которых можно достичь, исходя из (s), не включают узел (s’). Значит, сверх этого более никакой поток в исследуемой сети невозможен. Полный поток, насыщающий исходную сеть k (рис.6.2.3), слагается из найденных частичных потоков: fмакс = f1 + f2 + f3 + f4 = 3 + 2 + 1 + 1 = 7. Матрицу максимального потока || fмакс || = || k || - || k4 || получим вычитанием результирующей матрицы пропускных способностей (Табл. 6.2.2) из исходной матрицы (Табл.6.2.1):
Рис. 6.2.4. Матрица || fмакс || и соответствующий ей поток fмакс.
Полный поток, вытекающий из (s), равный сумме элементов первой строки || fмакс ||, равен полному стоку в (s’), т. е. сумме элементов последнего столбца, и оказывается равным 7 автомашин/сек. Направление потока автомашин в сети будет определяться стрелками на рис.6.2.4, а его интенсивность - числами у соответствующих дуг (переулков). Интересно отметить, что отсутствует вклад дуги (1,3) в полный поток автомашин, хотя она обладает единичной пропускной способностью (1 автомашина/сек). Таким образом, оказывается, что в этом переулке поток автомашин отсутствует (образуется пробка), несмотря на интенсивное движение в соседних переулках.
6.3. Сетевое планирование. В предыдущем параграфе объект, предназначенный для моделирования, представлялся в виде ориентированной сети. Если дуги и узлы некоторой ориентированной сети соотнести с производимыми работами и происходящими при этом событиями, то в виде сети также можно представить план работ по создание некоторого проекта. В этом случае речь идет о методе сетевого планирования - эффективном средстве реализации какого-либо проекта к заданному сроку. Иными словами, сетевое планирование есть средство планирования, руководства и контроля, применяемое для определения, согласования и увязки всех необходимых в ходе выполнения проекта составляющих этого проекта. Наглядность сетевому планированию придает сетевой график, подобный тому, который изображен на рисунке ниже.
Таким образом, сетевой график есть графическое представление в виде ориентированной сети событий и работ, входящих в данную управляемую систему. События располагаются в узлах сети, а работы выполняются вдоль дуг. Под словом работа понимается любой трудовой процесс, сопровождающийся затратами времени и ресурсов. В понятие "работа" входят: 1. Ожидание. Это пассивный процесс, не требующий трудовых и материальных затрат, но сопровождающийся потерей рабочего времени. 2. Фиктивная работа. Она отражает связь между двумя или более работами и не требует ни времени, ни ресурсов. 3. Собственно работа. Понятие "событие" означает конечный результат какой-либо работы. "Путь" в данном случае представляет собой непрерывную последовательность работ от исходного события к завершающему. В сетевом графике имеется множество путей. Путь максимальной длительности называется критическим. Для построения и расчета сетевого графика используется так называемая система PERT (Program Evaluation and Review Technique), включающая этапы: 1. Расчленение комплекса работ на определенные этапы. 2. Выявление и описание всех событий и работ. 3. Построение сети. 4. Определение времени выполнения каждой работы, 5. Определение критического пути. 6. Анализ сети и оптимизация сетевого графика. Основные правила построения графиков заключаются в следующем: 1. Каждая работа должна иметь предшествующее ей и последующее за ней событие. Каждое событие должно иметь предшествующую ему и последующую за ним работу. В противном случае наличие тупикового события свидетельствует о том, что забыта какая-то работа, выполняемая после данного события, или же предшествующая работа не нужна для завершения этого события. Исключением из этого правила являются исходное и завершающее события. Событие может иметь несколько предшествующих и последующих работ. 2. Для построения сетевого графика водятся обозначения:
а) событие б) работа в ожидании в) фиктивная работа г) критический путь
3. Недопустимо совпадение начального и конечного событий у двух и более работ, выполняемых параллельно во времени, т.е. недопустим фрагмент:
4. В случае нарушения правила № 3 вводятся дополнительные события, соединяемые фиктивными работами с одним конечным событием:
6. Ни одно событие не является свершившимся, пока не завершатся предшествующие ему работы. 7. В сети не должно быть замкнутых контуров, таких как, например:
Определение длительности работы производится следующим образом. Если нет точного определения длительности, то экспертами намечается три возможных срока выполнения работы tij: 1. Пессимистическая оценка tij=tmax. 2. Оптимистическая оценка tij=tmax. 3. Наиболее вероятная (ожидаемая) tIJ=tож. Оптимистическая оценка - это минимальное время, за которое все будет обеспечено в срок при наилучших условиях. Пессимистическая оценка - это максимальное время, за которое будет выполнена работа. Ожидаемая оценка срока определится соотношением: tож=(2tmax+3tmin)/5. Для расчета сетевого графика необходимо ввести понятия: 1. Время 2. Время 3. Время 4. Время позднего окончания работы есть самый поздний срок завершения работы. 5. Общий резерв времени представляет собой разность между поздним и ранним началом или поздним и ранним окончанием работы 6. Частный резерв времени есть разность между временем раннего начала следующей работы в ранним окончанием данной работы:
В качестве примера сетевого планирования рассмотрим следующий сетевой график некоторого гипотетического проекта длительностью Ткр=16 условных единиц: Под стрелками, представляющими работы, указаныих ожидаемые длительности в условных единицах. При расчете сетевого графика составляется таблица, в которую заносятсявсе определенные выше сроки работ и резервы времени. Для приведенного выше сетевого графика составляется следующая таблица:
Выявление работ с нулевым резервом времени в приведенной выше таблице показывает, что критический путь на данном сетевом графике определяется следующей последовательностью событий: (1)→(3)→(4)→(6). Он изображен на рисунке двойной стрелкой.
Поиск по сайту: |



 .
.
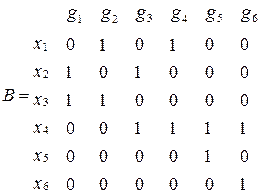 .
.

 ,
,



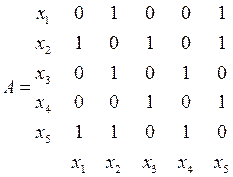 .
.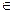 Xi}|.
Xi}|.






 Проиллюстрируем этот пример небольшой физической моделью. Пусть имеется топологическая карта сети из 5 дорог, соединяющих 4 пункта, причём необходимо выбрать кратчайший путь из пункта 1 в пункт 4:
Проиллюстрируем этот пример небольшой физической моделью. Пусть имеется топологическая карта сети из 5 дорог, соединяющих 4 пункта, причём необходимо выбрать кратчайший путь из пункта 1 в пункт 4: 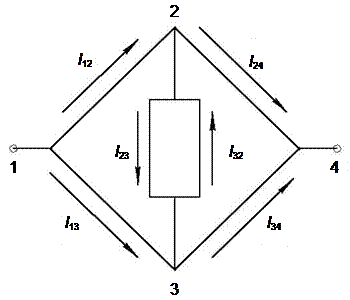

















 1
1





 3
3
 1
1
 2
2





 5. Hи одна работа не может начинаться до тех пор, пока не завершится предшествующее ей событие.
5. Hи одна работа не может начинаться до тех пор, пока не завершится предшествующее ей событие.

 2
2 1
1 3
3
 раннего начала работы (i)→(j). Это время определяется из условия, что все предваряющие события (i) работы должны быть закончены, т.е.
раннего начала работы (i)→(j). Это время определяется из условия, что все предваряющие события (i) работы должны быть закончены, т.е.  , где
, где  - путь максимальной длительности от события (1) до события (i), начального для данной работы.
- путь максимальной длительности от события (1) до события (i), начального для данной работы. раннего окончания работы:
раннего окончания работы:  . Время раннего начала и окончания работ на сетевом графике определяется для всех событий, начиная с исходного и кончая завершающим.
. Время раннего начала и окончания работ на сетевом графике определяется для всех событий, начиная с исходного и кончая завершающим. позднего начала работы (i)→(j) представляет самый поздний срок, к которому должно произойти событие (i) так, чтобы не нарушался сетевой график, т. е. должно выполняться:
позднего начала работы (i)→(j) представляет самый поздний срок, к которому должно произойти событие (i) так, чтобы не нарушался сетевой график, т. е. должно выполняться:  , где Ткр - время окончания проекта (завершающего события), а
, где Ткр - время окончания проекта (завершающего события), а  определяется как путь максимальной длины от завершающего события до события (i). Значения
определяется как путь максимальной длины от завершающего события до события (i). Значения 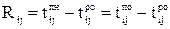 . Эта величина показывает, насколько можно передвинуть срок выполнения данных работ, не нарушая графика. Если Rij = 0, значит, работа лежит на критическом пути. Для остальных путей Rij > 0.
. Эта величина показывает, насколько можно передвинуть срок выполнения данных работ, не нарушая графика. Если Rij = 0, значит, работа лежит на критическом пути. Для остальных путей Rij > 0. . Эта величина показывает, насколько возможно продление данной работы без нарушения срока раннего начала последующей работы.
. Эта величина показывает, насколько возможно продление данной работы без нарушения срока раннего начала последующей работы.
