|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Обеспечение отказоустойчивости ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ к отказам и сбоям.
ОТКАЗОУСТОЙЧИВОСТь ВЫЧИСЛИТЕЛЬНЫх СИСТЕМ. Основные понятия отказоустойчивости вычислительных систем.
Надежность — свойство системы сохранять во времени в установленных пределах значения всех параметров, характеризующих ее способность выполнять требуемые функции в заданных режимах и условиях применения [5]. Надежность отказоустойчивых вычислительных систем (ОВС)определяется, с одной стороны, уровнем отсутствием отказов, сбоев и ошибок в их работе, с другой – возможностью быстрого восстановления работоспособности аппаратуры и вычислительного процесса в ОВС при возникновении отказов, сбоев и ошибок. Надежность зависит от назначения вычислительной системы и условий ее применения. Она представляет собой сочетание безотказности, ремонтопригодности, долговечности и сохраняемости [67].
Результатом отказов в ОВС являются систематические ошибки, приводящие к необходимости замены отказавших или использования резервных аппаратных (программных) средств восстановления аппаратуры. А результатом сбоев — случайные ошибки, вызывающие необходимость восстановления вычислительного процесса, но с использованием тех же средств. информации, искаженной ошибкой. На начальных этапах использования ОВС основное внимание уделялось вопросам обеспечения надежности аппаратных средств. По мере появления вычислительных систем чрезвычайно острой стала проблема повышения надежности программного обеспечения, поскольку ОВС, надежная для одного класса решаемых задач и одних условий эксплуатации, может оказаться недостаточно надежной для другого класса задач и других условий эксплуатации. При создании сложных ОВС именно проблема обеспечения надежности программных средств может стать критической частью по сравнению с надежностью аппаратных средств. Теория надежности сложилась как аппарат описания и исследования свойства аппаратных средств сохранять свою способность правильно функционировать во времени. Поэтому перенесение ее понятий, терминологии и методов на программное обеспечение, характеризующееся своей неизменностью во времени, не совсем правомерно. Способность программного обеспечения корректно реализовывать определенный класс задач не обязательно относить к надежности.Целесообразно было бы построить свою систему понятий и терминов и не пытаться «привязать» этот раздел теории программного обеспечения к надежности. Рассмотрим основные отличия в понятиях надежности программного обеспечения и аппаратных средств. Для аппаратных средств отказы являются событиями случайными и процедуры их восстановления практически не оказывают влияния на уровень безотказности ОВС во времени. Характеристики и причины отказов аппаратных средств, а также параметры распределения отказов во времени могут быть известны априори. Для программного обеспечения информация о возможных отказах отсутствует; при исправлении программы возможен как значительный рост, так и уменьшение уровня безотказности программного обеспечения. В этом случае статистическое распределение отказов программного обеспечения имеет существенное отличие от статистического распределения отказов аппаратных средств. Взаимодействие аппаратных средств и программного обеспечения приводит к необходимости говорить не об оценке надежности «вообще», а об оценке уровня надежности функционирования ОВС при реализации заданного класса алгоритмов в реальном масштабе времени и в определенных условиях эксплуатации. При этом необходимо учитывать сложность вычислительной системы. В классической теории надежности понятия «отказ» и «сбой» отличаются степенью физического разрушения элементов и необходимостью их ремонта или замены, причем, «сбой» устраняется «мгновенно», а отказ - «долго» [67].
B [5]приводится следующие определение «отказа системы»: Отказ — событие, заключающееся в нарушении работоспособности объекта. Как правило, отказ вызван физическим разрушением элемента ЭВМ или постепенным ухудшением ее характеристик. В [64] находим следующее определение: Сбой –это кратковременное самоустраняющееся нарушение нормального функционирования системы вследствие кратковременных воздействий на некоторый элемент внешних помех или других дестабилизирующих воздействий, а также из-за кратковременного изменения параметров элементов. После сбоя система длительное время может работать нормально. Сбой сопровождается искажением информации при операциях передачи, хранения и обработки. Следовательно, если не устранить последствия сбоя, то задача может оказаться неправильно решенной из-за искажений в данных, промежуточных результатах или в самой программе. Однако если при отказе для восстановления работоспособности необходимо устранить неисправность в аппаратуре, то при сбое достаточно восстановить только достоверность информации.
Для предупреждения неисправностей используется надежная элементная база, а также надежные средства проектирования. Однако, по мере приближения интенсивности отказов элементов к пороговым значениям, обусловленным физическими параметрами или технологией, стоимость системы резко возрастает. Применение данного подхода позволяет резко снизить интенсивность появления неисправностей, но вследствие чрезвычайно быстрого роста сложности элементов не помогает избежать всех неисправностей [64]. Целью обеспечения отказоустойчивости является возможность сохранения системой правильного функционирования при возникновении ошибок в ее программных и аппаратных компонентах [21]. Отказоустойчивыми называются системы, обеспечивающие автоматическое обнаружение ошибки, выявление ее характера (случайная или постоянная), изоляцию неисправности и реконфигурацию системы или восстановление вычислительного процесса [7]. В основе отказоустойчивых систем лежит принцип избыточности, предполагающий использование той или иной избыточности (пространственной, временной, информационной, аппаратной, алгоритмической) [28, 45, 49, 53, 55].
Зависимость надежности от времени
Наиболее распространенной статистической моделью надежности является экспоненциальная модель распределения времени до отказа, по которой вероятность безотказной работы объекта выражается зависимостью:
где λ — параметр модели.
Рис. 1.1. График зависимости вероятности безотказной работы объекта от времени для экспоненциальной модели распределения.
Экспоненциальная модель может быть использована тогда, когда интенсивность отказов величина постоянная. (Для обычного радиоэлектронного прибора это условие реализуется примерно в период эксплуатации II, если исключить период приработки I и период интенсивного старения III (рис. 1.2), а также как характеристика достаточно сложных восстанавливаемых объектов, если можно считать, что отдельные части объекта, находясь в разных стадиях износа, характеризуются в среднем постоянной функцией интенсивности) [5].
Рис. 1.2. График типичной зависимости интенсивности отказов от времени.
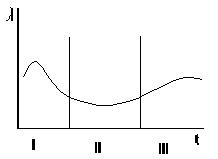
С экспоненциальной моделью тесно связана модель Пуассона, позволяющая выразить вероятность P(t, n) того, что на заданном интервале времени (0, t) произошло ровно i событий (отказов), если время между отдельными событиями (отказами) распределено экспоненциально с параметром λ. По модели Пуассона:
Модель Пуассона основана на представлении о потоке случайных событий, называемого пуассоновским, если выполнены условия стационарности, ординарности и отсутствия последействия.
В случае приближенных оценок часто используют экспоненциальную модель как наиболее удобную для аналитических преобразований. Эту модель рекомендуется применять при выполнении расчетов надежности в случае отсутствия других исходных данных для расчета, кроме интенсивности отказов λ.
Обеспечение отказоустойчивости ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ к отказам и сбоям. Обеспечение отказоустойчивости вычислительных систем к отказам и сбоям является важной проблемой при проектировании, а в конечном итоге и при эксплуатации сложных систем, функционирующих в режиме реального времени. Рассматривая отказ в качестве перманентного сбоя, далее мы ограничимся случаем возможных сбоев в работе ОВС. Важный аспект разработки ОВС – это реализация механизмов, используемых для обнаружения сбоя и обеспечения восстановления работоспособности системы. Реализация этих механизмов требует применения временной и аппаратной избыточности ОВС. Данной проблемой занимался ряд авторов [51][56] [65], которые предложили множество реализаций. Интерес последних работ в этой области состоит в поиске таких оптимальных механизмов, которые при минимальной аппаратной избыточности должны обеспечить минимальные временные потери, связанные как с контролем работоспособности системы, так и с восстановлением ее функционирования при возникновении сбоя. Известное место здесь занимают алгоритмы функционирования ОВС, когда при выполнении задания вместо одного вычислительного модуля (ВМ) используется пара или тройка ВМ, параллельно выполняющая то же задание. При помощи аппаратно или программно реализованного компаратора, сравнивающего результаты выполнения задания этими модулями, обеспечивается выявление возможных сбоев. При наличии одного или двух сбоев для пары ВМ и двух или трех сбоев для тройки ВМ для восстановления вычислительного процесса используется откат назад, т.е. повторное выполнение задания. Для оценки качества способов обеспечения ОВС естественно использовать время выполнения задания при возможных сбоях. Пусть: t– время решения задачи при отсутствии сбоев, π2 (t) – вероятность отката для пары ВМ, т.е. возникновения сбоя в одном или двух модулях за время t выполнения задания, π3 (t) – вероятность отката для тройки ВМ, т.е. возникновения сбоя в двух или трех модулях за время t выполнения задания, h ср = t * k ср - время сравнения результатов выполнения задания модулей, h отк = t * k отк - время, необходимое для обеспечения отката назад.
Тогда среднее время выполнения задания парой T2 и тройкой T3 модулей, соответственно равно:
Полагая, что функция распределения вероятностей появления сбоя подчиняется экспоненциальному распределению:
имеем
В этих условиях имеем T2Э и T3Э, которые представляют среднее время выполнения задачи для схем двух и трех ВМ соответственно:
Очевидно, для разности времени выполнения задания парой и тройкой модулей получаем:
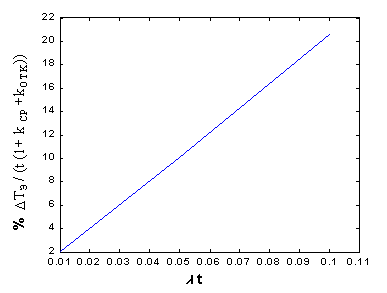
Откуда следует, что изменение значения lt от 0,01 до 0,1 приводит к изменению времени T3Э / ( t (1+ k ср + k отк ) ) от 0,03 % до 2,6 %, см. таблицу 1, и времени DTЭ / ( t (1+ k ср +k отк ) ) от 2% до 20%, см таблицу 2 и рис.1.3.
Таблица 1
Таблица 2
рис.1.3. Процент изменения времени
В [66] предлагается известный подход, уменьшающий время выполнения задания при i откатах за счет разделения времени t выполнения задания на nинтервалов длиной t/n, причем существует оптимальное значение числа интервалов n (или длины интервала t/n), при котором среднее время выполнения задания минимально. Для этого случая, очевидно, мы имеем следующее среднее время выполнения задания парой Tn2 и тройкой Tn3 модулей.
где π2(t/n) и π3(t/n) – вероятность отката при выполнении задания на одном интервале длиной t/n парой и тройкой модулей, соответственно. Для экспоненциального распределения эти выражения принимают вид:
Существует оптимальное значение числа интервалов, при которых среднее время выполнения задания минимально. В таблице 3 представлены оптимальные значения характеристик t/n, n, Tm2Э и Tm3Э при t = 1, h ср = h отс = 0,001.
Таблица 3
Таким образом, деление времени решения задания на оптимальное число интервалов значительно уменьшает среднее время выполнения задания при одном откате.
Рассмотренный критерий – среднее время выполнения задания - не является единственным. Важным показателем для систем реального времени (СРВ) является время выполнения задания при i откатах за время решения задачи. По этому критерию при lt = 0,01 время выполнения задания при одном откате составляет t (2 (1+ k ср) + k отк ) с вероятностью 0,000297 и 0,0196 (в соответствии с выражением π (1- π ) ), соответственно для трех- и двухмодульной схемы, см. также таблицу 4, где представлена вероятность выполнения задания при одном откате при различных lt. Таблица 4
При этом время выполнения задания ограничено параметром СРВ - граничным временем выполнения задания tГР. Существует качественное разграничение СРВ на жесткие и мягкие, при этом считается, что для жестких СРВ это граничное условие выполняется всегда, а для мягких СРВ выполнение условия иногда может нарушаться. Ниже мы попытаемся ввести количественное разграничение жестких и мягких СВР. Время выполнения задания t , с разделением этого времени на n интервалов при i откатах, равно:
Минимальное время выполнения задания с оптимальным числом интервалов n при i(i ≥ 1) откатах определяется условием:
Откуда находим оптимальное число интервалов:
и длину оптимального интервала времени выполнения задания:
Поэтому, минимальное время выполнения задания при i откатах имеет вид:
Вероятность того, что при выполнении задания, разделенного на nинтервалов, будет ровно iоткатов, выражается как:
Используя выражения (1) и (2), находим среднее время выполнения задачи при оптимальном числе интервалов для i откатов.
Заметим, что это время является некоторым идеальным временем, т.к. заранее неизвестно число сбоев при выполнении задачи. Для толерантных систем теперь мы можем определить жесткие СРВ i-го уровня как системы, для которых время выполнения задания с i откатами не больше граничного времени tГР, и мягкие СРВ как СРВ, для которых время tГР является граничным для среднего времени выполнения задания. Схема с тремя ВМ демонстрирует наивысшую производительность согласно критерию, который она использует как показатель среднего времени решения одной задачи, или как показатель среднего времени выполнения задания, если произошел хотя бы один сбой. Тем не менее, современные системы придают большую важность таким показателям, как размер, вес, портативность, экономный расход энергии. Поэтому появился ряд схем с дублированием вычислительного процесса, с помощью которых стараются получить производительность близкую к производительности схемы с тремя ВМ, и большую эффективность по современным показателям. Разница в производительности схем с двумя ВМ и с тремя ВМ дает те границы, в которых мы можем сравнить и оценить производительность схем с дублированием вычислительного процесса. Существует большое разнообразие таких схем, в следующей главе представлен обзор наиболее известных схем. Оценка качества этих схем уже проводилась разными исследователями [50, 51, 56, 57, 64] с большим разнообразием методов, однако необходимо проанализировать известные предложенные схемы восстановления, а также разработать универсальный метод оценки восстановления с дополнительными модулями.
Выводы
Поиск по сайту: |


 .
.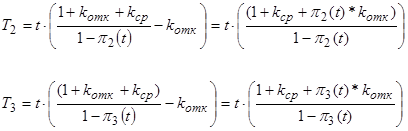

 ,
,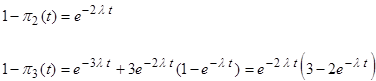
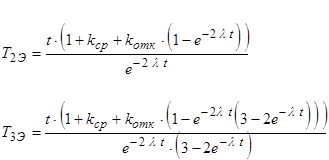
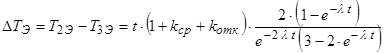 .
.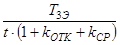
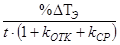

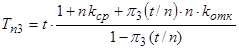

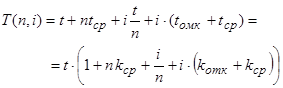
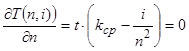
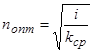
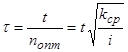
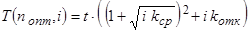 (1)
(1)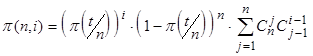 (2)
(2)