 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
V1: Элементы комбинаторикиСтр 1 из 2Следующая ⇒
V1: Теория множеств V2: Теория V3: Общая I: 1 Тема 1-1-1
S: Любая четко определенная совокупность объектов называется ### +: множеством
I: 2 Тема 1-1-1 S: Множество, которое не содержит никаких элементов, называется ### +: пустым : 5 Тема 1-1-1
I: 3 ТЗ № 112 S: Пустое множество принято обозначать: +: -: -: -: I: 4 ТЗ № 114 S: Множество В называется подмножеством множества ###, если каждый элемент множества В является элементом множества А +: А
V3: Отношения между множествами I: 5 Тема 1-1-2 S: Числовым называется множество, элементами которого являются: +: числа -: параметры -: параметры и числа -: множества
I: 6 ТЗ № 116 S: Если множество задано с помощью характеристического свойства, принята запись вида: +: -: -: -:
I: 7 ТЗ № 118 S: Если +: -: -: -: I: 8 ТЗ № 120 S: Множество +: натуральных
I: 9 ТЗ № 122 S: Множество +: целых
I: 10 ТЗ № 124 S: Если множество
-: -: +: -: I: 11 ТЗ № 125 S: Верна запись: +: -: -: -: I: 12 ТЗ № 128 S: Верна запись: +: -: -: -: I: 13 ТЗ № 131 S: Если +: -: -: -: I: 14 ТЗ № 134 S: Если множество +: -: -: -: I: 15 ТЗ № 135 S: Если +: равными
I: 16 ТЗ № 136 S: Верна запись: +: -: -: -: V3: Операции над множествами I: 17 Тема 1-1-3 S: Множество, состоящее из элементов, принадлежащих А или В называется ### двух множеств А и В +: объединением
I: 18 Тема 1-1-3 S: Множество, состоящее из элементов, которые принадлежат А иВ, называется ### двух множеств А и В +: пересечением
I: 19 ТЗ № 140 S: Если +: -: -: -: I:20 ТЗ № 141 S: Верна запись: +: -: -: -:
I: 21 ТЗ № 143 S: Если +: -: -: : I: 22 ТЗ № 144 S: Верна запись: -: +: -: -:
I: 23 ТЗ № 147 S: Если +: {2,4} -: {5} -: {3} -: {2,3,4}
I: 24 ТЗ № 149 S: Запись +: -: -: -:
I: 25 ТЗ № 151 S: При +: -: -: -: I:26 ТЗ № 153 S: Соответствие записей L1: L2: L3: L4:
L5:
R1: R2: R3: R4: R5:
I: 27 ТЗ № 154 S: Для +: -: -: -: V2: Практика I: 28 ТЗ № 171 S: Множество +: -: -: -: I: 29 ТЗ № 172 S: Множество +: -: -: -:
I: 30 ТЗ № 175 S: Множество
+: -: -: -: I: 31 ТЗ № 176 S: Множество +: -: -: -: I: 32 ТЗ № 178 S: Отношением включения « +: -: -: -: I: 33 ТЗ № 179 S: Множества +: -: -: -: I: 34 ТЗ № 180 S: Объединением множеств +: -: -: -: I: 35 ТЗ № 181 S: Для множеств +: -: -: -: I: 36 ТЗ № 182 S: Для множеств +: -: -: -: I: 37 ТЗ № 183 S: Для множеств +: -: -: -: I: 38 ТЗ № 184 S: Для множеств +: -: -: -: I: 39 ТЗ № 185 S: Для множеств +: -: -: -:
I: 40 ТЗ № 186 S: Для множеств +: -: -: -:
I: 41 ТЗ № 189 S: Равенство +: -: -: -:
I: 42 ТЗ № 190 S: Равенство +: -: -: -:
V1: Основы математического анализа V2: Теория I: 43 Тема 2-3-0 S: Последовательность, имеющая предел, называется ### +: сходящейся
I: 44 Тема 2-3-0 S: Последовательность, не имеющая предела, называется ### +: расходящейся
I: 45 Тема 2-3-0 S: Если последовательность сходится, то она имеет только один ### +: предел
I: 46 Тема 2-3-0 S: Если последовательность ###, то она ограничена +: сходится
I: 47 Тема 2-3-0 S: Переменная величина, предел которой неограниченно возрастает, называется бесконечно ### величиной +: большой
I: 48 Тема 2-3-0 S: ### постоянной величины равен постоянной величине +: Предел
I: 49 Тема 2-3-0 S: Предел ### нескольких функций равен сумме пределов этих функций +: суммы
I: 50 Тема 2-3-0 S: Предел ### нескольких функций равен разности пределов этих функций +: разности
I: 51 Тема 2-3-0 S: Предел ### нескольких функций равен произведению пределов этих функций +: произведения
I: 52 Тема 2-3-0 S: Дифференциал постоянной величины равен ### +: нулю
I: 53 Тема 2-3-0 S: Дифференциал ### равен разности дифференциалов +: разности
I: 54 ТЗ № 199 S: Если для чисел +: ограниченной
I: 55 ТЗ № 202 S: Если для последовательности +: пределом
I: 56 ТЗ № 208 S: Функция +: пределом
I: 57 ТЗ № 210 S: Первый замечательный предел имеет вид +: -: -: -: I: 58 ТЗ № 213 S: Второй замечательный предел имеет вид +: -: -: -: I: 59 ТЗ № 214 S: С помощью правила Лопиталя можно избежать неопределенности вида +: -: -: -: I: 60 ТЗ № 214 S: Дифференциал произведения вычисляется по формуле: +: -: -: -: I: 61 ТЗ № 220 S: Дифференциал частного вычисляется по формуле: +: -: -: -:
I: 62 ТЗ № 223 S: Формула интегрирования по частям имеет вид: +: -: -: -:
V2: Практика I: 63 ТЗ № 227 S: Предел +: 12 -: 90 -: 39 -: 9
I: 64 ТЗ № 228 S: Предел +: -1/2 -: 1/2 -: -2 -: 2/4
I: 65 ТЗ № 229 S: Предел -: 4 +: 6 -: 4/5 -: 8
I: 66 ТЗ № 230 S: Предел +: -: -: -: I: 67 ТЗ № 231 S: Предел +: -: -: -: I: 68 ТЗ № 232 S: Производная функции +: -: -: -:
I: 69 ТЗ № 232 S: Производная функции +: -: -: -: I: 70 ТЗ № 233 S: Производная функции +: -: -: -: I: 71 ТЗ № 233 S: Производная функции +: -: -: -:
I: 72 ТЗ № 234 S: Производная +: -: -: -:
I: 73 ТЗ № 232 S: Производная +: -: -: -:
I:74 ТЗ № 235 S: Производная функции +: -: -: -:
I:75 ТЗ № 235 S: Производная функции +: -: -: -:
I: 76 ТЗ № 237 S: Интеграл +: -: -: -: I: 77 ТЗ № 237 S: Интеграл +: -: -: -:
I: 78 ТЗ № 238 S: Интеграл +: -: -: -:
I: 79 ТЗ № 237 S: Интеграл +: -: -: -:
I: 80 ТЗ № 239 S: Интеграл +: -: -: -:
I: 81 ТЗ № 237 S: Интеграл +: -: -: -:
I: 82 ТЗ № 241 S: Производная +: -: -: -: I: 83 ТЗ № 237 S: Производная +: -: -: -:
I: 84 ТЗ № 242 S: Производная функции +: -: -: -:
I: 85 ТЗ № 237 S: Производная функции +: -: -: -:
V1: Элементы комбинаторики V2: Теория I: 86 Тема 3-5-0 S: Соединения из n элементов по m, которые отличаются либо самими элементами, либо порядком элементов, называются ### +: размещениями
I: 87 Тема 3-5-0 S: Соединения из n элементов, каждое из которых отличается лишь порядком элементов, называются ### +: перестановками
I: 88 Тема 3-5-0 S: Размещение из n элементов по n принято называть ### +: перестановкой
I: 89 Тема 3-5-0 S: Соединения из n элементов по m, которые отличаются хотя бы одним элементом, называются ### +: сочетаниями
I: 90 ТЗ № 243 S: Формула +: умножения
I: 91 ТЗ № 244 S: Формула +: сложения
I: 92 ТЗ № 246 S: Число размещений из +: -: -: -: I: 93 ТЗ № 248 S: Для размещения с повторениями из +: -: -: -: I: 94 ТЗ № 249 S: Верно равенство +: -: -: -: I: 95 ТЗ № 250 S: Число перестановок из +: -: -: -:
I: 96 ТЗ № 253 S: Для числа сочетаний из +: -: -: -: -: 97 ТЗ № 254 S: Верно равенство +: -: -: -: I: 98 ТЗ № 256 S: Формулой +: сочетаний V2: Практика I: 99 Тема 3-6-0 S: Число способов выбора из 10 студентов группы старосты, профорга и спорторга равно +: 720 -: 560 -: 120 -: 27
I: 100 Тема 3-6-0 S: Число способов выбора ручки или карандаша из 6 карандашей и 4 ручек равно +: 10 -: 54 -: 2 -: 30
I: 101 Тема 3-6-0 S: Число способов выбора 2-х студентов из 10 равно +: 45 -: 20 -: 12 -: 90
I: 102 Тема 3-6-0 S: Число способов выбора 2-х студентов на конференцию из 20 равно +: 190 -: 380 -: 40 -: 22
I: 103 Тема 3-6-0 S: Из 4-х человек вариантов построения в строй существует +: 24 -: 64 -: 256 -: 12
I: 104 Тема 3-6-0 S: Число способов перестановки букв в слове «ТЕСТЫ» равно +: 60 -: 120 -: 30 -: 70
I: 105 Тема 3-6-0 S: Число способов перестановки букв в слове «КНИГА» равно +: 120 -: 100 -: 60 -: 50
I: 106 Тема 3-6-0 S: Число способов выбора старосты курса из 3-х групп, в которых 10, 20, 15 студентов равно +: 45 -: 3000 -: 1500 -: 200
I: 107 Тема 3-6-0 S: Число способов перестановки букв в слове «ИГРА» равно +: 24 -: 48 -: 16 -: 256
I: 108 Тема 3-6-0 S: Число способов перестановки букв в слове «ШПРИЦ» равно +: 120 -: 60 -: 720 -: 360
I: 109 Тема 3-6-0 S: В четырех пробирках имеются 4 различных препарата. Их можно поставить в штатив ### способами +: 24
I: 110 Тема 3-6-0 S: Число способов проведения выборочного анализа у 2-х из 5 детей для проверки наличия инфекционного заболевания равно +: 10 -: 20 -: 12 -: 24
I: 111 ТЗ № 260 S: Различных троек, выбирая первую букву из +: 12 -: 7 -: 10 -: 15
I: 112 З № 262 S: С помощью цифр множества +: 24 -: 20 -: 6 -: 4
I: 113 ТЗ № 263 S: Из цифр множества +: 60 -: 12 -: 120 -: 30
I: 114 ТЗ № 264 S: С помощью цифр множества +: 64 -: 24 -: 9 -: 60
I: 115 ТЗ № 265 S: Из цифр +: 18 -: 8 -: 24 -: 14
I: 116 ТЗ № 266 S: Из цифр +: 36 -: 10 -: 48 -: 64
Поиск по сайту: |








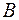 - подмножество множества
- подмножество множества 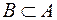



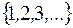 есть множество всех ### чисел
есть множество всех ### чисел есть множество всех ### чисел
есть множество всех ### чисел
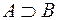







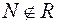




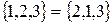

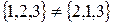

 ,
,  , то
, то




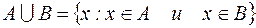
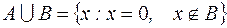

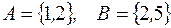 , то
, то
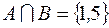
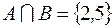





 ,
,  , то разность между
, то разность между  означает
означает

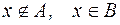

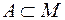 разность
разность  принято обозначать
принято обозначать

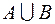
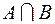




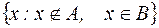

 ,
, 
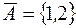



 задается перечислением:
задается перечислением:
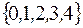
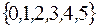

 задается перечислением:
задается перечислением:
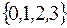
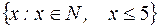
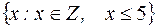


 задается перечислением
задается перечислением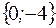








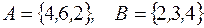


 является
является



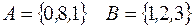 множество
множество 
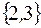

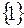
 множество
множество 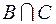 имеет вид
имеет вид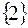


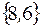
 множество
множество 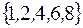

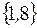

 множество
множество 


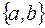
 множество
множество 
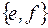


 множество
множество  имеет вид
имеет вид



 верно, если
верно, если


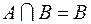 верно, если
верно, если
 при всех
при всех 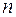 имеет место неравенство
имеет место неравенство  , то последовательность называется ###
, то последовательность называется ### существует число
существует число  приближаются как угодно близко, то это число называется ### последовательности
приближаются как угодно близко, то это число называется ### последовательности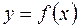 имеет своим ### величину
имеет своим ### величину  при своем приближении к
при своем приближении к  устанавливает значение функции, близкое к
устанавливает значение функции, близкое к 












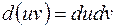










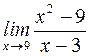 равен
равен равен
равен равен
равен равен
равен


 равен
равен

 равна
равна

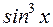

 равна
равна
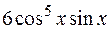
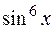

 равна
равна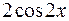
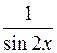


 равна
равна
 равна
равна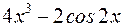

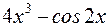

 равна
равна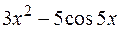



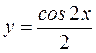 равна
равна

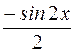

 равна
равна
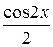
 равен
равен



 равен
равен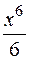


 равен
равен


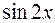
 равен
равен

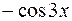

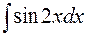 равен
равен



 равен
равен
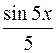


 равна
равна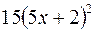


 ]
] равна
равна



 равна
равна



 равна
равна

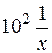

 выражает правило ###
выражает правило ### выражает правило ###
выражает правило ### определяется формулой
определяется формулой

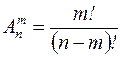



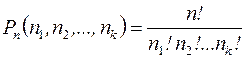
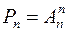













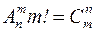
 определяется число ### из
определяется число ### из  , вторую – из
, вторую – из 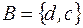 , третью – из
, третью – из  можно образовать:
можно образовать: можно записать различных трехзначных чисел:
можно записать различных трехзначных чисел: можно составить трехзначных чисел всего
можно составить трехзначных чисел всего можно составить трехзначных чисел всего
можно составить трехзначных чисел всего можно составить различных трехзначных чисел всего
можно составить различных трехзначных чисел всего можно составить трехзначных чисел всего
можно составить трехзначных чисел всего