За задание № 2 - максимальное количество - 1 балл.

Олимпиада по математике - 2015

1. Реши задачу:

В два автобуса сели 123 экскурсанта. Затем из одного автобуса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали на машине. После этого в автобусах пассажиров стало поровну. Сколько пассажиров было в каждом автобусе сначала?

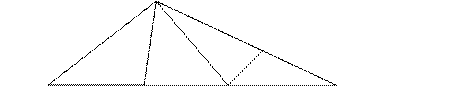
2. Сколько треугольников на чертеже?

3. Реши задачу:

Три подружки договорились купить к праздничному столу 12 пирожных. Первая купила 5 штук, вторая – 7, а третья вместо своей доли пирожных внесла 120 рублей. Как подружки должны разделить между собой эти деньги, если все пирожные были по одинаковой цене?

4. Реши задачу:

Из плохо закрытого крана за один час вытекает 150 мл воды. Какое количество людей в год можно было бы обеспечить водой, которая бесполезно вытекает из крана, если на одного человека необходимо 6 л воды в сутки?

5. Реши задачу:

В оранжерее были срезаны гвоздики: белых и розовых – 400 штук, розовых и красных – 300 штук, белых и красных – 440 штук. Сколько гвоздик каждого цвета было срезано в оранжерее?

6. Реши задачу:

На рыбалке ребята поймали 3 рыбы общей массой 3кг 250г. Две рыбы имели одинаковую массу, а масса третьей рыбки равнялась половине массы одной из двух одинаковых рыб. Найди массу каждой рыбы.

7. Реши задачу:

Два ананаса весят столько же, сколько 4 яблока, а одно яблоко – столько, сколько 3 абрикоса. На одной чаше весов – два ананаса. Сколько абрикосов надо положить на вторую чашу, чтобы весы были в равновесии?

8.Восстанови пример на сложение. Каждая буква обозначает цифру. Одинаковыми буквами обозначена одна и та же цифра.

Ответы к олимпиаде по математике - 2015

Максимальное количество баллов - - 22

1. В два автобуса сели 123 экскурсанта. Затем из одного автобуса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали на машине. После этого в автобусах пассажиров стало поровну. Сколько пассажиров было в каждом автобусе сначала?

За задание № 1 - максимальное количество - 2,5 балла.

Каждое верно выполненное действие оценивается в 0,5 балла. Принимается любое верное решение, если ученик объясняет свои действия. За отсутствие наименования в задаче снимается 0,5 балла. За отсутствие пояснений к действиям при решении задачи снимается 1 балл (кроме решения задачи уравнением или записи ее решения выражением). Если задача решена методом подбора, то ученик получает только 1 балл. Если ученик даёт только правильный ответ, а решение задачи отсутствует, то получает только 1 балл.

Решение:

1)8 – 3 = 5(чел.) – поехали в машине;

2)123 – 5 = 118(чел.) – осталось в двух автобусах;

3) 118 : 2 = 59(чел.) – стало в каждом автобусе;

4) 59 + 8 = 67(чел.) – было в первом автобусе сначала;

5) 59 – 3 = 56(чел.) - было во втором автобусе сначала;

2. Сколько треугольников на чертеже?

За задание № 2 - максимальное количество - 1 балл.

На данном чертеже 8 треугольников.

3. Три подружки договорились купить к праздничному столу 12 пирожных. Первая купила 5 штук, вторая – 7, а третья вместо своей доли пирожных внесла 120 рублей. Как подружки должны разделить между собой эти деньги, если все пирожные были по одинаковой цене?

Поиск по сайту: