 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методы классификации образов с помощью функций расстояния ⇐ ПредыдущаяСтр 3 из 3
Классификация образов сравнением с эталоном Под классификацией понимается отнесение образов к тому или иному классу. При классификации используются те или иные меры близости или сходства. В дальнейшем в качестве меры сходства используется расстояние от образа до эталона класса. В алгоритмах классификации применяется критерий минимума расстояния. Этот критерий применим как в случае единственного эталона класса, так и в случае множества эталонов. Эталоном класса называется наиболее типичный представитель образов класса. Эталоном может быть образ из выборки, представляющей данный класс, а может быть не существующий, а определенный по каким-либо правилам идеализированный образ. Классификация для единственного эталона Рассмотрим задачу определения алгоритма классификации образов для классов, представленных единственными эталонами. Целью будет служить получение решающей функции как можно более простой и эффективной. Пусть имеется
Если имеется образ Х, который необходимо классифицировать, то евклидово расстояние (между образом и эталоном) выражается формулой
Использовать расстояние как основу для построения решающей функции несколько затруднительно в силу ее нелинейности. Сформируем линейную функцию несколько преобразовав формулу расстояния. С учетом того, что расстояние – величина положительная, вместо него можно использовать его квадрат т.е.
В результате выполнения несложных преобразований с учетом того, что
не зависит от
Обозначим полученное выражение d(Х)
d(Х) = XT´Zi – 0.5´ZiT´Zi
Так как ищется минимум расстояния, то, как следует из формулы, для функции d(Х) необходимо искать максимум. Полученная формула d(Х) - это линейная функция и может быть представлена в виде:
Образ Х будет отнесён к классу
где
В итоге уравнение решающей функции может быть записано в виде
Задача классификации на множестве эталонов. Пусть теперь каждый класс
тогда функцию, определяющую расстояние между образом и эталоном класса, можно определить в виде:
Если использовать формулу для d(Х ), то решающая функция будет иметь вид
Поиск по сайту: |
 классов с единственными эталонами
классов с единственными эталонами

 :
: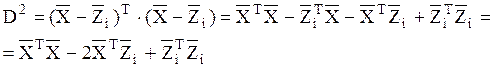


 , т.е. это слагаемое можно опустить, получим:
, т.е. это слагаемое можно опустить, получим: .
.
 , если
, если
 .
. .
. представлен множеством эталонов
представлен множеством эталонов
 .
. .
.