 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лабораторная работа №4
ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ И ЯВЛЕНИЯ РЕЗОНАНСА Цель работи - ознакомление с процессами, которые происходят в колебательном контуре, определение логарифмического декремента и добротности контура. В контуре, который содержит емкость С, индуктивность L и омическое сопротивление R, происходят затухающие колебания тока. Характеристикой затухания колебаний в контуре является логарифмический декремент затухання d, связанный з коэффиентом затухання b, условным периодом колебаний Т и условной частотой колебаний соотношениями
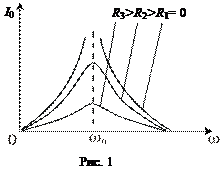
где e0-амплитудное значение ЭДС. Из (1) видно, що амплитуда силы тока максимальна при частоте вынуждающей эдс Явление резкого увеличения амплитуды силы тока при совпадении частоты собственных колебаний с частотой вынуждающей ЭДС, называется резонансом (рис.1). Если частота вынужденных колебаний постоянна, а изменяется частота собственных колебаний (при изменении L или C в контуре), то явление резонанса можно наблюдать по зависимости силы тока от индуктивности или емкости контура. С помощью таких резонансных кривых можно определить логарифмический декремент затухания и добротность контура. На рис. 2 изображена резонансная кривая, которая выражает зависимость силы тока от емкости контура при постоянной индуктивности.
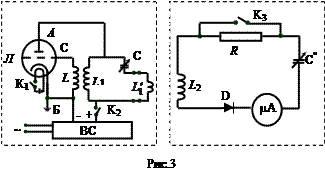
где С0 - значение емкости контура, при котором амплитуда силы тока достигает резонансного значения Ip; С1 та С2 - значения емкости, при которых амплитуда силы тока равна 0,707Ip. Для экспериментального получения резонансной кривой I=I(С) используется установка, схема которой изображена на рис.3.
Поиск по сайту: |
, 
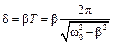где 
- частота собственных колебаний контура;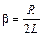 
.
Логарифмический декремент затухання d связан с другой важной характеристикой контура – его добротностью Q: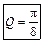 
. Для того, чтобы колебания в контуре были незатухающими, необходимо пополнять энергию колебаний. С этой целью в контур включают источник тока с ЭДС, которая изменяется по гармоническому закону. В этом случае колебания становятся незатухающими и происходят с частотой вынуждающей эдс. Амплитуда силы тока виражается соотношением
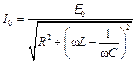, (1) (3)
.
Соответствующий расчет показывает, что логарифмический декремент затухания может быть определен по формуле
, (2)