 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные параметры сетевого графика
СЕТЕВОЕ ПЛАНИРОВАНИЕ ПРОЦЕССОВ
Методические указания к выполнению лабораторной работы по курсу “Теоретические основы автоматизированного управления” для студентов направления «Информатика и вычислительная техника» Профиль «Автоматизированные системы обработки информации и управления»
заочно-сокращенной формы обучения
Одобрено редакционно-издательским советом Саратовского государственного технического университета им. Гагарина Ю.А.
Саратов 2015 Введение
Сетью называется взвешенный ориентированный граф. Сетевые модели в настоящее время широко распространены при анализе и синтезе автоматизированных систем управления. Итак, при анализе структуры системы вначале устанавливают наличие каналов связи между теми или другими агрегатами, т. е. строят неориентированный граф, далее, учитывая направление передачи сигналов между агрегатами и их характеристиками, получают модель системы в виде сети, с которой и работают при дальнейших исследованиях. Большое распространение получили сети или сетевые графики, которые широко используются при изготовлении различных видов вычислительной техники; при построении эффективных алгоритмов функционирования систем; при изготовлении новой техники; при изготовлении и монтаже новых промышленных и гражданских зданий и сооружений, а так же при капитальном ремонте и реконструкции этих объектов. Столь широкое использование сетей делает возможным применение их в различных учебно-исследовательских работах студентов.
Цель работы: Знакомство студентов с основными способами анализа и синтеза моделей сложных систем и процессов, описываемых сетевыми графиками.
Задание 1. Предложить словесное описание какого-либо процесса и найти его целевую функцию. 2. Разбить процесс на этапы. 3. Построить сетевой график процесса и рассчитать параметры сетевого графика на ЭВМ. 4. Сделать выводы.
Основные параметры сетевого графика
Как и всякий граф, сетевой график состоит из вершин и ориентированных рёбер (дуг). Дуги изображают работы, характеризуемые некоторым параметром (весом); вершины – события, являющиеся результатом выполнения одной или нескольких работ.
Рис. 1 Пример сетевого графа
События не имеют протяжённость во времени в отличии от работ, которые имеют определённую протяжённость. Термин «работа» может иметь следующие значения: · действительная работа в прямом смысле этого слова, т. е. трудовой процесс, требующий затрат времени и ресурсов; · ожидание, не требующее затрат труда, но занимающее некоторое время (например, процесс затвердевания бетона); · фиктивная работа, не требующая ни затрат времени, ни ресурсов, но указывающая, что возможность начала одной работы непосредственно зависит от результатов другой работы. Обычно, на сетевых графиках действительные работы изображают сплошными линиями; фиктивные – пунктирными. В силу ацикличности сетевого графика, существует по крайне мере одно исходное и одно завершающее событие. Необходимым и достаточным условием начала любой работы, кроме начальной, является окончание всех предшествующих ей работ (например, начало работы (10, 11) возможно после окончания работ (2, 10) и (7, 10) – рис. 1). Определение исходного события представляет собой формулировку условий для начала работ по выполнению данного комплекса операций. Исходное событие не является следствием или результатом выполнения ни одной из работ, входящих в данный сетевой график, поэтому у этой вершины нет ни одной входящих дуг. Завершающее событие представляет собой формулировку цели данного комплекса работ. Оно не служит условием начала ни одной из работ, входящих в данные сетевой график. Из этой вершины не выходит ни одной дуги, т. к если цель достигнута, то нет смысла продолжать работу. При построении сетевых графиков необходимо соблюдать следующие правила: 1. Не должно быть тупиков, т. е. событий, из которых не выходит ни одной работы, если только это событие не является завершающим. 2. Не должно быть событий, в которые не входит ни одной работы, если только это событие не является исходным. 3. В сети не должно быть замкнутых контуров. 4. В сети не должно быть одинаковых работ, т. е. не должно быть параллельных дуг. Сумма весов дуг, участвующих в образовании пути (маршрута, где все вершины различны) называется продолжительностью пути. Например, продолжительность различных путей (Lk) сетевого графика (рис. 1) приведены в таблице 1. Таблица 1.
Путь, имеющий наибольшую продолжительность, называется критическим (Lкр). В сети может быть несколько критических путей. Длительность критического пути (tкр) определяет общую продолжительность работ (например, в табл. 1: L5=Lкр: tкр=170. Разница между продолжительностью критического пути tкр и любого другого пути сети t(Lк) называется полным резервом времени пути и обозначается P(Lk). P(Lk)=tкр-t(Lk). Величина P(Lk) показывает, на сколько в сумме может быть увеличена продолжительность всех работ, принадлежащих (Lk), чтобы при этом не изменилась продолжительность критического пути. Для любого события (i) сетевая модель позволяет определить наиболее ранний срок его свершения из возможных tp(i) и наиболее поздний tn(i) из допустимых. Ранний срок свершения любого события (i) равен сумме продолжительности работ, лежащих на максимальном из путей, ведущих к данному событию из исходного события сети. Обозначив максимальный, предшествующий событию (i) путь через L(I tp(i)=t[L(I например, tp(5)=t[L(I Поздний срок свершения любого события (i), tn(i), равен разности между продолжительностью критического пути и суммарной продолжительностью работ, лежащих на максимальном из путей, ведущих от данного события к завершающему событию сети. Обозначив максимальный из следующих за событием I путей через L(i tn(i)=tкр-t[L(I например, tn(5)=170-t[L(5 Резерв времени события (i) определяется как разница между поздним и ранним сроком свершения события и обозначается
например, Резерв времени события показывает, на какой предельно допустимый период времени можно задержать свершение этого события, не вызывая при этом увеличение tкр. События критического пути не имеют резерва времени, т. к. у них tn(i)=tp(i) Используя tn(i) и tp(i) всех событий сети можно для любой работы определить 1. ранний срок начала tрн(i,j); 2. ранний срок окончания tро(i,j); 3. поздний срок начала tпн(i,j); 4. поздний срок окончания tпо(i,j);
по формулам: tрн(i,j)=tр(i); tпн(i,j)= tп(j)-t(i,j); tро(i,j)= tр(j)+t(i,j); tпо(i,j)=tn(j); Для всех работ критического пути: tрн(i,j)=tпн(i,j); tро(i,j)=tпо(i,j). Одним из центральных понятий является понятие полного резерва времени работы входящей в сетевую модель. Различают три вида резервов времени работы: полный и два вида частных. Полным резервом времени работы (i,j) называется резерв времени, равный величине резерва времени максимального из путей, проходящих через данную работу. Обозначается полный резерв работы Rn(i,j). Для работы критического пути Rn(i,j)=0. Для остальных работ, величина Rn(i,j) определяется формулой: Rn(i,j)= tn(j)- tp(j)-t(i,j); например, Rn(5,12)= 160-70-40=50. Частный резерв времени первого вида R1 n(i,j) показывает какая часть полного резерва времени работы (i,j) может быть использована для увеличения её продолжительности при условии, что это увеличение не вызовет изменение позднего срока свершения её начального события и следовательно, сокращения резервов времени ни у одной из предшествующих этому событию работ. Частный резерв первого вида вычисляется по формуле: R1 n(i,j)= tn(j)- tn(j)-t(i,j); например, R1 n(5,12)=160-100-40=20. Частный резерв второго вида R11 n(i,j) или свободный резерв времени – это максимальное количество времени, на которое можно увеличить продолжительность работы или отсрочить её начало, не изменяя при этом ранних сроков начала последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок. R11 n(i,j)= tp(j)- tp(j)-t(i,j); например, R11 n(5,12)=110-70-40=0. Для определения «узких мест» графика, т. е. тех работ, на которых следует сосредоточить основное внимание, недостаточно знать лишь резервы времени. Более полной характеристикой степени трудности выполнения работ служит коэффициент напряжённости работы Кн(i,j). Он равен отношению продолжительностей несовпадающих (заключённых между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим - критический путь.
Здесь t1(Lкр) – сумма весов дуг максимального пути совпадающих с критическим путём; t(Lmax) –сумма весов дуг максимального пути, проходящего через работу (i,j). С учётом ранее приведённых формул:
например, Кн(5,12)=1-50/170=0,71 Чем выше коэффициент напряжённости, тем сложнее выполнять данную работу. Величина Кн(i,j) заключена внутри отрезка [0,1]. Работ критического пути Кн(i,j)=1. Коэффициент напряжённости используется при анализе и контроле физического состояния работ, позволяет выявлять все работы, требующие особого внимания руководителя. По значениям коэффициента напряжённости все работы сети могут быть разбиты на следующие зоны: 1. критическая зона – работы, имеющие значения Кн(i,j) 2. зону резерва, объединяющую работы, для которых Кн(i,j) 3. промежуточная зона, к которой относятся работы с коэффициентом напряжённости, лежащим в пределах (0,5 Перераспределение ресурсов внутри сетевого графика должно идти, как правило, в одном направлении: из зон менее напряжённых к зонам более напряжённым. Чем меньше будет объём критической и резервной зон, тем лучше синтезирована модель процесса, описываемого сетевым графиком.
Поиск по сайту: |

 , получим:
, получим: ]=t[L(0,1,4,5)]=70.
]=t[L(0,1,4,5)]=70. C), получим
C), получим ],
],
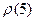 =30дней
=30дней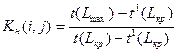

 0,8
0,8