 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Краткое теоретическое введение.
Изучение колебаний пружинного маятника. Методические указания к выполнению лабораторной работы № 16 по разделу “Механика” для студентов инженерно - технических специальностей всех форм обучения
Курск 2005
Составитель: А.Н. Лазарев
УДК 53 Рецензент
Канд. физ.- мат. наук, доцент Е.В. Пьянков
Изучение колебаний пружинного маятника.[Текст]: методические указания к выполнению лабораторной работы №16 по разделу "Механика" /сост.:/А.Н.Лазарев; Курск. гос. техн. у-т.; 2005 11 с. Ил. 1 табл. 3 библиогр.назв. 6.
Излагаются методические рекомендации по выполнению заданий лабораторной работы № 16 по разделу "Механика". Методические указания соответствуют требованиям ГОС и программе по физике утвержденной учебно-методическим советом для специальностей технического направления.
Методические указания предназначены для студентов всех инженерно – технических специальностей.
Текст печатается в авторской редакции.
ИД № 06430 от 10.12.01. Подписано в печать . Формат 60х84 1/16. Печать офсетная. Усл. печ. л. .Уч.-изд. л. . Тираж 50 экз. Заказ Бесплатно . Курский государственный технический университет. Издательско–полиграфический центр Курского государственного технического университета: 305040, Курск, ул. 50 лет Октября,94.
Лабораторная работа № 16 Изучение колебаний пружинного маятника.
Цель работы: исследовать зависимость периода колебаний и коэффициента затухания колебаний пружинного маятника от его массы. Приборы и принадлежности: пружинный маятник, набор грузов, секундомер.
Краткое теоретическое введение. Колебания – это периодически повторяющийся во времени процесс. Если колебательная система (иначе иногда называют осциллятором) идеальна, т. е. в ней не происходит диссипация энергии, то колебания не затухают. В реальных колебательных системах колебания не будут затухать только в том случае, если рассеянная в процессе колебания энергия системы пополняется за счет внешнего источника. Это автоколебания или вынужденные колебания. Гармоническими называют колебания, которые описываются периодическими функциями синус или косинус
Количественно колебания характеризуются следующими параметрами. Период колебаний T -время, за котороесовершается одно полное колебание. Частота колебаний n - число полных колебаний за единицу времени. n = Амплитуда А - это наибольшее значение периодически изменяющегося параметра колебательной системы. Круговая или циклическая частота
Фазой колебаний называют аргумент синуса или косинуса.
Это комплексный параметр колебательной системы, который определяется свойствами самой колебательной системы - Пружинный маятник представляет собой груз, подвешенный на пружине. В состоянии равновесия консервативная сила тяжести
Взяв за начало отсчета положение равновесия растянутой пружины, мы в дальнейших рассуждениях не будем учитывать силу тяжести и начальное растяжение пружины. По закону Гука сила упругости
где: При отклонении груза от положения равновесия на него будет действовать сила упругости, и второй закона Ньютона для груза будет иметь вид:
где:
Переходя к проекциям сил и смешений на вертикальную ось, получим дифференциальное уравнение гармонических колебаний:
Его решение имеет вид:
Груз совершает колебания с частотой
и периодом
Выражения (11), (12), (13) выведены без учета массы пружины
Уравнение движения груза (10) и его решение (14) описывают незатухающие колебания пружинного маятника, происходящие под действием консервативных сил. Такие колебания могут совершаться сколь угодно долго без потери механической энергии. Если на колебательную систему действует диссипативная сила сопротивления, то механическая энергия системы убывает, а колебания затухают. Силы сопротивления довольно сложно зависят от скорости, но в простейших случаях можно считать, что сила сопротивления пропорциональна скорости движения. Тогда уравнение движения груза, колеблющегося на невесомой пружине, в проекциях на вертикальную ось будет:
где F= - Решение этого уравнения имеет вид:
где:
Амплитуда колебаний -
убывает со временем по экспоненциальному закону, поэтому колебания называют затухающими, а b – коэффициент затухания, характеризует быстроту уменьшения амплитуды колебаний. Его физический смысл ясен из следующих рассуждений. Пусть
При
Натуральный логарифм отношения этих амплитуд будет равен:
ln
Если Коэффициент затухания b- это физическая величина, характеризующая затухание колебаний и численно равная натуральному логарифму отношения двух амплитуд, измеренных в моменты времени, отличающиеся на одну секунду. Если измерить промежуток времени - Если моменты времени отличаются на период, то
где: l - логарифмический декремент затухания.
Временем релаксации -
За время
Логарифмический декремент затухания колебаний это величина обратная числу колебаний, за которые амплитуда уменьшается в
Описание установки.
Установка для изучения колебаний пружинного маятника представляет собой пружину с платформой для грузов и указателем для определения удлинения пружины. Платформа с трением перемешается по вертикальным направляющим. Указатель перемещается вдоль линейки, что позволяет измерять удлинение пружины и амплитуду колебаний.
Задание1. Определить коэффициент жесткости пружины. Записать показание указателя положения платформы без груза и, нагружая платформу разными грузами и их комбинациями (не менее 5), определить в каждом случае удлинение пружины. Сила упругости F равна по величине силе тяжести груза mg. Построить график зависимости удлинения пружины от действующей на нее силы
По тангенсу угла наклона прямой к оси ОХ, определить коэффициент жесткости пружины
Задание 2. Исследовать зависимость периода колебаний пружинного маятника от его массы. Для этого на платформу маятника положить поочередно 5-10 грузов или их комбинаций. Определить время (не менее трех раз) 5-10 колебаний. Экспериментальный период определить, разделив среднее время на число колебаний. Для этих же грузов рассчитать период по формуле:
где: Построить графики зависимостей
Задание 3. Исследовать зависимость коэффициента затухания
Рекомендуемые таблицы.
Опыт 1:
Опыт 2.
Опыт 3.
Контрольные вопросы.
1. Дать определение гармонических колебаний и величин их характеризующих. 2. Вывести уравнение гармонических незатухающих и затухающих колебаний. Показать что функции:
являются решениями соответствующих уравнений. 3. Определить величины характеризующие затухание колебаний: коэффициент затухания, логарифмический декремент затухания, время релаксации колебаний. Вывести формулы взаимосвязи между ними. 4. Изучить принцип работы устройств, предназначенных для гашения нежелательных колебаний – демпферов, амортизаторов. 5. Записать формулы для определения кинетической, потенциальной и полной энергии пружинного маятника.
Поиск по сайту: |
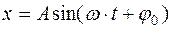 , (1)
, (1) .
. . (2)
. (2) - это величина, связанная с линейной частотой n соотношением
- это величина, связанная с линейной частотой n соотношением . (3)
. (3) . (4)
. (4) и временем - t.
и временем - t.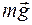 , действующая на груз, уравновешивается силой упругости
, действующая на груз, уравновешивается силой упругости 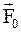 растянутой пружины
растянутой пружины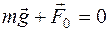 . (5)
. (5) пропорциональна удлинению
пропорциональна удлинению 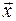 .
. , (6)
, (6) - коэффициент жесткости пружины, минус в формуле указывает на то, что вектор удлинения пружины
- коэффициент жесткости пружины, минус в формуле указывает на то, что вектор удлинения пружины 
 , (7)
, (7)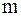 – масса груза.
– масса груза. . (8)
. (8) . (9)
. (9)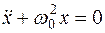 . (10)
. (10)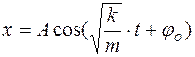
 . (11)
. (11) , (12)
, (12) . (13)
. (13)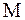 . С ее учетом решение примет вид:
. С ее учетом решение примет вид: . (14)
. (14)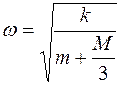 ;
;  . (15)
. (15) , (16)
, (16) – сила сопротивления,
– сила сопротивления,  - коэффициент сопротивления, а минус указывает на то, что сила сопротивления направлена против скорости.
- коэффициент сопротивления, а минус указывает на то, что сила сопротивления направлена против скорости.
 , (17)
, (17)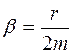 ,
,  , (18)
, (18) , (19)
, (19) , тогда амплитуда в этот момент времени равна:
, тогда амплитуда в этот момент времени равна: ,
,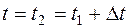 ,
, .
. . (20)
. (20) , то
, то  (1/с).
(1/с). , за который амплитуда уменьшится в 2 раза, то ln
, за который амплитуда уменьшится в 2 раза, то ln  и
и  . Это выражение используется для экспериментального определения коэффициента затухания.
. Это выражение используется для экспериментального определения коэффициента затухания. , (21)
, (21) затухающих колебаний называют промежуток времени, за который амплитуда колебаний уменьшается в
затухающих колебаний называют промежуток времени, за который амплитуда колебаний уменьшается в 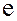 =2.71 раз.
=2.71 раз. , (22)
, (22) (23)
(23) система совершает число колебаний равное
система совершает число колебаний равное , (24)
, (24)
 ,
,  . (25)
. (25) =2.71 раз.
=2.71 раз.

 .
. ,
,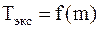 ,
,  и сделать вывод о совпадении, или отличии характера этих зависимостей.
и сделать вывод о совпадении, или отличии характера этих зависимостей. колебаний пружинного маятника от его массы. Для каждого значения массы маятника измерить время
колебаний пружинного маятника от его массы. Для каждого значения массы маятника измерить время  (не менее 5 раз) за которое амплитуда колебаний маятника уменьшается в 2 раза. Вычислить среднее его значение и определить коэффициент затухания по формуле
(не менее 5 раз) за которое амплитуда колебаний маятника уменьшается в 2 раза. Вычислить среднее его значение и определить коэффициент затухания по формуле 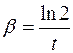 . Опыт повторить 5-7 раз, используя грузы различной массы. Построить график зависимости
. Опыт повторить 5-7 раз, используя грузы различной массы. Построить график зависимости  и сделать вывод о ее характере.
и сделать вывод о ее характере. ,
,