 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема: Оценка достоверности результатов эксперимента с помощью критерия Пирсона
ОЦЕНКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ С ПОМОЩЬЮ КРИТЕРИЯ ПИРСОНА
Лабораторная работа №5 Тема: Оценка достоверности результатов эксперимента с помощью критерия Пирсона Цель работы: ознакомление и приобретение навыков статической обработки результатов экспериментальных данных в судостроении Задача: выполнить статическую обработку экспериментальных данных, полученных в лабораторной работе №1 методом Пирсона. Для чего: 1. Преобразовать совокупность замеров fi в статический ряд, сгруппировав одинаковые замеры; 2. Определить математическое ожидание 3. Определить дисперсию (степень рассеяния величины f ) Краткая теория: Пусть на основе опытов, в которых проведено n независимых замеров величины, получена совокупность замеров x1, x2,,x3,…,xn. Оценку достоверности результатов можно выполнить с помощью критериев согласия, в частности, критерия Пирсона [2]. Критерий x2 Пирсона представляет собой величину: x2= где ni – число замеров отвечающих данному принятому диапазону изменений величины x; αi - вероятность числа замеров в соответствии с гипотетическим распределением; k - число разрядов (диапазонов или участков с k = 1, 2, 3, 4… раза попадания в них одинаковых значений fi); n - общее число замеров. Суть метода: выдвигается гипотеза, что случайная величина имеет ряд распределения xi…xn согласно принятому гипотетическому, а отклонения наблюдаемых частот замеров от гипотетического обусловлены случайными причинами; оценка достоверности такой гипотезы проводится после подсчета критерия x2 по данным табличного распределения (см. абл. 5) для определения уровня значимости P; считается, что при уровне значимости более 7% опытные данные практически не противоречат высказанной гипотезе, при этом полученное среднеарифметическое (математическое ожидание)
Ход работы: Применение критерия Пирсона для статистической обработки экспериментальных данных замеров коэффициента трения f швартова о кнехт выполняется в последовательности: 1. Произвести выборку замеров fi из лабораторной работы № 1, результаты выборки внести в таблицу 1; 2. Преобразуем совокупность замеров fi из таблицы 1 в следующий статистический ряд, сгруппировав их одинаковые замеры; данные обработки внести в таблицу 2, где fi = f1, f2, f3, f4 – значения одинаковых замеров fi; k = 1,2,3,4,… – число, показывающее сколько раз встречается одинаковое значение замеров fi в таблице 1 выборки. 3. Определить математическое ожидание статистического распределения величины f по данным таблицы 2 [1].
4. Определить дисперсию Df (рассеяние значений fi):
5. Выскажем следующую гипотезу: статистическое (случайное) распределение замеров fi подчинено нормальному закону распределения Гаусса с параметрами (5.2) и (5.3), а следовательно, носит случайный характер. 6. Преобразуем статистический ряд (таблица 2), составив таблицу вероятностей попадания случайных величин f в ряд разрядов , считая её распределенной по нормальному закону с параметрами
где Ф – табулированная функция Лапласа , см. таблицу 3. Свойства этой функции: Ф(0) = 0,5Ф(-х) = - Ф(-х),Ф(∞) = 0,5Ф(- ∞) = - 0,5. * 7. Подсчитаем критерий Пирсона по (5.1), имея ввиду, что Рі определяется по выражению (5.4) для каждого разряда (диапазона) , а отвечает числу замеров в опытах для каждого разряда . 8. Определяем число степеней свободы . оно равно разности числа разрядов и числа независимых условий . Такими условиями могут быть: 8.1. Сумма всех частот должна быть равна единице (условие накладывается всегда); Таблица 1
8.2. Совпадение статистического среднего с гипотетическим (предполагаемым); Таблица 2
8.3. Совпадение дисперсий статистического и гипотетического распределений и т.п. Как видно, (см. п.5) в рассмотренном случае соблюдаются также и два последних условия. Таким образом, число степеней свободы определяется по формуле: R = k – d = k – 3 ( 5.5 ) 9. По таблицам 3,4,5,[3] критерий Пирсона х2является распределением для полученных степеней свободы r и по которому для подсчитанного значения х2и определяется уровень значимости Р. Таким образом, если соблюдаются сформулированные высше условия достоверности высказанной гипотезы по уровню значимости Р, то можно сделать вывод о том, что эта гипотеза не противоречит экспериментальным статистически обработанным значениям fi. В частном случае обработки данных по коэффициентам трения fi, это означает, что среднее значение погрешности (среднеквадратичное отклонение) может быть принято в качестве оценки погрешности измерений, а математическое ожидание Результаты обработки:
Приложение 1 Значение функции Лапласа Таблица 3
Значение функции Лапласа Ф(х) для х ≥ 3,0. Таблица 4
*
Приложение 2 Значения х2 в зависимости от r и Р
В ы в о д:
1. В результате статистической обработки экспериментальных данных по коэффициенту трения fиз лабораторной работы №1 можно сделать вывод о том, что экспериментальное значение коэффициента трения fэ = 2. При этом рассчитанная погрешность (отклонение) значения коэффициента fэ, полученного экспериментально, от его теоретического значения fT не превышает допустимой. Литература: 1.Венцель Е.С., Овчаров Л.А. Теория вероятности и ее инженерные приложения. - М.: Наука, гл. ред. физ. мат. лит. - 1988г. (Физико-математическая библиотека инженера) - 480с. 2. Шенк X. Теория инженерного эксперимента. - М.: Мир - 1982г. - 381с. 3. Давыдов В.В. Технические вычисления в кораблестроении. Москва. Морской транспорт. 1991г.-250с. 4. Лабораторная работа №1. Общесудовые устройства и системы. Швартовное устройство. Экспериментальная оценка формулы Эйлера. Кафедра морских технологий НУК им. адмирала Макарова. Николаев 2007 г. (перечень экспериментальных замеров fі, таблицы 1,2,3). Работу выполнил(а): Студент(ка) группы_________ «___»________ 200 г. Фамилия, имя, отчество
Разработка: Зинкин В.Н. Компьютерная верстка: Криницкий Д.А., Стоян В.А.
* Примечание к п. 5. Перед составлением таблицы 2 определить по таблице 1 выборки значений fi разряды (диапазоны) gi ÷ βi количество разрядов k. * Примечание: обозначение в таблице 3, 4: или ;
Поиск по сайту: |
 ;
; ;
;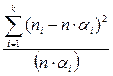 ( 5.1)
( 5.1) можно с большей вероятностью (достоверностью) и достаточной точностью (степенью погрешности эксперимента, принять в качестве точного (среднестатистического) значения величины x. (т. е. xi ≈ xcp=
можно с большей вероятностью (достоверностью) и достаточной точностью (степенью погрешности эксперимента, принять в качестве точного (среднестатистического) значения величины x. (т. е. xi ≈ xcp=  =хточное).
=хточное). ( 5.2 )
( 5.2 ) ( 5.3 )
( 5.3 ) ,
,  . Вероятность Р попадания нормально распределенной величины f на участок от до по формуле
. Вероятность Р попадания нормально распределенной величины f на участок от до по формуле ( 5.4 )
( 5.4 )









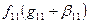




 .
.







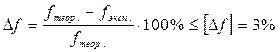

 , для х = 0 ÷ 2,99
, для х = 0 ÷ 2,99 p
r
p
r
 получено с достаточной степенью точности Sf и входит в доверительный интервал его значений fH<
получено с достаточной степенью точности Sf и входит в доверительный интервал его значений fH< ОБЩЕСУДОВЫЕ УСТРОЙСТВА И СИСТЕМЫ
Лабораторная работа № 5
ОЦЕНКА
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
С ПОМОЩЬЮ КРИТЕРИЯ
ПИРСОНА
ОБЩЕСУДОВЫЕ УСТРОЙСТВА И СИСТЕМЫ
Лабораторная работа № 5
ОЦЕНКА
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
С ПОМОЩЬЮ КРИТЕРИЯ
ПИРСОНА