|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
функции представленной разложением в ряд Тейлора»
Цель работы: приобрести практические навыки исследования поведения функции, представленной разложением в ряд Тейлора. Необходимое оборудование и программное обеспечение: для выполнения лабораторной работы необходима ПЭВМ на базе микропроцессора с системой команд ix86, среда программирования любого языка высокого уровня или пакеты математических инструментальных сред, табличный процессор Excel. Задание: Получите у преподавателя № варианта. Выполните разложения функции Вашего варианта в двух точках интервала изменения аргумента в ряд Тейлора (Маклорена), удерживая пять ненулевых членов. Точки разложения выбрать в середине интервала изменения аргумента и на одном из его концах. Для каждой точки разложения получите отдельно три рабочих реализации Вашей функции: первая содержит три ненулевых члена ряда Тейлора, вторая – четыре, третья – пять. Итого должно быть шесть рабочих реализаций. Выполните вычисления и постройте графики: эталонной функции, всех рабочих реализаций, ошибок каждой реализации. Всего должно быть тринадцать графиков. Для каждой реализации рассчитайте среднеквадратичное значение ошибки, математическое ожидание, максимальную приведенную относительную погрешность на всем интервале изменения аргумента. Проанализируйте качество воспроизведение заданной Вам функции. Из всех шести рабочих реализаций выберете одну, которая позволяет вычислять Вашу функцию с приведенной относительной погрешностью 0,5% на наибольшем интервале изменения аргумента. С этой, самой лучшей реализацией, Вы будете выполнять последующие лабораторные работы. Оформите отчет. Содержание отчета: тема, цель работы, используемое оборудование и программное обеспечение, дата проведения эксперимента, № варианта; расчеты коэффициентов рабочих реализаций; графики: эталонной, рабочих реализаций (шесть графиков), ошибок (шесть графиков); числовые характеристики ошибок; анализ и оценка качества воспроизведения заданной функции; выводы. Продолжительность работы. Работа должна быть выполнена за 4 академических часа. Варианты заданий приведены в таблице 1.1 Таблица 1.1
Продолжение таблицы 1.1
32 - Жуков 35 – Сиркина 39 – Сиркин
Пример выполнения лабораторной работы. Исходная функция Получим с помощью Excel значения заданной функции (таблица 1.2) и построим ее график (рисунок 1.1). Эти значения функции и ее график примем как эталонные. Таблица 1.2 Значения заданной функции
Продолжение таблицы 1.2
Рис 1.1. График эталонной функции
Разложение заданной функции в ряд Тейлора в общем виде записывается следующим выражением:
Здесь Если в нашем примере выбрать Учитывая сказанное, выберем Подставляя значения выбранных точек в уравнение (1) и произведя необходимые действия, получим искомые разложения: для
для
Разложения функции в ряды Тейлора с четырьмя и тремя ненулевыми членами можно получить из (2) и (3) путем отбрасывания последних одного или двух членов соответственно. Разложение с тремя ненулевыми членами для
с четырьмя ненулевыми членами для
Разложения для три ненулевых члена
четыре ненулевых члена
Выражения (2), …, (7) являются рабочими. Для обеспечения максимальной точности при реализации рабочих выражений будем подставлять число Результаты расчетов отражают следующие графики для график разложения – рисунок 1.2, график ошибки в пределах 0,5 процента – рисунок 1.3, график ошибки – рисунок 1.4
Рис. 1.3.Ошибка разложения в пределах 0,5%: три члена ряда,
Рис. 1.4.Ошибка разложения: три члена ряда,
Результаты расчетов по рабочей формуле (5) с четырьмя ненулевыми членами для график рабочей реализации – рисунок 1.5; график ошибки – рисунок 1.6; график ошибки в пределах 0,05 процента – на рисунке 1.7.
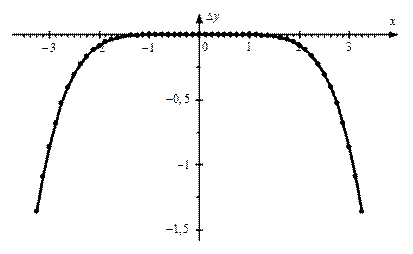
Рис. 1.5.График разложения
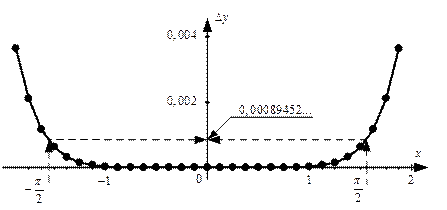
Рис. 1.6.Ошибка разложения: четыре члена ряда,
Рис. 1.7.Ошибка разложения в пределах 0,5%: четыре члена ряда,
На рисунках 1.8, 1.9, 1.10 приведены результаты расчетов по формуле 2 при пяти ненулевых членах ряда и график рабочей реализации – рисунок 1.8; график ошибки – рисунок 1.9; график ошибки в пределах 0,05 процента – рисунок 1.10;
Рис. 1.8.График разложения: пять членов ряда,
Рис. 1.9.Ошибка разложения: пять членов ряда,
Рис. 1.10.Ошибка разложения в пределах 0,5%: пять членов ряда, Результаты расчетов по разложению функции
Рис. 1.11.График разложения пять членов ряда
Рис. 1.12.Ошибка разложения
Как видно из последних двух рисунков, разложение заданной функции В таблице 1.3 приведены статистические числовые характеристики ошибок разложения функции Таблица 1.3 Статистические числовые характеристики ошибок
Проанализируем полученные результаты. Для поставленной задачи, когда необходимо вычислять На основе свойств функции В нашем примере, как следует из рисунка 3, разложение косинуса в ряд Маклорена с тремя членами целесообразно применять для диапазона изменения аргумента Рисунки 1.6 и 1.7 показывают, что четыре члена ряда Маклорена позволяют успешно решать нашу задачу в диапазоне изменения аргумента Пять членов ряда Маклорена дают возможность вычислять косинус угла с приведенной относительной погрешностью в
Рис. 1.13.Ошибка разложения для
Анализируя тенденцию повышения точности вычисления функции Проведенный анализ полученных результатов позволяет сделать выбор рабочей формулы для вычисления функции Задача, поставленная в примере, решена.
Вопросы для самоконтроля.
1. Необходимые условия разложения функции в ряд Тейлора. 2. Отличие ряда Тейлора от ряда Маклорена. 3. Чем определяется сходимость ряда Тейлора. 4. Как определить требуемое число членов ряда Тейлора при разложении заданной функции. 5. Как влияет точка разложения на качество разложения функции в ряд Тейлора. 6. Особенности разложения рядом Тейлора функции, заданной Вам в этой лабораторной работе.
Литература Е.А. Власов Ряды: Учебник для вузов /Под редакцией В.С. Зарубина, А.П. Крищенко.- 3-е изд., исправл.-М.: Изд-во МГТу им. Н.Э. Баумана, 2006.-616с.(Сер. Математика в техническом университете; выпуск IX)
Поиск по сайту: |
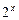
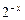
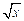
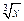
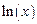
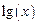
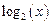
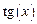
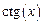

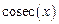

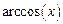
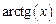
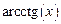
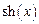
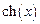

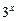
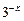
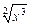
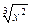
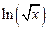

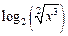
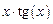
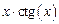

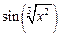

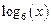
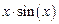

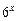
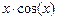
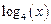
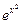
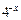
 , диапазон изменения аргумента
, диапазон изменения аргумента 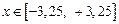 , шаг изменения аргумента
, шаг изменения аргумента 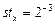 .
.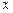
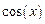
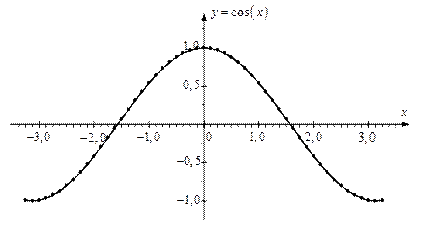
 (1)
(1) точка разложения. Критериями выбора точки
точка разложения. Критериями выбора точки 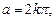
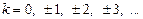 , то вид разложения будет довольно простым. Однако, в виду особенностей функции
, то вид разложения будет довольно простым. Однако, в виду особенностей функции 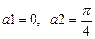 .
.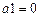 (ряд Маклорена)
(ряд Маклорена)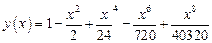 ; (2)
; (2)
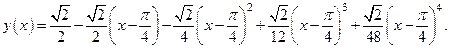 (3)
(3) , (4)
, (4)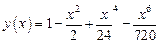 (5)
(5)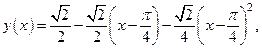 (6)
(6)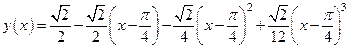 . (7)
. (7)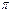 с точностью представления его в выбранном математическом пакете. С этой же точки зрения будем выполнять операции деления непосредственно на 12, 24, 720 и другие целые числа, а не заменять эти операции умножением на коэффициенты в виде округленных периодических дробей. Квадратный корень из двойки также предоставим вычислять математическому пакету.
с точностью представления его в выбранном математическом пакете. С этой же точки зрения будем выполнять операции деления непосредственно на 12, 24, 720 и другие целые числа, а не заменять эти операции умножением на коэффициенты в виде округленных периодических дробей. Квадратный корень из двойки также предоставим вычислять математическому пакету.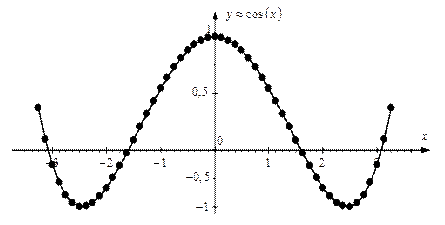 Рис 1.2. График разложения
Рис 1.2. График разложения 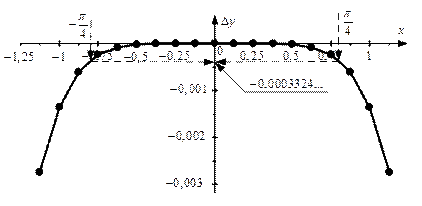

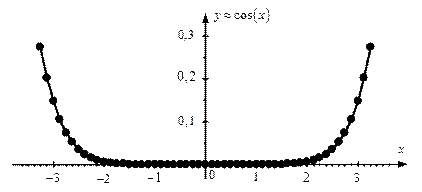
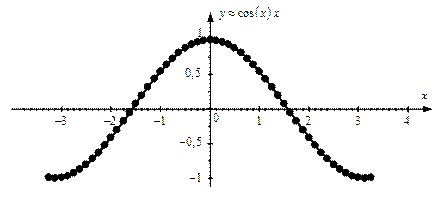
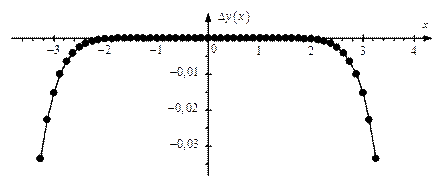
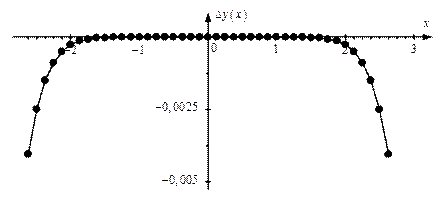
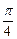 с сохранением пяти членов ряда (рабочая формула (3)) приведены на рисунках 1.11 и 1.12. Рисунок 1.12 – график рабочей реализации, рисунок 1.13 – график ошибки.
с сохранением пяти членов ряда (рабочая формула (3)) приведены на рисунках 1.11 и 1.12. Рисунок 1.12 – график рабочей реализации, рисунок 1.13 – график ошибки.
 ,
,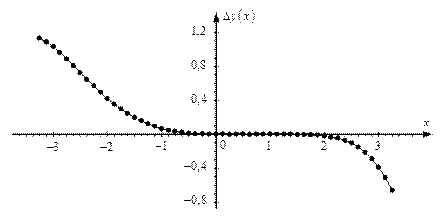
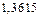

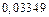
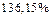

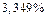


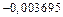
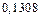

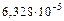
 – не целесообразно. Даже пять членов ряда не позволяют говорить о разработке приемлемого метода решения данной задачи. Эту задачу можно решать лишь используя ряд Маклорена!
– не целесообразно. Даже пять членов ряда не позволяют говорить о разработке приемлемого метода решения данной задачи. Эту задачу можно решать лишь используя ряд Маклорена! ,
, 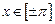 ,
, 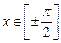 ,
, 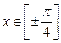 . При этом маленькие диапазоны изменения аргумента требуют больших вычислительных затрат на приведение произвольного аргумента к одному из указанных диапазонов.
. При этом маленькие диапазоны изменения аргумента требуют больших вычислительных затрат на приведение произвольного аргумента к одному из указанных диапазонов. , то необходимо ввести дополнительные вычисления по приведению исходного угла к диапазону
, то необходимо ввести дополнительные вычисления по приведению исходного угла к диапазону 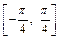 и программу вычисления синуса в этом диапазоне. Логика запоминания истинного октанта расположения аргумента, его знака, логика определения типа рабочей программы, необходимой для применения в конкретном случае (синуса или косинуса), потребуют дополнительных вычислительных ресурсов. При этом считаем, что программа вычисления косинуса угла
и программу вычисления синуса в этом диапазоне. Логика запоминания истинного октанта расположения аргумента, его знака, логика определения типа рабочей программы, необходимой для применения в конкретном случае (синуса или косинуса), потребуют дополнительных вычислительных ресурсов. При этом считаем, что программа вычисления косинуса угла 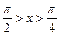 по программе вычисления синуса угла равного
по программе вычисления синуса угла равного 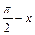 по вычислительной сложности не превосходит программу вычисления косинуса угла в пределах
по вычислительной сложности не превосходит программу вычисления косинуса угла в пределах  .
. в диапазоне изменения этого угла в пределах
в диапазоне изменения этого угла в пределах 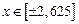 радиан (рисунки 1.9 и 1.10). В этом случае необходимо разработать специальный алгоритм приведения произвольного угла к такому диапазону. Если применять пять членов ряда Маклорена для диапазона изменения аргумента
радиан (рисунки 1.9 и 1.10). В этом случае необходимо разработать специальный алгоритм приведения произвольного угла к такому диапазону. Если применять пять членов ряда Маклорена для диапазона изменения аргумента 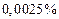 (рисунок 1.13).
(рисунок 1.13).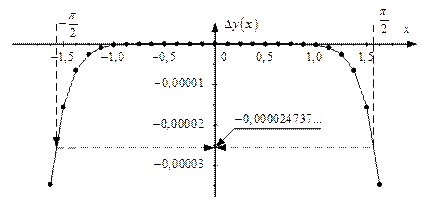
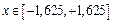 : пять членов ряда,
: пять членов ряда, 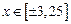 , поставленная задача будет решаться при шести членах ряда, что по условиям нашего примера не допустимо.
, поставленная задача будет решаться при шести членах ряда, что по условиям нашего примера не допустимо. . Этот диапазон очень хорошо вписывается в алгоритм приведения произвольного угла к диапазону
. Этот диапазон очень хорошо вписывается в алгоритм приведения произвольного угла к диапазону