 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
УСТРОЙСТВО СПЕКТРОСКОПА
Муромский институт (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Владимирский государственный университет Имени Александра Григорьевича и Николая Григорьевича Столетовых»
Кафедра: «ФПМ» Дисциплина: физика
Лабораторная работа № 1.01
«Изучение спектра водорода и определение постоянной Ридберга»
Утверждена на методическом семинаре кафедры ФПМ
Зав. кафедрой_____________
ТЕХНИКА БЕЗОПАСНОСТИ
1. Сборку и разборку схемы производить только при отключенном источнике питания. 2. Не включать собранную схему, пока не изучите инструкцию по данной работе и не получите на это разрешение лаборанта или преподавателя. 3. Схема должна находиться под напряжением только во время регулировки и снятия показаний с приборов. КАТЕГОРИЧЕСКИ ЗАПРЕЩАЕТСЯ оставлять схему под напряжением без присмотра. 4. Строго соблюдать порядок выполнения работы, описаний и инструкции. 5. На рабочем месте не должно быть посторонних предметов. Твёрдо знать, где расположен общий выключатель и порядок пользования им. 6. После окончания работы отключить источник питания, а затем разобрать схему и привести в порядок рабочее место. Лабораторная работа № 1.01
«Изучение спектра водорода и определение Постоянной Ридберга»
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: - двухтрубный спектроскоп; - дуговая ртутная лампа; - газоразрядная трубка с водородом, укреплённая в специальном держателе; - выпрямитель.
ВВЕДЕНИЕ
1.1 Закономерности в атомных спектрах
Разряженные газы, пары металлов испускают спектр, состоящий из отдельных спектральных линий. В соответствие с этим спектр испускания веществ, образованный возбужденными атомами называется линейчатым спектром. Изучение атомных спектров послужило ключом к познанию строения атомов. Прежде всего, было замечено, что линии в спектрах многих атомов расположены не беспорядочно, а объединяются в группы, или как их называют серии спектральных линий. Отчётливее всего это обнаруживается в спектре простейшего атома – водорода. Швейцарский физик Бальмер в 1885 году установил, что длины волн спектральных линий в видимой области спектра укладываются в простейшую формулу:
где В спектроскопии принято характеризовать спектральные линии величиной, обратной длине волны Если преобразовать формулу (1) в выражение для чисел, то получим:
где
R=10973730,9 Дальнейшие исследования показали, что в спектре водорода имеется ещё несколько серий. Оказывается, что волновые числа всех серий в спектре атомарного водорода можно выразить одной формулой, обобщающей формулу Бальмера (2):
Из (3) находим волновые числа всех линий. 1. Серия Лаймана. Находится в ультрафиолетовой области спектра. Для неё
2. Серия Бальмера. Находится в видимой области спектра. Для неё
3. Серия Пашена. Находим в ближайшей инфракрасной области. Для неё
В инфракрасной области обнаружено ещё несколько серий.
1.2 Атом водорода по теории Бора. Опытами Резерфорда по рассеянию Выход из создавшегося (положения) тупика был найден в 1913 году датским физиком Бором на основании предположений, противоречащих классической физике. Эти предположения содержатся в двух высказанных им постулатах. 1) Из бесконечного множества электронных орбит, возможных с точки зрения классической физики, осуществляются только определенные, стационарные орбиты, для которых орбитальный момент количества движения (импульс)
или  , , 
где  , а , а  1, 2, 3,…. 1, 2, 3,….
Пока электрон движется по стационарной орбите, атом не излучает и не поглощает света. 2) При переходе электрона с одной стационарной орбиты на другую происходит излучение или поглощение кванта света, энергия которого равна разности энергий электрона при движении по соответствующим стационарным орбитам с номерами
Если Рассмотрим атом водорода и предположим, что электрон вокруг ядра движется по круговым орбитам. Используя формулу (4) и применяя закон Ньютона к движению электрона:
Найдём радиус электронных орбит:
и скорости электронов на них:
Легко найти и энергию атома водорода при движении электрона по стационарной орбите.
Исходя из условия частот Бора (5) и вводя в рассмотрение волновое число, получим:
Сравнивая с (3), получим, что
В (8) запишется:
Числа
1.3. Квантовомеханическая теория атома водорода. Теория Бора объяснила все основные закономерности в спектре водорода. Однако она не смогла построить теорию атома гелия. Самой слабой стороной теории Бора была ее внутренняя противоречивость. Эта теория не была ни последовательно классической, ни последовательно квантовой. Она представляет собой лишь переходный этап на пути к созданию последовательной теории атомных явлений. Такой теорией стала квантовая механика. В 1924 году французский физик Луи де Бройль выдвинул гипотезу о том, что все микрочастицы обладают волновыми свойствами. По идее де Бройля с движением микрочастиц связана волна. Эти волны имеют длину
Состояние движения микрочастиц описывается волновой функцией координат частицы и времени
а Физический смысл волновой функции состоит в том, что квадрат ее модуля дает плотность вероятности (вероятность, отнесенную к единице объема) нахождения частицы в соответствующем объеме пространства.
Волновая функция может быть найдена путем решения уравнения:
 (11). (11).
Это уравнение получено Шредингером в 1926 году и называется временным уравнением Шредингера. Здесь Как видно из (2) вид волновой функции определяется потенциальной энергией
 (12). (12).
Здесь Е - полная энергия частицы, U - ее потенциальная энергия. Решение уравнения (12) позволяет найти волновые функции и полную энергию любой квантовомеханической системы. Применим уравнение Шредингера для атома водорода. В атоме водорода потенциальная энергия равна:
где r – расстояние электрона от ядра. Потенциальное поле обладает сферической симметрией. Удобно внести в рассмотрение сферические координаты
 (13). (13).
Это уравнение имеет физически обоснованные решения при любых положительных значениях энергии Е и при дискретных отрицательных значениях Е равных:
 , где n = 1,2,3,…. (14) , где n = 1,2,3,…. (14)
Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся в бесконечность. Случай Е < 0 соответствует электрону, находящемуся в пределах атома. Сравнивая (14) и (7) видно, что квантовая механика приводит к тем же значениям энергии атома водорода, что и теория Бора. Однако в квантовой механике эти значения получаются логическим путем из ее основных положений без каких-либо дополнительных предположений. Число n, определяющее значение энергии электрона в (14) называется главным квантовым числом. Решение уравнения (13) дает значения орбитального момента импульса (количества движения) электрона. LZ = где Из решения уравнения (13) следует, что ряд дискретных значений принимает так же проекция орбитального момента на выделенное направление в пространстве (оно обычно принимается за направление оси OZ - направление магнитной индукции).
где
Каждому значению энергии Е соответствует несколько состояний электрона в атоме, отличающихся значением квантовых чисел
Состояние с Е=0 соответствует поляризованному атому водорода. Рассмотрим основное состояние атома водорода (n=1). Для него
Рисунок 1
УСТРОЙСТВО СПЕКТРОСКОПА Для исследования видимой части спектра служат различные спектроскопы. Один из наиболее простейших изображен на рис.2. Двухтрубный спектроскоп состоит из коллиматора "К", столика с призмой "П" и зрительной трубы "З", которая перемещается относительно призмы микрометрическим винтом "В". Длина трубки коллиматора (расстояние между щелью и линзой) такова, что щель, являющаяся вторичным источником света, находится в фокальной плоскости линзы. Поэтому после линзы лучи к призме идут параллельным пучком. Пройдя через призму, лучи будут отклоняться по-разному, в зависимости от их длины волны. Так как лучи с одной и той же длиной волны после призмы также параллельны между собой, то они собираются в одной точке (точнее, на линии, представляющей собой изображение щели коллиматора, проходящей через одну из точек фокальной плоскости объектива зрительной трубы). Для получения необходимого увеличения, полученные спектральные линии рассматриваются с помощью окуляра с нитью для отсчета. Чтобы перейти от одной линии спектра к другой, перемешают миллиметровые деления, а барабан винта разделен на 50 частей. Ход винта равен 1мм, следовательно, цена деления на барабане винта:
Положения каждого изображения щели можно характеризовать отсчетом на винте и барабане. Выполняемая работа состоит из 2-х частей.
ВЫПОЛНЕНИЕ РАБОТЫ Упражнение 1. Градуировка спектроскопа. Градуирование спектроскопа производится с целью выразить показания микрометрического винта в длинах волны. Для этой цели используют источник света с хорошо изученным спектром. В качестве такого источника в данной работе используется дуговая ртутная лампа, помещенная в специальный кожух, укрепленный на подставке. Можно для градуировки спектроскопа воспользоваться газоразрядной трубкой, наполненной гелием. Градуирование спектроскопа производится следующим образом: 1. Устанавливают коллиматор спектроскопа на расстояние 10-15 см от щели кожуха ртутной лампы. Включают лампу в сеть. Через 2-3 мин. лампа ярко разгорается. Перемещением спектроскопа добиваются появления в поле зрения зрительной трубы спектра ртутной лампы. Перемещая окуляр зрительной трубы спектроскопа, получают четкое изображение спектральных линий. 2. С помощью микрометрического винта устанавливают нить окуляра зрительной трубы на крайнюю спектральную линию (красную) в спектре ртутной лампы и записывают показания микрометрического винта. Затем последовательно переводят нить окуляра на все яркие линии, записывая каждый раз показания винта. Затем повторяют измерения, перемещая зрительную трубку в обратном направлении. Результаты измерений заносят в таблицу.
Таблица - Длина волны некоторых линий в спектрах ртутной лампы.
3. Зная длины волн спектральной линии ртутной лампы, строят график градуировки, откладывая по оси ординат длины волн, а по оси абсцисс показания микрометрического винта.
Рисунок 2
Упражнение 2.Изучение спектра водорода. 1. Отключают ртутную лампу. Не перемещая спектроскоп, устанавливают между лампой и спектроскопом, подставку с газоразрядной трубкой, наполненной водородом. Наводят зрительную трубу на наиболее интенсивные линии в спектре водорода и записывают показания микрометрического винта. 2. По графику определяют длины волн спектральных линий водорода и на основании формулы (2) вычисляют постоянную Ридберга. В спектре водорода возможно появление слабых линий, принадлежащих молекулам (Н2). Эти линии, следует пропустить. Обычно для атомарного водорода в видимой части спектра наблюдается 3-4 наиболее интенсивных линий. Результаты измерений оформить в виде таблицы.
Поиск по сайту: |
 (1),
(1), - целое число, принимающее значения 3, 4, 5, 6 и т. д.
- целое число, принимающее значения 3, 4, 5, 6 и т. д.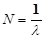 , которая называется волновым числом.
, которая называется волновым числом. (2),
(2),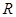 - постоянная Ридберга
- постоянная Ридберга 0,012 см
0,012 см  или
или  107 м
107 м  (3).
(3). =1,
=1,  =2, 3, 4, 5, и т. д.:
=2, 3, 4, 5, и т. д.: .
. .
. -частиц веществом была обоснована ядерная (планетарная) модель атома. Однако ядерная модель атома оказалась в противоречии с законами классической механики и электродинамики. Классическая теория не смогла объяснить ни устойчивости атомов, ни дискретный (линейчатый) спектр атомов.
-частиц веществом была обоснована ядерная (планетарная) модель атома. Однако ядерная модель атома оказалась в противоречии с законами классической механики и электродинамики. Классическая теория не смогла объяснить ни устойчивости атомов, ни дискретный (линейчатый) спектр атомов. (4),
(4),

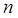 и k
и k (5).
(5). >
>  , то имеет место излучение света. Когда наблюдается
, то имеет место излучение света. Когда наблюдается  (6).
(6).

 (7).
(7). (8).
(8). .
.
 и
и  получили название спектральных термов. Они пропорциональны энергии стационарных состояний атома.
получили название спектральных термов. Они пропорциональны энергии стационарных состояний атома. (9).
(9). . Например, с движением свободной частицы связана плоская волна, уравнение которой может быть записано в виде:
. Например, с движением свободной частицы связана плоская волна, уравнение которой может быть записано в виде: (10), где
(10), где  - соответствующие импульсы частицы;
- соответствующие импульсы частицы; - её энергия.
- её энергия.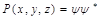
 - комплексное сопряжение с
- комплексное сопряжение с  .
.

 - потенциальная энергия частицы.
- потенциальная энергия частицы. , т.е. природой всех сил, которые действуют на частицу. Для стационарных состояний уравнение Шредингера примет вид:
, т.е. природой всех сил, которые действуют на частицу. Для стационарных состояний уравнение Шредингера примет вид:

 , тогда уравнение Шредингера запишется:
, тогда уравнение Шредингера запишется:
 (15),
(15), - азимутное или орбитальное квантовое число, принимающее значения
- азимутное или орбитальное квантовое число, принимающее значения 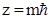 (16),
(16), - магнитное квантовое число, принимающее значения
- магнитное квантовое число, принимающее значения  1,
1,  - значения для данного
- значения для данного 



 n=4
n=4

