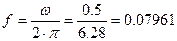|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лабораторная работа №1. По дисциплине: «Компьютерное управление мехатронными системами»
По дисциплине: «Компьютерное управление мехатронными системами» На тему: «Дискретизация и квантование непрерывных сигналов» В-III
Выполнил: ст. гр. МТ-91 Яковлев И.А.
Проверил: к.т.н., ст. преподаватель Яцун А.С.
Курск, 2013 г. Цель работы:исследование влияние частоты дискретизации на точность восстановленных сигналов. Исследование эффекта поглощения частот. Выполнение работы: Заданная функция: y(t)=cos(0.5t)+sin(0.08t) График приведённой функции представлен на рисунке 1:
Рис.1 График зависимости функции y(t)=cos(0.5t)+sin(0.08t) от времени t
Выберем время квантования сигнала T=5 c. Полученные дискретные отсчёты (рисунок 2) соединим прямыми:
Рис.2 Графики зависимостей исходной функции y(t) и функции полученной в результате квантования u от непрерывного времени t и дискретного времени T Применим быстрое преобразование Фурье для получения спектра частот для заданной функции (рисунок 3):
Рис.3 Частотный спектр функции y(t)=cos(0.5t)+sin(0.08t)
Вычислим максимальную частоту. В исходной функции y(t)=cos(0.5t)+sin(0.08t) наибольшую круговую частоту имеет cos(0.5t), то Как видно из результатов, максимальная частота приближённо совпадает с максимальной частотой спектра на рис. 3.
Рис.4 Частотный спектр функции y(t)=cos(0.5t)+sin(0.08t) Согласно теореме Котельникова-Найквиста(Шеннона), частота квантования должна быть в 2 и более раз быть больше найденной т.е. Частота квантования при этом будет равна:
Функция cos(0.5t) находится в максимуме в нулевой момент времени, то квантование начинаем с T.
Рис.5 Графики зависимостей исходной функции y(t) и функции u, полученной в результате квантования с частотой fs от непрерывного времени t и дискретного времени T
Если взять частоту квантования меньше, чем, частота спектра, то мы будем наблюдать так называемый эффект поглощения частот: частота квантования окажется недостаточной для качественной передачи сигнала. При увеличении частоты квантования качество получаемого сигнала значительно увеличивается. Например для частоты квантования f=8fs почулим следующую диаграмму (рисунок 6):
Рис.6 Графики зависимостей исходной функции y(t) и функции u, полученной в результате квантования с частотой 8*fs от непрерывного времени t и дискретного времени T
Выводы: в ходе лабораторной работы была экспериментально проверена и доказана теорема Котельникова-Найквиста(Шеннона0 для квантования сигнала. При частоте квантования меньше, чем fs, непрерывный сигнал квантуется некачественно (возникает эффект «поглощения частот»). При квантовании с частотой больше или равной fs мы получаем качественный дискретный сигнал без потери информации.
Поиск по сайту: |