 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Синтез цифровых систем управления.
При проектировании как цифровых, так и непрерывных систем управления приходится решать, по сути дела, одни и те же задачи. Чаще всего речь идет о процессе, которым нужно управлять таким образом, чтобы его выходные переменные удовлетворяли некоторым заранее установленным критериям качества. Традиционная философия проектирования вначале приводит проектировщика к решению об использовании обратной связи для образования сигнала ошибки между входным и выходным сигналами. Затем выясняется необходимость применения регулятора, который обрабатывал бы сигнал ошибки так, чтобы удовлетворить все требования, предъявляемые к качеству системы. В цифровых системах решение аналогичной задачи отличается большой гибкостью и имеет множество вариантов. Например, при использовании цифровых или дифференциальных датчиков, выходной сигнал которых имеет дискретный характер, система управления объективно является цифровой или дискретной. Возможен также случай, когда проектировщик намеренно включает в состав системы цифровой регулятор. В свою очередь, если цифровой сигнал сглаживается фильтром, то можно использовать и аналоговый регулятор. Таким образом, когда речь идет о проектировании цифровой системы управления, то существует множество структурных решений, и окончательный выбор полностью находится во власти проектировщика. Методы синтеза цифровых систем управления могут быть основаны на описании системы переменными состояниями либо на описании системы с постоянными параметрами. В основе традиционных методов синтеза лежит идея о жестко заданной структуре системы, когда проектировщик с самого начала устанавливает ее конфигурацию, включая управляемый процесс и регулятор. Мощным средством синтеза систем в пространстве состояний является использование обратной связи по переменным состояния или по выходу, причем предполагается, что все эти переменные доступны наблюдению. На практике это условие не всегда выполняется, поэтому необходимо либо использовать наблюдатель, дающий оценку всех или некоторых переменных состояния, либо просто осуществлять обратную связь по выходу. Наиболее универсальным способом организации цифровых систем управления является применение цифрового регулятора. Функцию цифровых регуляторов (контроллеров) могут выполнять в том числе импульсные фильтры и микроЭВМ. По сравнению с аналоговым регулятором, цифровой регулятор в состоянии обеспечить гораздо лучшее качество системы управления. Другое преимущество систем с цифровыми регуляторами заключается том, что алгоритм управления легко может быть изменен сменой программы контроллера, когда контроллер построен на основе микропроцессора. В аналоговых регуляторах сделать это намного труднее. Существует множество практических способов реализации цифрового регулятора. При построении цифрового регулятора на основе микроЭВМ, необходимо помнить, что ЭВМ присущи такие лимитирующие факторы, как разрядность, объем памяти и скорость счета.
Микропроцессор как управляющее устройство систем управления. Рассмотрим некоторые аспекты программирования реальной системы на основе микропроцессорного устройства. Возможный вариант использования микропроцессора (МП) в системе управления двигателем постоянного тока в составе комплектного привода приведен на рис. 1.5.
Рис. 1.8. Структура процессорной системы управления приводом.
Управляемый привод и микропроцессор связаны через аналого-цифровой (АЦП) и цифроаналоговый (ЦАП) преобразователи. Таким образом, вся система рассматриваться как цифровая система управления с периодом квантования Т секунд. Пусть целью управления этой системы с двигателем постоянного тока является поддержание скорости нагрузки w(t) постоянной, равной значению задаваемой скорости wd(t). Тогда ошибка между задаваемой скоростью и скоростью нагрузки определяется как e(t) = wd(t)-w(t) (1.42) На входе микропроцессора имеется дискретный сигнал ошибки e(k∙T), k=0,1,2, ..., n. Сигнал на выходе микропроцессора обозначим u(k∙T). Предположим, что микропроцессор должен совершать цифровые вычисления для реализации пропорционально-интегрального (ПИ) регулятора, описываемого в непрерывной форме как
Интеграл в последнем выражении может быть записан в виде
где t0 - начальный момент времени; х(t0) - начальное значение. Для вычисления интеграла могут быть использованы различные методы. Будем использовать метод трапеций и положим t=k∙T, t0=(k-1)·t. Тогда определенный интеграл в выражении (1.44) запишется как
где t0 – начальный момент времени, x(t0) – начальное значение x(t), k=1,2,…,n. Следовательно, значение интеграла для t=kT может быть вычислено по задаваемой скорости wd и значениям w(kT) и w[(k-1)Т]. Рассчитанное значение управления прикладывается к системе с двигателем постоянного тока при t=(k+1)T, k=0,1,2, … n. Управление изменяется каждые Т секунд и остается постоянным между моментами расчета. Функциональная схема рассмотренной микропроцессорной системы, используемой для реализации цифрового ПИ-регулятора, приведена на рис. 1.6.
Рис. 1.9. Структура функциональных составляющих системы управления.
В этой системе для определения начала следующего периода квантования применен программируемый таймер, который вырабатывает импульс каждый Т секунд. Этот импульс поступает на шину прерываний микропроцессора, что приводит к остановке рабочей программы и выполнению программы прерывания, которая выводит следующее значения управления u[(k + 1)t]. Это управление передается в ЦАП, выходной сигнал которого поступает на вход тиристорного преобразователя. Импульс таймера запускает процесс АЦП-преобразования текущей скорости двигателя w(t) в двоичный код. Для этого процесса требуется конечное время. Следовательно, АЦП должен сообщить микропроцессору через шину готовности о том, что данные преобразованы. После этого процессор вводит значение wd(k·T), и вычисляет следующее значение управления u[(k+1)∙T], которое используется для управления приводом при следующем прерывании от таймера. Аналогично может быть реализован ПИД-регулятор. Приведенный пример показывает, как управление двигателем постоянного тока может быть реализовано на базе микропроцессора. На начальной стадии решения задачи регулятор описывается дифференциальным уравнением. Последнее записывается с применением одного из приближенных численных методов в дискретной форме для моментов выборки, после чего разрабатывается программа для микропроцессора.
Ограничения микропроцессорных систем управления. При использовании микропроцессора проектировщик системы должен принимать во внимание конечную длину слова и временные задержки, возникающие при работе программного обеспечения, а так же нелинейность и другие погрешности АЦП преобразования. В цифровых, микропроцессорных системах управления, вообще говоря, сигналы на входе и выходе являются усеченными. При этом параметры закона управления будут округлены при его реализации в процессоре с помощью рабочей программы. Следовательно, параметры системы могут быть реализованы только конечным набором чисел. На качество микропроцессорных систем управления влияет как конечная длина слова микропроцессора, так и точность выполнения арифметических операций с плавающей точкой.
Поиск по сайту: |


 (1.43)
(1.43)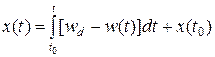 (1.44)
(1.44) (1.45)
(1.45)