 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задача виявлення сигналуСтр 1 из 2Следующая ⇒
Лектор ст. викл. Нагорна Ніна Миколаївна РОЗДІЛ 7 ПРИЙМАННЯ ІНФОРМАЦІЇ
Структура приймального пристрою
Приймальний пристрій містить два основних елементи (рис. 7.1):
- фільтр; - розв’язувальний пристрій (РП).
Рисунок 7.1 – Структурна схема приймального пристрою
На вхід приймального пристрою надходить сигнал Y(t), який є сумою корисного сигналу та сигналу завади. На виході фільтра формується сигнал зі збільшеним відношенням сигнал/шум. Відношення сигнал/шум на виході фільтра – це відношення миттєвого значення корисного сигналу до середньоквадратичного рівня шуму. Розв’язувальний пристрій служить для виявлення, розпізнавання і відновлювання сигналів. В фільтрах використовуються наступні методи фільтрації:
- частотна фільтрація; - метод накопичення; - кореляційний метод; - узгоджена фільтрація.
Частотна фільтрація
При частотній фільтрації завади подавляються. Розглянемо найчастіші випадки.
Випадок 1. На вхід приймача надходить вузькосмуговий сигнал і широкосмугова завада. В цьому разі у тракт приймального пристрою вводиться вузькосмуговий фільтр зі смугою пропускання Випадок 2. На вхід приймача надходить широкосмуговий сигнал і вузькосмугова завада. У цьому разі фільтр повинен подавити заваду в смузі частот
а б
а – спектральні густини вузькосмугового сигналу б - спектральні густини широкосмугового сигналу
Рисунок 7.2 – Спектральні густини сигналу
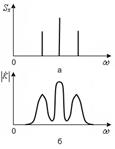
Випадок 3. На вхід приймача надходить періодичний сигнал і широкосмугова завада. Періодичний сигнал має дискретний частотний спектр. У цьому разі в приймальний пристрій включається набір фільтрів, що пропускають лише дискретні частоти періодичного сигналу. Спектр періодичного сигналу і амплітудно-частотна характеристика гребінчастого фільтра показані на рис. 7.3. Недолік частотної фільтрації: підвищення відношення сигнал/шум виконується за рахунок збільшення часу передавання сигналу і його спостерігання.
Рисунок 7.3 – Спектр періодичного сигналу (а) і амплітудно-частотна характеристика гребінчастого фільтра (б) Метод накопичення При використанні методу накопичення сигнал повинен бути або постійним протягом часу приймання, або являтися періодичною функцією. Метод полягає у багатократному повторенні сигналу і підсумовуванні окремих його реалізацій у приймальному пристрої.
Якщо завади адитивні, то за рахунок збільшення числа відліків, тобто часу передавання, можливо скіль завгодно збільшити відношення сигнал/завада. Якщо сигнал є періодичною функцією часу, то інтервали відліків повинні бути кратними періоду функції. У цьому разі метод називається методом синхронного накопичення. При постійному або квазіпостійному сигналі використовують метод інтегрального приймання, в якому вхідний сигнал інтегрується. Завадостійкість інтегрального приймання тим вище, чим більше час інтегрування і чим більш високочастотна завада присутня у сигналі. Кореляційний метод Сутність методу полягає в урахуванні різниці кореляційних функцій сигналу і завади.
Метод використовується лише при прийманні періодичних і квазіперіодичних сигналів. Нехай корисний сигнал є періодичним, а завада типу гаусова шуму. У цьому випадку сигнал і завада статистично незалежні. Тоді можливо записати:
де
З аналізу представлених графіків (рис. 7.4) можна побачити, що при
а
б
в
Рисунок 7.4– Кореляційні функції завади (а), корисного сигналу (б), вхідного сигналу (в) тільки корисний сигнал. Величина
Приклад 1. Нехай сигнал y має прямокутну форму (рис. 7.5, а). Рисунок 7.5 –Залежності сигналів y(t), y(t-t) від часу (а) і функція автокореляції сигналу y (б)
На підставі того, що функція автокореляції сигналу y
добуток Тоді функція автокореляції сигналу y розраховується за формулою:
Кореляційний приймач містить наступні блоки (рис. 7.6):
- блок затримки; - блок множення; - інтегратор.
Рисунок 7.6 – Структурна схема кореляційного приймача
Вибір часу приймання сигналу
При збільшенні
Узгоджена фільтрація Узгоджені (оптимальні) фільтри служать для виділення корисного сигналу відомої форми на фоні шумів. Наприклад, узгоджену фільтрацію можливо використовувати при прийманні радіолокаційного сигналу, бо у цьому разі корисний сигнал є точною масштабною копією сигналу, що передається. Узгоджені фільтри максимізують відношення сигнал/шум в деякий момент часу t0. Частотний коефіцієнт передачі узгодженого фільтра повністю визначається спектральною густиною корисного сигналу. Нехай корисний сигнал (прямокутний відеоімпульс) на вході узгодженого фільтра і його функція автокореляції мають вид, показаний на рис. 7.7, а, б.
а б в
а – прямокутний відеоімпульс; б – функція автокореляції прямокутного імпульсу; в – сигнал на виході фільтра
Рисунок 7.7 – Ілюстрація до принципу роботи узгодженого фільтра
Сигнал на виході фільтра, що узгоджений з прямокутним відео-імпульсом, для випадку, коли
де В – постійний коефіцієнт.
Особливість узгодженої фільтрації: чим вище енергія корисного сигналу, тим імовірність його виявлення вища. Завжди можливо добитися надійного виявлення сигналу дуже малої амплітуди, якщо збільшити тривалість імпульсу. Але при цьому буде зменшуватися швидкість передавання інформації по каналу.
Задача виявлення сигналу Задача виявлення сигналу розв’язується на основі положень теорії статистичних рішень. При її розв’язанні встановлюється, чи є у прийнятому сигналі корисний сигнал. Нехай прийнятий сигнал
де
Нехай корисний сигнал може приймати 2 значення:
Тоді
Розв’язувальний пристрій повинен з’ясувати, яка з гіпотез правильна (вірна): - гіпотеза H1 – корисний сигнал є у прийнятому сигналі; - гіпотеза H2 – корисний сигнал відсутній.
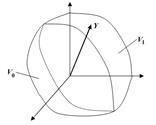
Геометрична інтерпретація задачі показана на рис. 7.8.
Рисунок 7.8 – Геометрична інтерпретація задачі виявлення сигналу
Простір прийнятих сигналів V умовно розбивається на 2 частини: - область V1, що відповідає прийняттю гіпотези Н1 про те, що х=х1; - область V0 , що відповідає прийняттю гіпотези Н0 про те, що х=х0. Якщо вектор прийнятого сигналу Y виявиться в області V0, то приймається гіпотеза Н0, якщо в V1 – то Н1. В цих умовах можуть мати місце два значення апостеріорної ймовірності P(X, Y), а саме: P(X0/Y) – умовна ймовірність відсутності корисного сигналу при прийнятті сигналу Y (при даному значенні вибірки Y); P(X1/Y) – умовна ймовірність наявності корисного сигналу (при даному значенні вибірки Y); X, Y – вектори.
Для визначення апостеріорних імовірностей P(X,Y) або густин імовірностей w(X/Y) необхідно знати умовну густину ймовірності Y, якщо заданий Х, тобто w(Y/Х), яка при заданому значенні Y буде залежати тільки від Х: w(Y/Х)=L(X),
де L(X) – функція правдоподібності.
Апостеріорна густина ймовірності w(X/Y) розраховується по формулі Байєса
де w(X) – апріорна густина ймовірностей вектора Х; w(Y) – безумовна густина ймовірностей вектора Y; w(Y /Х) – умовна густина ймовірностей вектора Y, якщо заданий вектор Х. В задачі виявлення розглядаються два значення функції правдоподібності:
L(x1)=w(Y/x1) – умовна густина ймовірностей вибірки Y при наявності корисного сигналу х1. L(x0)=w(Y/x0) - умовна густина ймовірностей вибірки Y при відсутності корисного сигналу. Відношенням правдоподібності називається відношення функцій правдоподібності:
Для вибору гіпотези Н1 або Н0береться за основу деяке вирішувальне правило (синоніми: вирішувальна функція, стратегія, алгоритм розпізнавання). Для вибору вирішувального правила використовують такі критерії:
- максимума правдоподібності; - максимума апостеріорної ймовірності; - ідеального спостерігача (критерій Котельникова); - Неймана-Пірсона; - мінімального ризику (критерій Байєса); - мінімаксний критерій.
Правила прийняття рішень, що відповідають переліченим критеріям, мають однакову форму запису:
Відмінність проявляється лише у величині Значення
Таблиця 7.1 – Порогове значення відношення правдоподібності для окремих критеріїв
Поиск по сайту: |

 (рис 7.2, а).
(рис 7.2, а). (рис 7.2, б).
(рис 7.2, б).
 і широкосмугової завади
і широкосмугової завади  ;
;
 ,
, - часовий зсув;
- часовий зсув;  - автокореляційна функція вхідного сигналу;
- автокореляційна функція вхідного сигналу; ,
,  - автокореляційні функції корисного сигналу і завади.
- автокореляційні функції корисного сигналу і завади. значенням
значенням  можливо знехтувати. При цьому
можливо знехтувати. При цьому  буде містити
буде містити
 .
.
 ,
, відрізняється від нуля на інтервалі від
відрізняється від нуля на інтервалі від  , де
, де  .
.
 і від відношення сигнал/завада.
і від відношення сигнал/завада. зростає інтервал
зростає інтервал  можливо знехтувати. Час кореляційного приймання практично визначається нерівністю:
можливо знехтувати. Час кореляційного приймання практично визначається нерівністю: 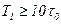 .
.
 має вид (рис. 7.7, в):
має вид (рис. 7.7, в): ,
, ,
, - корисний сигнал,
- корисний сигнал,  - завада.
- завада. - сигнал є;
- сигнал є;  - сигналу немає.
- сигналу немає. .
.
 ,
,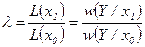 .
.
 .
.

 знаходиться з умови
знаходиться з умови 

 , де
, де  і
і  знаходяться з умови
знаходяться з умови  .
.