 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Решение матричной игры в чистых стратегиях
Математиком А. Вальдом был сформулирован принцип суть которого состоит в том, что при принятии решения в условиях неопределенности разумно исходить из того, что сложится наименее благоприятная ситуация. Исходя из этого принципа игрок 1 может рассуждать следующим образом: «Предположим, что я выберу
где Определение.Число Аналогично, второй игрок, также исходя из наихудшего исхода, должен рассуждать следующим образом: «Предположим, что я выберу
Тогда я должен выбрать такой столбец, т.е. ОпределениеЧисло ТеоремаНижняя цена игры не превосходит верхней цены игры. Если для некоторой игры верхняя и нижняя цены равны, т.е. выполняется
где
Сравнивая это неравенство с (3) видим, что оказывается ситуация ОпределениеИгра, для которой Пример 2Для игровой матрицы из примера 4.1 найти седловые точки, если они есть. Нахождение нижней и верхней цен игры, равно как и проверка существования седловых точек и их нахождение, для матричных игр удобно проводить по следующей схеме
Видно, что максимин имеет место в 1-й строке, т.е. при первой стратегии 1-го игрока. Минимакс - в первом столбце, т.е. при 1-й стратегии 2-го игрока. При этом они совпадают, т.е. имеется седловая точка. Это ситуация
Поиск по сайту: |
 -ю стратегию, тогда в худшем для меня случае я получу выигрыш величиной
-ю стратегию, тогда в худшем для меня случае я получу выигрыш величиной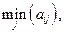

 -количество строк в матрице игры, т.е. количество чистых стратегий 2-го игрока. Тогда я должен выбрать такую строку, т.е.
-количество строк в матрице игры, т.е. количество чистых стратегий 2-го игрока. Тогда я должен выбрать такую строку, т.е. 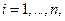
 - количество столбцов в матрице игры), при которой этот минимум максимальный».
- количество столбцов в матрице игры), при которой этот минимум максимальный». называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) - максиминной.
называется нижней ценой игры или максимином, а соответствующая ему стратегия (строка) - максиминной.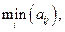

 -ю стратегию, при которой этот максимум минимальный»
-ю стратегию, при которой этот максимум минимальный» называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) - минимаксной.
называется верхней ценой игры или минимаксом, а соответствующая ему стратегия игрока (столбец) - минимаксной. , или что то же самое
, или что то же самое
 - соответствующий элемент матрицы игры, то очевидно для этого элемента выполняется неравенство
- соответствующий элемент матрицы игры, то очевидно для этого элемента выполняется неравенство
 является равновесной, т.е. оптимальной, т.е. решением игры. Величина
является равновесной, т.е. оптимальной, т.е. решением игры. Величина  при этом, очевидно, является ценой игры, т.е. рассматриваемые принципы максимина и минимакса приводят к оптимальному и равновесному состоянию. Это еще раз свидетельствует об обоснованности их использования при принятии решений.
при этом, очевидно, является ценой игры, т.е. рассматриваемые принципы максимина и минимакса приводят к оптимальному и равновесному состоянию. Это еще раз свидетельствует об обоснованности их использования при принятии решений. называется игрой с седловой точкой.
называется игрой с седловой точкой.
