 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Описание общей модели Вальраса
Рассмотрим математическое моделирование рынка по Вальрасу. Исходными концепциями модели Вальраса являются: · дезагрегированность участников рынка: рассматриваются отдельные потребители и отдельные производители; · совершенность конкуренции; · общность равновесия. Последняя концепция означает рассмотрение равновесия по всем товарам сразу, а не по отдельным товарам. Следовательно, в модели Вальраса вводится понятие общего равновесия (т.е. равновесия по всем товарам). Будем предполагать, что на рынке продаются и покупаются товары двух видов: готовые товары, являющиеся продуктом производства (товары конечного потребления) и производственные ресурсы (первичные факторы производства). Поэтому будем рассматривать «расширенное» пространство товаров Индексы (виды) товаров, как и раньше, будем обозначать буквой Выходя на рынок, каждый потребитель или производитель становится одновременно покупателем одних и продавцом других товаров. Потребитель, т.е. участник рынка, «непосредственно не занятый в производстве», может продавать имеющиеся в его распоряжении первичные факторы и покупает товары производителей. Производитель, т.е. участник рынка, «непосредственно занятый в производстве», продает свою готовую продукцию и покупает первичные факторы у потребителей. Поэтому каждый потребитель i как участник рынка характеризуется тремя параметрами: начальным запасом товаров Каждый производитель j характеризуется двумя параметрами: вектор-функцией предложения готовой продукции Следовательно, под математической моделью рынка понимают совокупность элементов:
где Без качественных потерь вместо (4.3.1), как модель рынка, можно рассматривать совокупность
Природа элементов совокупности (4.3.1) здесь несколько отличается от той, которая характеризовалась при изолированном рассмотрении потребительского и производственного секторов. Во-первых, вектор Исходя из технических соображений, будем предполагать, что пространство цен P включает в себя нуль пространства Во-вторых, как уже говорилось выше, каждый участник рынка выступает в двух лицах: как покупатель и как продавец. Очевидно, число продавцов и покупателей для разных товаров будет разным. Поэтому числа и не следует ассоциировать с числом продавцов и покупателей. В-третьих, доход каждого потребителя предполагается состоящим из двух компонент: 1) выручки от продажи принадлежащего ему начального запаса товаров
В модели Вальраса считается, что весь доход производственного сектора полностью распределяется между потребителями:
где В-четвертых, функции спроса В модели Вальраса понятия совокупных спроса и предложения формализуются следующим образом. Определение 4.1. Функцией совокупного (рыночного) спроса называется множественнозначная функция
Функцией совокупного (рыночного) предложения называется множественнозначная функция
При таком определении смысл совокупного спроса полностью соответствует способу формирования рыночного спроса на основе решений оптимизационных задач индивидуальных потребителей. Конкретно, это есть сумма индивидуальных функций спроса потребителей. Определение же функции совокупного предложения требует дополнительного пояснения. С этой целью введем обозначения:
По определению, любой элемент множества Y можно представить вектором Покажем, что для любого p
Рис. 4.4 Сумма вектора и множества Поэтому
и
Рассмотрим трех потребителей. Для любого
Продолжая эти рассуждения, получаем
Точно так же устанавливается включение Формализовав понятия функций совокупных спроса и предложения, модель рынка (4.3.1) можно представить совокупностью вида
Любой вектор Определение 4.2. Набор векторов
В этом случае По определению функций совокупных спроса и предложения, из включений (4.3.6) следует
т.е. совокупные спрос и предложение формируются как суммарные величины индивидуальных спросов потребителей и индивидуальных предложений производителей. Поэтому в развернутом виде условия равновесия (4.3.6)-(4.3.8) можно переписать в виде:
Рассмотрим экономическое содержание условий, определяющих конкурентное равновесие на рынке (4.3.5). Условие (4.3.6) показывает, что на цены
т.е. необходимость в условии (4.3.8) отпадает.
Рис. 4.5 Предложение с излишком
Предположим, что для некоторого товара в (4.3.7) имеет место строгое неравенство:
Следовательно, для восстановления условия (4.3.8) нужно ликвидировать излишек. С учетом знака
т.е. товар k вообще исключается из обращения на рынке. Обоснование справедливости (4.3.8) тем, что поставляемый сверх имеющегося спроса товар получает нулевую цену, экономически осмысленно, но не поддается адекватной формализации. Действительно, для фиксированного числа
несовместимо с равенством
Таким образом, формальный выход из рассматриваемой ситуации состоит в том, чтобы считать цену перепроизводимого товара равной нулю. Чисто теоретически этот прием состоятелен, так как не приводит в дальнейшем к противоречиям. В то же время, следует признать отсутствие экономически осмысленного объяснения существования товара с нулевой ценой. Объявление такого товара свободным представляется несостоятельным. Строго говоря, в экономике нет свободных товаров, любой побочный продукт может найти применение, т.е. имеет ненулевую цену. Нельзя согласиться и с хорошо известной экономистам модификацией закона спроса и предложения о существовании перепроизводимых товаров с нулевой ценой, поскольку в случае перепроизводства спрашиваемая часть этого товара продается по ненулевой цене. Для экономики существование излишек так же плохо, как и существование дефицита. Все это говорит в пользу целесообразности определения равновесия в виде (4.3.13) . Модель рынка по Вальрасу построена. Как видно, центральное место в ней занимает понятие конкурентного равновесия. Привлекательность равновесия как состояния рынка (и экономики в целом), заключается в возможности реализации всех произведенных товаров и в удовлетворении спроса всех потребителей. Процесс формирования рыночных цен условно можно сравнить с работой некоторого алгоритма, состоящего из четырех блоков (Рис. 4.6).
Рис. 4.6 Схема формирования равновесных цен
В первом блоке Утвердительный ответ на этот вопрос связан с разрешением двух важных проблем: 1. установление факта существования конкурентного равновесия в модели Вальраса; 2. разработка сходящейся к равновесной цене вычислительной процедуры (метода) формирования рыночных цен. Существование равновесия в модели Вальраса не установлено. Причина заключается в уровне формализма этой модели - она является весьма абстрактной. Конкретизируя определения составляющих ее элементов и уточняя их функциональные свойства, можно получить разные модификации модели Вальраса. Наиболее известная из них носит название модели Эрроу-Дебре, по именам ее создателей. Проблема разработки численных методов вычисления равновесных цен связана с установлением необходимых и достаточных признаков равновесия. Необходимо, чтобы они были конструктивными, т.е. порождали сходящуюся итеративную процедуру, какой является, например, паутинообразная модель (см. Рис. 4.2).
Поиск по сайту: |
 , где
, где  - число видов всех товаров. Компонентами вектора
- число видов всех товаров. Компонентами вектора 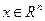 являются как выпуски, так и затраты (первичные факторы). Для различения их, затраты снабжают отрицательным знаком (поэтому записываем
являются как выпуски, так и затраты (первичные факторы). Для различения их, затраты снабжают отрицательным знаком (поэтому записываем 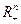 ). Если
). Если 
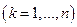 , индексы потребителей - буквой
, индексы потребителей - буквой 
 и индексы производителей - буквой
и индексы производителей - буквой 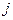
 . Через
. Через  обозначим вектор цен товаров.
обозначим вектор цен товаров. функцией дохода
функцией дохода  и вектор-функцией спроса на продукты производства
и вектор-функцией спроса на продукты производства 
 и вектор-функцией спроса на затраты
и вектор-функцией спроса на затраты  . Однако в модели Вальраса применяется несколько обобщенная характеристика производителя - с помощью одного множества
. Однако в модели Вальраса применяется несколько обобщенная характеристика производителя - с помощью одного множества  трактуемого как множество его (оптимальных) производственных планов. На языке «затраты-выпуск» это множество можно определить следующим образом:
трактуемого как множество его (оптимальных) производственных планов. На языке «затраты-выпуск» это множество можно определить следующим образом:  где
где  - производственная функция. Очевидно,
- производственная функция. Очевидно,  .
. (4.3.1)
(4.3.1) - пространство цен товаров, N - множество всех участников рынка (N содержит
- пространство цен товаров, N - множество всех участников рынка (N содержит  элементов).
элементов).
 содержит цены как товаров конечного потребления, так и затрат. Далее будем исходить из изменчивости цен. Причем цены меняются не по желанию отдельных участников рынка, а исключительно под воздействием совокупного спроса и совокупного предложения. Поэтому одним из ключевых является вопрос: существуют ли такие цены, которые устраивают как потребителей, так и производителей?
содержит цены как товаров конечного потребления, так и затрат. Далее будем исходить из изменчивости цен. Причем цены меняются не по желанию отдельных участников рынка, а исключительно под воздействием совокупного спроса и совокупного предложения. Поэтому одним из ключевых является вопрос: существуют ли такие цены, которые устраивают как потребителей, так и производителей? , 2) дохода, получаемого от его участия в прибыли производственного сектора (обозначим
, 2) дохода, получаемого от его участия в прибыли производственного сектора (обозначим 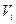 , например, посредством приобретения ценных бумаг и других видов инвестиционной и трудовой деятельности. Таким образом, мы предполагаем, что
, например, посредством приобретения ценных бумаг и других видов инвестиционной и трудовой деятельности. Таким образом, мы предполагаем, что / (4.3.2)
/ (4.3.2)
 , а скалярное произведение справа, с учетом структуры векторов
, а скалярное произведение справа, с учетом структуры векторов  , трактуется как прибыль всего производственного сектора. Заметим, что суммирование векторов
, трактуется как прибыль всего производственного сектора. Заметим, что суммирование векторов  и предложения
и предложения  предполагаются векторными и множественнозначными. Например, для функции
предполагаются векторными и множественнозначными. Например, для функции 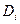 первое свойство означает, что
первое свойство означает, что  где
где  - скалярная функция спроса на
- скалярная функция спроса на  а множество таких векторов, т.е.
а множество таких векторов, т.е.  Это имеет место, например, когда в соотношении (2.5.2), определяющем спрос, максимум достигается не только в одной точке.
Это имеет место, например, когда в соотношении (2.5.2), определяющем спрос, максимум достигается не только в одной точке. (4.3.3)
(4.3.3) (4.3.4)
(4.3.4)


 , где
, где 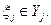 Так как
Так как  есть множество оптимальных планов производителя j, то компонентами вектора
есть множество оптимальных планов производителя j, то компонентами вектора  нельзя называть однозначно предложением. В то же время, вектор
нельзя называть однозначно предложением. В то же время, вектор  может быть интерпретирован как совокупное предложение, так как часть компонент вектора
может быть интерпретирован как совокупное предложение, так как часть компонент вектора  и
и  , т.е. областью изменения совокупных функций является то же самое пространство, что и для индивидуальных функций. Рассмотрим сначала двух потребителей. Для любого
, т.е. областью изменения совокупных функций является то же самое пространство, что и для индивидуальных функций. Рассмотрим сначала двух потребителей. Для любого  множество
множество  образуется смещением множества
образуется смещением множества  в направлении вектора x на длину этого вектора (Рис. 4.4).
в направлении вектора x на длину этого вектора (Рис. 4.4).


 множество
множество  образуется смещением множества
образуется смещением множества  в направлении вектора x на длину этого вектора. Поэтому
в направлении вектора x на длину этого вектора. Поэтому  и
и

 Так как
Так как  и потому
и потому  , то множество
, то множество  образуется смещением множества Y в направлении вектора b на длину этого вектора. Поэтому
образуется смещением множества Y в направлении вектора b на длину этого вектора. Поэтому 
 (4.3.5)
(4.3.5) называется совокупным спросом (соответствующим вектору цен p); любой вектор
называется совокупным спросом (соответствующим вектору цен p); любой вектор  - совокупным предложением (соответствующим вектору цен p). Эти векторы являются (оптимальными) реакциями совокупного покупателя и совокупного продавца на установившийся на рынке вектор цен. Если при этом
- совокупным предложением (соответствующим вектору цен p). Эти векторы являются (оптимальными) реакциями совокупного покупателя и совокупного продавца на установившийся на рынке вектор цен. Если при этом  , то на рынке возникает дефицит товаров, а при
, то на рынке возникает дефицит товаров, а при  , появляются их излишки. Такие цены не могут считаться удовлетворительными, так как в одном случае ущемлены интересы покупателей, а в другом - продавцов. Очевидно, наилучшим вариантом для экономики является равенство
, появляются их излишки. Такие цены не могут считаться удовлетворительными, так как в одном случае ущемлены интересы покупателей, а в другом - продавцов. Очевидно, наилучшим вариантом для экономики является равенство  . Этот идеальный случай на практике не всегда имеет место. Поэтому целесообразно как-то его ослабить. В модели Вальраса допускается наиболее гуманный с точки зрения интересов потребителей вариант обобщения понятия экономического равновесия.
. Этот идеальный случай на практике не всегда имеет место. Поэтому целесообразно как-то его ослабить. В модели Вальраса допускается наиболее гуманный с точки зрения интересов потребителей вариант обобщения понятия экономического равновесия. называется конкурентным равновесием на рынке (4.3.5) , если
называется конкурентным равновесием на рынке (4.3.5) , если 
 (4.3.6)
(4.3.6) (4.3.7)
(4.3.7) (4.3.8)
(4.3.8) называется равновесным вектором цен.
называется равновесным вектором цен. где
где 
 где
где 
 (4.3.10)
(4.3.10) (4.3.11)
(4.3.11) (4.3.12)
(4.3.12) (4.3.13)
(4.3.13)
 . Тогда в стоимостном выражении получаем неравенство
. Тогда в стоимостном выражении получаем неравенство 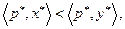 не соответствующее условию (4.3.8). Величина
не соответствующее условию (4.3.8). Величина  называется излишком. Согласно закону предложения, в случае появления излишка цена товара должна быть снижена. Но это приведет к изменению равновесной цены
называется излишком. Согласно закону предложения, в случае появления излишка цена товара должна быть снижена. Но это приведет к изменению равновесной цены  . Найдём способ выхода из этого противоречия? Очевидно,
. Найдём способ выхода из этого противоречия? Очевидно,
 это возможно только при
это возможно только при  Но тогда
Но тогда и
и 

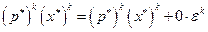 .
.
 формируется вектор цен. Информация о векторе p поступает в блоки
формируется вектор цен. Информация о векторе p поступает в блоки  и
и  , в которых формируются соответственно множества
, в которых формируются соответственно множества  и
и  , содержание которых, в свою очередь, передается в блок
, содержание которых, в свою очередь, передается в блок  . В блоке
. В блоке  . Если существует пара или пары
. Если существует пара или пары  , для которых выполняется условие
, для которых выполняется условие