 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Точки разрыва функции и их классификация
ГЛАВА 3 НЕПРЕРЫВНОСТЬ ФУНКЦИИ Определение непрерывности функции в точке С понятием предела функции тесно связано понятие непрерывности функции. Пусть функция
Рис. 3.1
Из рисунка видно, что, во-первых, в точке Таким образом, в точке
Определение. Функция
Данное равенство означает выполнение трех условий: 1. функция 2. функция 3. предел функции в точке
Для того, чтобы функция Когда
Это означает, что при нахождении предела непрерывной функции Для некоторых практических применений бывает полезно другое определение непрерывности функции, которое опирается на понятие приращения аргумента и функции (рис. 3.2).
Рис. 3.2
Пусть функция Приращение функции равно
Если
Следовательно,
Определение. Функция
Исследуя непрерывность функции в точке применяют, либо первое, либо второе определения.
3.2. Односторонняя непрерывность в точке. По аналогии с понятием предела функции слева (справа) вводится понятие непрерывности функции слева (справа). Пусть функция определена на полуинтервале Аналогично, если функция Для того, чтобы выполнялось условие непрерывности функции в точке
необходимо и достаточно, чтобы функция была непрерывна как слева, так и справа в этой точке. Пользуясь односторонними пределами, условие непрерывности можно заменить равносильным ему двойным равенством, т.е., поскольку
то
Таким образом, функция
Определение. Функция
Определение. Функция
Точки разрыва функции и их классификация Если в точке
Определение. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Точки разрыва функции классифицируются в зависимости от того, как именно нарушено двойное равенство
или являющееся условием непрерывности функции в точке. Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Определение. Точка разрыва
При этом 1) если 2) если
Рис. 3.3 Рис. 3.4
Определение. Точка разрыва
Рис. 3.5
Примеры Найти точки разрыва функций и определить их род. 1. Функция определена при всех значениях х, кроме
Функция в точке
2. Точкой разрыва для функции является точка
Поскольку левый и правый пределы при
3.4. Основные теоремы о непрерывных функциях. Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах. Приведем теоремы о непрерывных функциях без доказательств.
Теорема. Сумма, разность, произведение и частное двух непрерывных функций есть функция непрерывная (для частного − делитель отличен от нуля).
Теорема. Сложная функция, составленная из конечного числа непрерывных функций, непрерывна.
Теорема. Функция, обратная к монотонной и непрерывной на интервале
Для основных элементарных функций (п.1.7), справедлива следующая теорема.
Теорема. Всякая основная элементарная функция непрерывна в каждой точке, в которой она определена.
Подавляющее большинство функций, которые рассматриваются в математике, являются элементарными. Опираясь на определение элементарной функции (§1.10), непрерывность основных элементарных функций, а также на приведенные выше теоремы можно утверждать, что всякая элементарная функция непрерывна в ее области определения.
Поиск по сайту: |
 определена в точке
определена в точке  и в некоторой окрестности этой точки. Чтобы уяснить понятие непрерывности, рассмотрим точку
и в некоторой окрестности этой точки. Чтобы уяснить понятие непрерывности, рассмотрим точку 
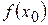 . Во-вторых, если
. Во-вторых, если 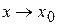 , то
, то  (независимо от того, как
(независимо от того, как 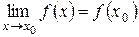 .
. определена в точке
определена в точке 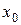 и в ее окрестности;
и в ее окрестности; ;
; , и равенство (1) можно записать в виде
, и равенство (1) можно записать в виде .
.
 функция принимает значение
функция принимает значение 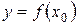 , а при
, а при  , соответственно,
, соответственно, 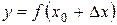 .
. .
. , тогда
, тогда .
.
 , и в точке
, и в точке  . Если этот предел равен значению функции в точке
. Если этот предел равен значению функции в точке 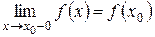 или
или 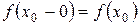 , то эту функцию называют непрерывной слева в точке
, то эту функцию называют непрерывной слева в точке  определена на полуинтервале
определена на полуинтервале 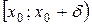 и
и  или
или  , то эту функцию называют непрерывной справа в точке
, то эту функцию называют непрерывной справа в точке 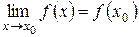 ,
, ,
, .
. , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала. , если она непрерывна в интервале
, если она непрерывна в интервале  непрерывна справа, т.е.
непрерывна справа, т.е. 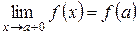 , а в точке
, а в точке 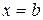 непрерывна слева, т.е.
непрерывна слева, т.е.  .
. , или
, или  при произвольном стремлении
при произвольном стремлении  функция
функция  ,
, .
.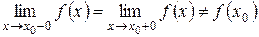 , то
, то  , то
, то 

 ;
;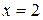 . Найдем пределы функции слева и справа в точке
. Найдем пределы функции слева и справа в точке  ;
; .
. ;
; . Вычислим левый и правый пределы функции при
. Вычислим левый и правый пределы функции при  .
. ;
; .
. .
.