 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
концентрации тепловых дефектов
Термодинамическая И экспериментальная оценка концентрации тепловых дефектов
Полученные выше соотношения показывают, что концентрация тепловых дефектов может быть рассчитана для любой температуры, если известны теплота образования дефекта и колебательная энтропия. Наибольшую трудность представляет определение колебательной энтропии, поэтому при получении оценочных данных этой величиной пренебрегают, полагая, что в уравнениях (2.8), (2.14), (2.16) предэкспоненциальный множитель может быть взят равным единице. Теплота образования теплового дефекта может быть оценена по закону Гесса. Пусть в бинарном кристалле АВ стехиометрического состава при тепловом воздействии на него возникают тепловые дефекты по Шоттки. Мысленно этот процесс можно разделить на две стадии: – разрыв связей частиц в объеме кристалла и удаление их в бесконечность. В этом случае в каждой из подрешеток кристалла – катионной и анионной – остается по одной вакансии.
(AB)N = AN-1BN-1 + VA +VB + Aгаз + Bгаз+ DH1, (3.1)
где N – общее число частиц в кристалле; VA и VB – вакансии, соответственно в катионной и анионной подрешетках; DH1 – теплота этого процесса; – конденсация высвободившихся частиц на поверхности кристалла. Это приводит к достраиванию кристалла и увеличению числа катионных и анионных узлов решетки.
AN-1BN-1 + Aгаз + Bгаз = (AB)N – DH2, (3.2)
где DH2 – теплота конденсации обеих частиц на поверхности кристалла. Суммируя уравнения, получаем 0 = VA + VB + DH1 – DH2.
Таким образом, теплота образования пары тепловых дефектов равна алгебраической сумме DHдеф = DH1 – DH2 . Можно допустить, что по абсолютной величине теплота DH2 приблизительно вдвое меньше, чем DH1. Действительно, если уравнение (3.2) записать в обратном порядке, получим
(AB)N = AN-1BN-1 + Aгаз + Bгаз + DH2. (3.3)
Эта реакция характеризует испарение, не сопровождающееся образованием вакансий внутри кристалла, что возможно при удалении частиц только с поверхности. А так как у поверхностных частиц приблизительно половина связей оборвана, то DH2 » 0.5DH1. Тогда DHдеф = 2DH2 – DH2 = DH2. Процесс (3.3) иногда называют атомизацией, а теплоту DH2 – теплотой атомизации, она приблизительно равна теплоте образования дефекта Шоттки. Эта теплота может быть найдена по закону Гесса, если реакцию атомизации представить в виде следующего термохимического цикла:
АВтв = Атв + Втв – DHАВ
Атв = Агаз + DHАгаз
Втв = ½ В2газ+ ½ DHВ2газ
½ В2газ = Вгаз + ½ DHВ ____________________________________ DHат = -DHАВ + DHАгаз + ½ DHВ2газ + ½ DHВ
Здесь DHАВ – теплота образования АВтв из элементов; DHАгаз и DHВ2газ – теплоты возгонки А и В, DHВ – теплота диссоциации. Оценим погрешность, которая получится, если такие расчеты теплот образования тепловых дефектов будут использованы для определения концентрации этих дефектов. Для этого оценим вклад колебательной энтропии в эту величину. Пусть в элементарном кристалле при беспорядке по Шоттки n/n1 = 1,5. Для многих элементарных кристаллов эта величина близка к истинному значению. Тогда при р = 8 (кубическая объемно-центрированная решетка) предэкспоненциальный множитель в уравнении (2.8) составит (1,5)8 » 25. Это и есть искомая погрешность. Для оценочных расчетов она не так уж велика, так как это означает, что если термодинамический расчет показывает такой уровень теплового беспорядка, когда, например, одна вакансия приходится на один миллион частиц, расположенных в регулярных узлах, то в действительности в этом миллионе узлов окажется не одно, а двадцать пять вакантных мест. Для экспериментального определения концентрации тепловых дефектов выбирают такое свойство кристалла, где связь «свойство – концентрация» является близкой к линейной. Таким свойством является тепловое расширение кристаллов. При тепловом разупорядочении по Шоттки происходит увеличение объема кристалла. Поскольку у частиц, расположенных на поверхности кристалла, меньше соседей и их связь с кристаллом ослаблена, именно с них должен начаться процесс разупорядочения при тепловом воздействии на кристалл. Правда тепловое расширение кристалла происходит и тогда, когда вакансий в нем еще нет, но в этом случае выполняется соотношение
где V – объем кристалла; l – длина кристалла. В свою очередь, для кубической решетки выполняется равенство
где Dl = lT – l – изменение длины кристалла; Da = aT – a – изменение параметра решетки при тепловом воздействии на кристалл. Когда в кристалле появляются тепловые дефекты, равенство (3.5) не соблюдается. Тогда Dl/l > Da/a, а разность
где N – число атомов в кристалле; n – число вакансий. В действительности частицы, ушедшие из своих узлов, занимают новые узлы на поверхности кристалла, достраивая его. Тогда получим, что DV = na3 – nfa3 = na3(1 – f). Относительное увеличение объема кристалла можно записать в виде
Подставляя в (3.4), получим
Чтобы выразить значение коэффициента f через относительное изменение параметра решетки, воспользуемся тем, что для мнимого относительного уменьшения объема кристалла, характеризуемого (3.6), справедливы соотношения (3.4) и (3.5), тогда
Подставляя (3.9) в (3.8), получим
откуда
где n/N – атомная доля вакансий в кристалле. Таким образом, концентрация тепловых дефектов по Шоттки в кристалле с кубической решеткой равна утроенной разности между относительным изменением длины кристалла и относительным изменением параметра его решетки. Обе величины (a и l) доступны для измерения с такой точностью, которая позволяет проводить определение концентрации тепловых дефектов, когда их атомная доля достигает значения 10-5. Изложенный способ позволяет рассчитать все термодинамические параметры процесса теплового разупорядочения. Так как N >> n, то
Тогда можно определить энергию Гиббса образования тепловых дефектов при температуре Т.
Если разность 3(Dl/l – Da/a) измерена при двух температурах, это дает возможность вычислить также энтальпию и энтропию образования тепловых дефектов. Если принять, что температурную зависимость DG = f(T) можно приближенно представить в виде линейной зависимости, то есть DG = a + bT, то, измерив n/N при двух температурах, можно вычислить коэффициенты a и b из системы уравнений DGT1 = a + bT1, DGT2 = a + bT2 . Тогда можно считать, что DH = a, DS = –b.
Поиск по сайту: |
 (3.4)
(3.4) (3.5)
(3.5) пропорциональна концентрации вакансий в кристалле. При разупорядочении по Шоттки образовавшаяся вакансия сжимается соседями, вследствие чего усредненный параметр решетки становится меньше того, который был бы в кристалле без вакансий. DVяч = –f a3, где f – поправочный коэффициент, учитывающий сжатие. То есть, если бы частицы, ушедшие из узлов, покидали кристалл, то его объем должен был бы уменьшаться.
пропорциональна концентрации вакансий в кристалле. При разупорядочении по Шоттки образовавшаяся вакансия сжимается соседями, вследствие чего усредненный параметр решетки становится меньше того, который был бы в кристалле без вакансий. DVяч = –f a3, где f – поправочный коэффициент, учитывающий сжатие. То есть, если бы частицы, ушедшие из узлов, покидали кристалл, то его объем должен был бы уменьшаться. , (3.6)
, (3.6) (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9)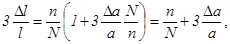
 (3.10)
(3.10)
 .
.