|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрическая алгебра древних греков.
Муниципальное общеобразовательное учреждение лицей № 8 “Олимпия” Дзержинского района г.Волгограда
Геометрический способ решения Квадратных уравнений
Выполнил: учащийся 8 “В” класса лицея № 8 “Олимпия” Цепляев Никита. Научный руководитель: Кокиева Л.Д., учитель математики
Волгоград, 2009 г. Квадратным уравнением называется уравнения вида ах2+bx+c=0, где а,b,c-действительные числа и а≠0. Если а =1, то квадратное уравнение называется приведённым, если а≠1-неприведенным. Существует множество способов решения квадратных уравнений. Франсуа Виет родился в 1540 году во Франции, в Фонтене –ле – Конт. По образованию юрист. Он много занимался адвокатской деятельностью, а с 1571 год по 1584 год был советником короля Георга III и Георга IV. Но всё свободное время, весь свой досуг он отдавал занятиям математикой. Особенно усиленно он начал работать в области математики с 1584 год, после отстранения от должности при королевском дворе. Виет детально изучил труды как древних, так и современных ему математиков и создал по существу новую алгебру. Он ввёл в неё буквенную символику. После открытия Виета, стало возможным записывать правила в виде формул. Именно с 1591 года мы пользуемся формулами при решении квадратных уравнений. О геометрических способах известно мало. Попробуем систематизировать весь известный материал. Впервые квадратные уравнения сумели решить математики Древнего Египта. В одном из математических папирусов содержится задача: «Найти стороны поля, имеющие форму прямоугольника, если его площадь 12, а 3/4 длины равны ширине». Рассмотрим её. Пусть х - длина поля. Тогда 3х/4- его ширина. S=3х2/4-площадь. Получилось квадратное уравнение.
В папирусе дано правило для его решения: «Раздели 12 на 3/4». 12: Итак х2=16. «Длина поля равна 4»-указано в папирусе. Геометрическая алгебра древних греков. Греки считали, что величины можно представить в виде отрезков, прямоугольников (произведение двух величин-отрезков) и прямоугольных призм (произведение трёх величин-отрезков). При таком подходе арифметической операции над величинами также приобретали геометрический смысл. Результат сложения или вычитания отрезков представлял собой отрезок, прямоугольников (после соответствующего преобразования)- прямоугольник, а призм - призму. Иными словами, операция сложения и вычитания не выводили за приделы рассматриваемого класса величин. С умножением и делением величин положение обтаяло иначе. Произведением величин - отрезков а и b являлся прямоугольник со сторонами а и b, а произведением прямоугольник и отрезка – прямоугольная призма. Однако операция деления, обратная операция умножению, оказывалось, возможно, только тогда, размерность делимого была выше размерности делителя. Скажем, величину, представленную прямоугольником, можно было разделить на величину-отрезок, но отрезок на отрезок разделить было нельзя. Пусть требуется разделить величину, представленную прямоугольником со сторонами а и b, на величину-отрезок с Частным от деления должен быть такой отрезок х, что прямоугольник со сторонами с и х был бы равен прямоугольнику со сторонами а и b. Геометрически задача сводится к построению прямоугольника с заданной стороной с, который по площади равен прямоугольнику со сторонами а и b. На (рис.1) показано как можно построить такой прямоугольник. Достаточно продолжить сторона а данного прямоугольника на величину с и достроить чертёж до прямоугольника АВСD. Получившийся под диагональю прямоугольник и является искомым.
(рис.1)
A D
C помощью геометрической алгебры греки не только доказывали алгебраические тождества, но и решали некоторые виды квадратных уравнений, такие, как: x2=ab (1) x(a-b)=b2 (2) x(a+b)=b2 (3) где a и b – заданные величины. Рассмотрим сначала уравнение x2=ab. Геометрически его можно сформулировать следующим образом: найти такой отрезок х, что площадь построенного на нём квадрата равна площади прямоугольника, построенного на заданных отрезках а и b. Иными словами, требуется преобразовать заданный прямоугольник в квадрат. Представив правую часть уравнения с помощью формулы в виде разности квадратов, получим уравнение:
Так как величины х, cвязаны соотношением для сторон прямоугольного треугольника (по теореме Пифагора), то проблема сводится к нахождению катета х прямоугольного треугольника, гипотенуза и второй катет которого известны. Геометрическое решение этой задачи несложно: на отрезке полуокружность, а затем найти на ней точку, отстоящую от одного из концов отрезка на величину Уравнение можно решить и другим способом. На отрезке a+b как на диаметре построим полуокружность. Затем из общего конца отрезков а и b поставим перпендикуляр к диаметру до пересечения с полуокружностью. Длина этого перпендикуляра и будет искомой величиной х. Хотя это решение является геометрическим, оно использует методы не геометрической алгебры, а теории пропорций. Перейдём к уравнению (2). Переведём его на язык геометрии: К отрезку AD=а приложить прямоугольник ACFL, равновеликий данному квадрату (b2), так, чтобы фигура CDMF, дополняющая прямоугольник ACFL до прямоугольника ADML, была квадратом с площадью x2. Предложим, что построение выполнено. Из (рис. 4)нетрудно заметить, что площадь фигуры BDHGFE, где – В – середина AD, равна площади прямоугольника ACFL. Тогда площадь прямоугольника ACFL равна выражению, стоящему в левой части уравнения, т.е. х(а-х). равенство площадей прямоугольника ACFL и фигуры BDHGFE, получим
Поскольку площадь прямоугольника ACFL равна b2, верно равенство
Оно связывает условием теоремы Пифагора три величины: Геометрически это означает, что существует прямоугольный треугольник с гипотенузой Так как величины гипотенузы и одного из катетов известны, то нетрудно построить другой катет. Определив величину A B C D
(рис.4) BD= L M M
K G H
Арабская алгебра. Арабская алгебра стала самостоятельной дисциплиной в IXXв. Основной вклад в её становление внесли математики ал-Хорезми и Абу-Камил (ок. 850-930). При решении и исследовании уравнений использовались разнообразные арифметические способы и геометрические методы. Так, например, ал-Караджи ввёл арифметические операции над одночленами и выражениями, составленными из них, тем самым заложив фундамент алгебры многочленов. Лишь операции деления он ограничивал делением многочлена на одночлен. Алгебраический трактат ал-Хорезми был задуман руководство для решения практических задач, в том числе о справедливом разделе наследства. В мусульманском праве существовала сложная система наследования, в соответствии которой свою долю в зависимости от степени родства должны были получить многочисленные родственники умершего. Для решения этой задачи решались квадратные уравнения. В отличии от совместной алгебры ал-Хорезми не рассматривал общего решения квадратного уравнения. Его интересовали только частные случаи. Поскольку население не может быть отрицательным числом, ал-Хорезми совершенно избегал уравнений, у которых нет ни одного положительного корня. Другая особенность касались системы записи уравнений. Ал-Хорезми записывал уравнение так, чтобы среди входящих в его левую и правую части членов были лишь слагаемые, но не вычитаемые. Вследствие указанных ограничений ему приходилось рассмотривать отдельно следующие канонические уравнения, к которым с помощью алгебраических преобразований «ал-джабр» и «ал-мукабала» приводили другие уравнения: 1) ах2=bx (в терминологии ал-Хорезми – «квадраты равны корням»); 2) ах2=с («квадраты равны числу»); 3) ах=с («корни равны числу»); 4)ax+bx=c («квадраты и корни равны;числу»); 5)ax2+c=bx («квадраты и числа равны числу»); 6)bx+c=ax2 («корни и числа равны квадратам»). Часто кроме алгебраического решения (будучи выражено в алгебраической символике, оно аналогично современному) ал-Хорезми предлагал наглядно – геометрическое. Вот так он решал геометрически уравнение относящееся к четвёртому типу. Х 2+10Х=39 Сначала возьмём квадрат, сторону которого обозначим через х. Его площадь равна х2 (рис.5)
На сторонах квадрата построим четыре прямоугольника со сторонами, равными х и 10/4 ;полученную фигуру Площадь каждого из четырёх угловs[ квадратов со сторонами 10/4 равна 100/16=6 1/4 , а их сумма составляет 100/4=25.
Наконец, из равенства х+2*10/4=8 находим значение х=3. Методы решения квадратных уравнений были известны еще в древние времена. Они излагались в вавилонских рукописях царя Хаммурапи (ХХ в. до н.э.), в трудах древнегреческого математика Евклида (III в. до н.э.), в древних китайских и японских трактатах. Многие математики древности решили квадратные уравнения геометрическим способом: квадрат и 10 его корней равны 39. Для решения уравнения x2 + 10x = 39 поступали следующим образом. Пусть AB = x, BC = 5, (10:2). На стороне АС = АВ + ВС строился квадрат, который разбивался на четыре части, как показано на рисунке. Очевидно, что сумма площадей I, II, III частей равна x2 + 10x или 39. Если к этой площади прибавить площадь IV части, то 39 + 25 = 64 – площадь всего квадрата. Но эта же площадь равна (x +5)2. Следовательно, (x + 5)2 =64. x +5 =8, x = 3.Таким образом, число 3 является корнем квадратного уравнения, ведь отрицательных чисел тогда не знали.
А вот как решал эту же задачу ал-Хорезми в 825 году. Строим квадрат со стороной x и на его сторонах – четыре прямоугольника высотой x2 + 4∙ x + 2∙ Решение квадратных уравнений с помощью циркуля и линейки.
Предлагается следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис.). Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA; 3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
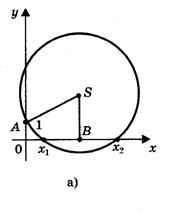
При этом возможны три случая. 1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис.,а) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.
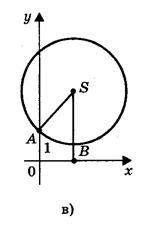
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис.,в), в этом случае уравнение не имеет решения.
• Пример.
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1). Ответ: х1 = - 1; х2 = 3.
Поиск по сайту: |
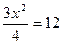
 =12
=12 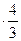 =16
=16 В С
В С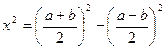
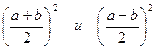 , входящие в уравнение,
, входящие в уравнение,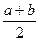 как на диаметре надо построить
как на диаметре надо построить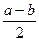 .соединив эту точку с другим концом отрезка, получим стороны искомой длины.
.соединив эту точку с другим концом отрезка, получим стороны искомой длины. Площадь фигуры BDHGFE равна разности площадей двух квадратов: большого со стороной ВD=
Площадь фигуры BDHGFE равна разности площадей двух квадратов: большого со стороной ВD= 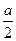 и малого со стороной EF=
и малого со стороной EF= 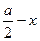 . Записав
. Записав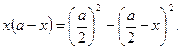
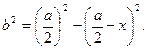
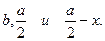

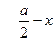 , легко найти искомую величину х.
, легко найти искомую величину х.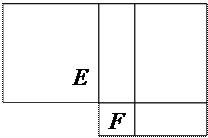
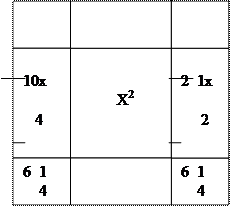
 достраиваем до квадрата. Площадь каждого из четырёх прямоугольников равна 10х/4 , а их сумма составляет 10х.
достраиваем до квадрата. Площадь каждого из четырёх прямоугольников равна 10х/4 , а их сумма составляет 10х. Если сложить величину площади внутреннего квадрата (х2) и сумму площадей четырёх прямоугольников (10х), то получится выражение х2+10х, представляющая собой левую часть уравнения. Площадь большого квадрата превосходит величину х2 +10х на 25. Так как из уравнения следует, что х2+10х = 39, то площадь большого квадрата равна 39+25=64, а его сторона равна 8. С другой стороны, из (рис. 5) видно, что сторона внешнего квадрата равна х+2*10/4.
Если сложить величину площади внутреннего квадрата (х2) и сумму площадей четырёх прямоугольников (10х), то получится выражение х2+10х, представляющая собой левую часть уравнения. Площадь большого квадрата превосходит величину х2 +10х на 25. Так как из уравнения следует, что х2+10х = 39, то площадь большого квадрата равна 39+25=64, а его сторона равна 8. С другой стороны, из (рис. 5) видно, что сторона внешнего квадрата равна х+2*10/4.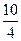 . В углах фигуры построим четыре квадрата со стороной
. В углах фигуры построим четыре квадрата со стороной 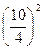 = x2 + 10x +
= x2 + 10x + 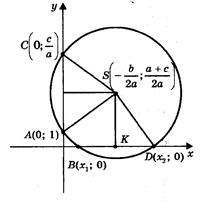 Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.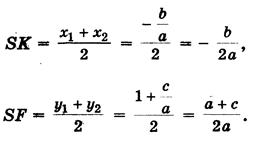
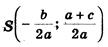 Итак:
Итак: 2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.,б) в точке В(х1; 0), где х1 - корень квадратного уравнения.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.,б) в точке В(х1; 0), где х1 - корень квадратного уравнения.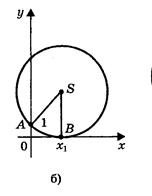
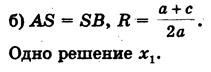
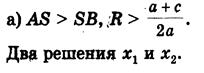

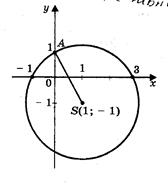 Решим уравнение х2 - 2х - 3 = 0 (рис.).
Решим уравнение х2 - 2х - 3 = 0 (рис.).