 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІСтр 1 из 2Следующая ⇒
Л.І. Колодій, О.О. Чупринін
Методичні вказівки до самостійної роботи та виконання розрахунково-графічних і практичних завдань з курсу будівельної механіки
„Розрахунок тришарнірних арок і рам”
(для студентів 2 і 3 курсу денної і заочної форм навчання за напрямом підготовки 0921 – «Будівництво» з професійного спрямування «Міське будівництво та господарство», “Теплогазопостачання і вентиляція”).
Харків – ХНАМГ – 2008 Методичні вказівки до самостійної роботи та виконання розрахунково-графічних і практичних завдань з курсу будівельної механіки “Розрахунок тришарнірної арки і рами” (для студентів 2-3 курсу денної і заочної форми навчання за напрямом підготовки 0921 – «Будівництво» з професійного спрямування «Міське будівництво та господарство», “Теплогазопостачання і вентиляція”). /Укл. Колодій Л.І., Чупринін О.О. – Харків: ХНАМГ, 2008. − 19 с.
Укладачі: Л.І. Колодій, О.О. Чупринін
Рецензент: завідувач кафедри теплохолодопостачання проф. М.О. Шульга
Рекомендовано кафедрою теоретичної і будівельної механіки, протокол № 1 від 30.08.08
ВСТУП
Ці методичні вказівки призначені для самостійної роботи студентів при підготовці до практичних занять і виконанні розрахунково-графічного завдання. Вони містять теоретичні положення, вихідні дані для завдання і приклади його виконання. Призначені для студентів денної і заочної форм навчання. У методичних вказівках розглядаються тришарнірні арки і рами, які є розпірними системами. Розпірною називають систему, в якій при вертикальному навантаженні, крім вертикальних, з'являються горизонтальні реакції – розпір. Аркою називають брус малої кривизни, кінці якого закріплені від взаємних лінійних зсувів. Рама являє собою систему стержнів, з’єднаних між собою переважно жорстко. Розрахункову схему у вигляді плоскої рами звичайно обирають при розрахунку поперечника промислової або цивільної споруди. Результатом розрахунку арки чи рами є епюри внутрішніх зусиль: згинаючих моментів – М, поперечних сил – Q і поздовжніх сил – N. Перш ніж приступити до виконання завдання, слід ознайомитися з теоретичним матеріалом, викладеним у главах 9 [1], главі 4 [2], і в п. 2 цих вказівок. Крім того, слід розібрати приклади розрахунку, наведені в [1] і [3]. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Брус з криволінійною віссю малої кривизни, наведений на рис. 1-3, є балочною системою, яку називають аркою. На відміну від простої двохопорної балки в такому брусі від вертикального навантаження з'являються значні горизонтальні опорні реакції. Ці реакції називають розпором, а системи, в яких вони з'являються, розпірними. Рами теж відносяться до розпірних систем.
Рис. 1
Розпір створює в перерізі арки чи рами момент, протилежний за знаком моменту вертикальних сил. За рахунок цього згинаючі моменти в розпірних системах зменшуються порівняно з балками, тому що деформація згину поєднується з деформацією стиску, що робить ці системи більш економічними. Арку, показану на рис. 1,а, називають двошарнірною. Така арка один раз статично невизначна. Якщо опори арки защемлені (рис. 1,б), арка називається безшарнірною, вона тричі статично невизначна. Арка, наведена на рис. 2, називається тришарнірною. Вона статично визначна. Розглянемо такі арки і рами. Точки обпирання арки називають п’ятами, точку, найбільш віддалену від опор (С) - замком. Найкоротшу відстань від лінії, що з'єднує опори, до замка називають стрілою підйому арки і позначають
Рис. 2
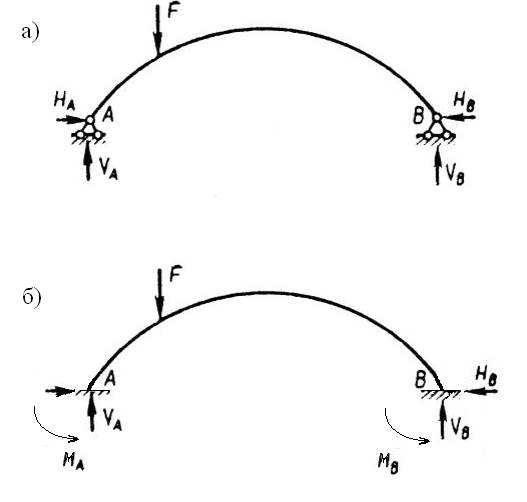
Визначення опорних реакцій. Ці реакції мають вертикальні й горизонтальні складові (рис. 3,а). З умови
Для визначення вертикальних складових реакцій використовують ті ж рівняння, що і в балці на двох опорах:
звідки
і
тоді
де Реакції Для визначення розпору використовують умову рівності нулю згинаючого моменту в проміжному шарнірі С (замку). Цей момент можна записувати для лівих або правих сил:
Наприклад, для правих сил знаходимо
З одержаного рівняння легко визначити розпір. Звернемо увагу на те, що усі члени лівої частини рівняння (5), крім складової від розпору, являють собою балочний згинаючий момент
У цьому виразі і надалі індекс
Рис. 3
Розглянемо обчислення внутрішніх зусиль у довільному перерізі Визначаємо згинаючий момент у перерізі
Одержуємо
де Рівняння (7) підтверджує, що згинаючі моменти в арці менші, ніж у балці. Різниця в згинаючих моментах визначається наявністю моменту, створеного розпором. Можна вирішити питання про окреслення осі арки за законом, при якому згинаючі моменти в усіх її перетинах дорівнюють нулю. Знаходимо з (7), що цей закон відповідає рівнянню
яке пропорційне балочному згинаючому моменту. Така арка називається раціональною. Наприклад, при дії рівномірно розподіленого вздовж прольоту навантаження
Для визначення поперечної і поздовжньої сил у перерізі
У наведених рівняннях складові, взяті в дужки, дорівнюють поперечній силі в перерізі балки
З рівняння (9) видно, що поздовжні сили в арці при дії вертикального навантаження завжди стискаючі. Епюри внутрішніх зусиль в арці Для параболічної арки з віссю, окресленою за рівнянням
а потім Для циркульної арки, вісь якої окреслена по дузі кола
початок координат на лівій опорі, де
Розрахунок тришарнірної рами відрізняється від розрахунку інших рам лише визначенням опорних реакцій. Їх знаходять з рівнянь рівноваги, аналогічних рівнянням рівноваги тришарнірної арки. Епюри внутрішніх зусиль будують на осях рами. Для розрахунку тришарнірної рами на вертикальне навантаження внутрішні зусилля можуть бути визначені за формулами (7 - 9). Для тришарнірної рами ординати й необхідні для розрахунків кути нахилу стержнів рами, які співпадають з нахилом дотичної до них, визначають безпосередньо із схеми рами.
Поиск по сайту: |

 . Вісь арки найчастіше приймають окресленою за параболою або дугою кола. Арки в цьому випадку називають відповідно параболічними й циркульними.
. Вісь арки найчастіше приймають окресленою за параболою або дугою кола. Арки в цьому випадку називають відповідно параболічними й циркульними.
 виходить, що горизонтальні складові опорних реакцій (розпір) арки при вертикальному навантаженні дорівнюють одна одній:
виходить, що горизонтальні складові опорних реакцій (розпір) арки при вертикальному навантаженні дорівнюють одна одній: (1)
(1)
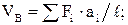 (2)
(2)
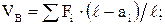 (3)
(3) і
і  - сили та координати їх місця дії відповідно (рис. 3,а).
- сили та координати їх місця дії відповідно (рис. 3,а).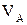 й
й 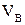 цілком відповідають опорним реакціям простої балки того ж прогону при тому самому навантаженні (рис. 3,б). Тому ці реакції називають балочними.
цілком відповідають опорним реакціям простої балки того ж прогону при тому самому навантаженні (рис. 3,б). Тому ці реакції називають балочними. або
або  . (4)
. (4)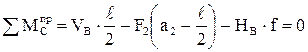 . (5)
. (5) у перерізі С (рис. 3,б). Таким чином, одержуємо залежність
у перерізі С (рис. 3,б). Таким чином, одержуємо залежність (6)
(6) означає, що відповідна величина визначена для балки. Звідси виходить, що розпір зменшується при збільшенні стріли підйому.
означає, що відповідна величина визначена для балки. Звідси виходить, що розпір зменшується при збільшенні стріли підйому.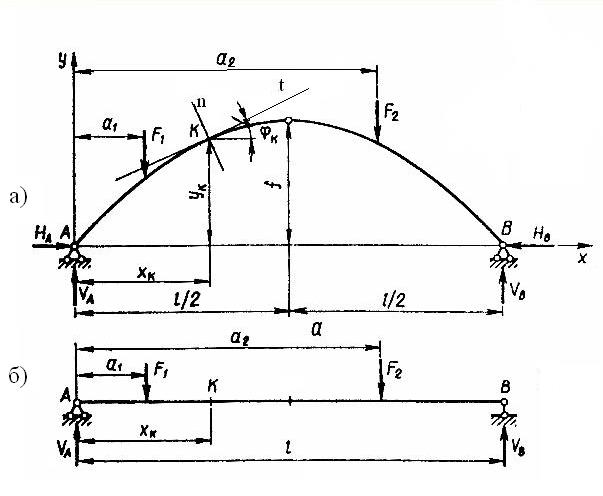
 з координатами
з координатами  і
і  (рис. 3,а).
(рис. 3,а). .
. , (7)
, (7) .
. ,
, отримуємо рівняння осі арки за параболічним законом:
отримуємо рівняння осі арки за параболічним законом: .
. (рис. 3,а).
(рис. 3,а).
 .
.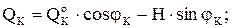 (8)
(8) . (9)
. (9) і
і  змінюються за нелінійними законами (7 - 9). Для побудови епюр арку розбивають уздовж осі х на рівні відрізки довжиною
змінюються за нелінійними законами (7 - 9). Для побудови епюр арку розбивають уздовж осі х на рівні відрізки довжиною 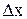 . Обчисливши в одержаних таким чином перерізах внутрішні зусилля
. Обчисливши в одержаних таким чином перерізах внутрішні зусилля  , початок координат розташований на лівій опорі, визначають
, початок координат розташований на лівій опорі, визначають , (10)
, (10) і
і  .
. , (11)
, (11) ;
;  . (12)
. (12)