|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные геометрические размеры антенны.
Эффективная площадь антенны будет равна:
Найдем общую площадь антенны:
где КИП, это коэффициент использования поверхности (Возьмем КИП=0.7). Следовательно, получаем что:
Для реализации ΔΘЕ=2
Тогда В плоскости вектора Н выберем угол засветки φ=600 Найдем фокус антенны:
В декартовой системе координат параболоид вращения определяется уравнением (начало координат совпадает с вершиной параболоида) x2=4fz Найдем глубину зеркала:
где X=L/2, а Z есть расстояние от края зеркала до облучателя.
Расстояние от облучателя до раскрыва антенны:
Рис. 5 Геометрические размеры антенны.
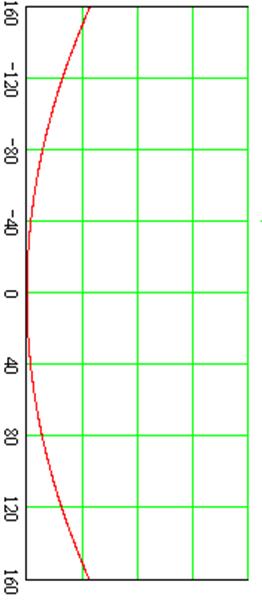
Рассчитаем профиль зеркала в программе Mathcad как функцию:
Рис. 6 раскрыв зеркала в плоскости Н .
Расчет амплитудного распределения (АР) в раскрыве зеркала Для полученных размеров антенны и ДН облучателя рассчитываем в программе Mathcad по следующей формуле: g(θ)=Fобл(θ)cos2(θ/2), где Fобл(θ)=cos1.66(θ), т.к. -10 = 20lgX lgX = -0.5
cosn(60) = 0.316 , откуда n = 1.66 Чтобы представить АР как функцию координаты плоского раскрыва, воспользуемся уравнением параболы x2=4fz, откуда x2=560z. R=L/2=160 мм. Возьмём 5 значений x, которые равны: 0.2R, 0.4R, 0.6R, 0.8R, R, т.е.: 32, 64, 96, 128, 160 Поочерёдно подставляя их в формулу
Используя программу Rektangl найдем АР:
Используя программу Rektangl,найдём аппроксимацию АР. При этом я выбрал следующие значения весов:
р1= 0.245 – равномерное АП р2= 0 – перевёрнутое параболическое АП р3= 0.41– косинусоидальное р4= 0 – перевёрнутое параболическое во второй степени АП р5= 0.2 – косинусоидальное во второй скорости АП p6= 0.145 – треугольное АП АР в плоскости вектора H и его аппроксимация:
,где красной линией показана аппроксимация.
Таблица значений:
КИП=0,891 Как уже было сказано выше, АР для плоскости вектора Е будет равномерным. Поэтому КИП=1 Среднее значение: КИП=0,9455
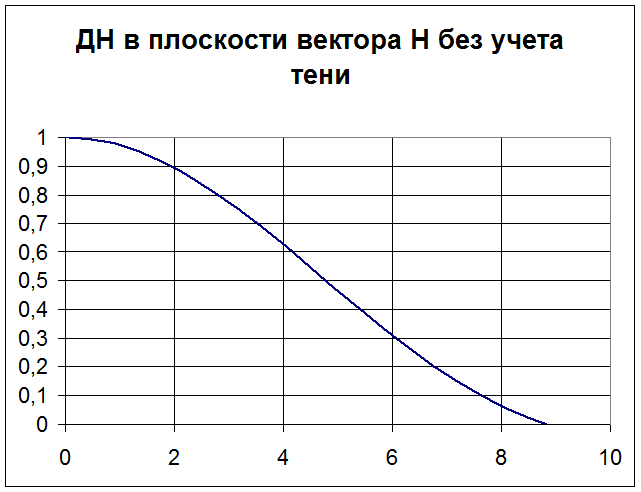
Расчет ДН без учета тени.
ДН является линейной комбинацией соответствующих парциальных ДН (Fi) с теми же весами, умноженными на параметр амплитудного распределения (Mi),
Для расчета ДН без учета тени в плоскости вектора Н воспользуемся программой Rektangl:
Таблица значений:
Ширина ДН по уровню 0,707 ΔΘH=6,33
Для плоскости вектора Е:
Т.к. в данной плоскости равномерное распределение, то ДН будет иметь вид:
Таблица значений:
Ширина ДН по уровню 0,707 ΔΘЕ=1,96
Поиск по сайту: |

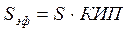


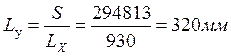


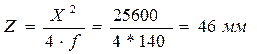






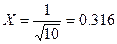
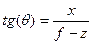 , где f- фокус антенны, вычисляем значения АР, для соответствующих углов, по формуле
, где f- фокус антенны, вычисляем значения АР, для соответствующих углов, по формуле 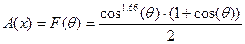 .
.

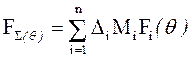 .
.