 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Краткие теоретические сведения. ИССЛЕДОВАНИЕ АНТЕННЫСтр 1 из 2Следующая ⇒
ИССЛЕДОВАНИЕ АНТЕННЫ С ЛОГАРИФМИЧЕСКОЙ ПЕРИОДИЧЕСКОЙ СТРУКТУРОЙ Общие методические указания В авиационном РЭО довольно часто используются антенны диапазонные и широкодиапазонные. При техническом обслуживании таких антенн возникает необходимость в проверке стабильности параметров в диапазоне частот. Одной из таких характерных антенн, которая работает в диапазоне частот, является антенна с логарифмической периодической структурой (логарифмическая антенна). Её входное сопротивление с некоторой периодичностью повторяется в рабочем диапазоне. Особенностью измерения входного сопротивления 8той антенны в данной лабораторной работе является использование измерительной линии и круговой диаграммы полных сопротивлений. Овладение навыками подобных измерений позволит будущим радиоспециалистам применять их для проверки многих самолетных и наземных антенн. Рассмотренный в этой лабораторной работе метод измерения входного сопротивления является универсальным и может быть использован в широком диапазоне частот. Студентам необходимо обратить внимание на погрешности метода и на способы повышения точности измерения.
Цель работы: 1. Изучение свойств логопериодических антенн. 2. Овладение методикой измерения входного сопротивления антенны с помощью измерительной линии. 3. Экспериментальное исследование зависимости входного сопротивления и диаграммы направленности от частоты.
Краткие теоретические сведения В ряде случаев требуется, чтобы антенна в широком диапазоне частот (о коэффициентом перекрытия диапазона Наиболее простой конструкцией обладает плоская ЛПА, представляющая собой линейную решетку симметричных вибраторов монотонно изменяющейся длины (рис.1). Вибраторы возбуждаются двухпроводным фидером. Линии, соединяющие концы вибратора, образуют угол полотна антенны Как видно из рис.1, логопериодическая структура удовлетворяет условию
Диаметр вибраторов
Расположение вибраторов в полотне антенны должно удовлетворять еще
Рис. 1
одному условию логопериодичности
Условие (2) не является критичным, поэтому даже при его нарушении антенна сохраняет частотную независимость. В связи с этим вибраторы могут выполняться с одинаковым поперечным сечением. Условия (I) и (3) должны удовлетворяться строго. Только при этом сохраняются основные свойства антенны. Пусть к точкам Вибраторы, длина которых близка или равна половине длины волны, имеют небольшое входное сопротивление с преобладанием активной составляющей. Токи в этих вибраторах будут значительны и интенсивность излучаемых электромагнитных волн по сравнению с интенсивностью волн, излучаемых остальными вибраторами, очень высокая. Интенсивно излучающие вибраторы образуют активную зону ЛПА. Вибраторы, длина которых больше активной зоны, слабо излучают, так как после активной зоны мощность электромагнитной волны в фидере резко падает. Это обусловлено тем, что в активной зоне почти вся мощность волны, подводимой фидером, расходуется на излучение. Для иллюстрации принципа действия ЛПА примем, что для некоторой длины волны активную зону образуют вибраторы
Значение Четвертый вибратор короче третьего, поэтому его входное сопротивление носит емкостной характер. В связи с этим ток в вибраторе будет сдвинут по фазе относительно тока в фидере на угол
Опережение по фазе на угол, превышающий 180°, можно рассматривать, как запаздывание по фазе на угол, меньший 180°. Таким образом, четвертый и третий вибраторы можно рассматривать как директор и антенну. Пространственные связи между вторым, третьим и четвертым вибраторами в еще большей степени способствуют созданию условий, существующих в директорной антенне, которая состоит из директора, излучателя и рефлектора. Следовательно, активная зона ЛПА на одной из собственных длин волн Направление главного максимума излучения совпадает с продольной осью антенны. Так как в формировании диаграммы направленности (ДН) принимает участие небольшое количество вибраторов (три-пять), то антенна будет слабонаправленной (главный лепесток направлен в сторону точки питания). Примерная ДН логопериодической антенны изображена на рис.2. В плоскости Е диаграмма направленности уже, чем в плоскости Н, так как в плоскости Е на формирование ДН сказываются направленные свойства отдельных излучателей. В плоскости Н вибраторы ненаправленные, поэтому результирующая ДН ЛIIA несколько шире. Увеличение параметра Ширина ДН зависит также и от угла
Рис.2 Рис.3
Максимальная длина волны определяется самым длинным вибратором
Резонансная длина волны определяется длиной вибратора антенны. Так для S -го вибратора резонансная длина волны равна
Из выражения (I) следует, что
Подставляя последнее соотношение в выражение (3), находим
Заменяя длину вибратора собственной длиной волны, получаем
Это выражение позволяет найти значение резонансной длины волны S-го вибратора по известному параметру
где На резонансных длинах волн параметры антенны определяются как параметры активной зоны, в середине которой один вибратор возбуждается на собственной длине волны. Так, в случае активной зоны, состоящей из трех вибраторов, ДН антенны и ее параметры на резонансных длинах волн будут близки к ДН и параметрам антенны типа волновой канал, содержащей рефлектор, активный вибратор и один директор. Так как относительная длина вибраторов активной зоны неизменна, то и параметры антенны для всех резонансных длин волн повторяются. При питании ЛПA токами, длины волн которых находятся в промежутках между резонансными длинами Логарифмируя выражение (4), имеем
Следовательно, на логарифмической шкале резонансные длины волн повторяются через одинаковые интервалы, равные В рабочей полосе длин волн входное сопротивление ЛПА мало меняется и при соответствующем выборе волнового сопротивления фидера в десятикратном диапазоне волн коэффициент бегущей волны не падает ниже 0,6...О,7. Участок распределительного фидера от вершины антенны до начала активной зоны работает как линия передачи. Короткие вибраторы, расположенные перед активной зоной, эквивалентны сосредоточенным емкостям, которые подключены через определенные интервалы к распределительной линии. В связи с этим, волновое сопротивление линии снижается до значений порядка 100 Ом, что обеспечивает хорошее согласование распределительной линии с активной зоной. Так как вся подводимая мощность в активной зоне расходуется на излучение, то в распределительном фидере отраженная волна очень мала и от вершины антенны до активной зоны фидер практически работает в режиме бегущей волны. Вибраторы, длина которых больше активной зоны, слабо отражают волны тока, так как после активной зоны мощность волны тока очень маленькая. Входное сопротивление ЛПА зависит от волнового сопротивления распределительного фидера без подключенных вибраторов
a
б
Рис.4
Изображенная на рис.1 ЛІІА является плоской. Все ее вибраторы неводятся в одной плоскости. Антенна такой конструкции обладает более широкой ДН в плоскости Н, чем в плоскости Е (см.рис.2). Плоскость Е поля излучения ЛПА определяется двумя прямыми: осью антенны 00'и осью вибраторов. Положение плоскости Н также определяется двумя прямыми, осью антенны и перпендикуляром к оси вибратора.
а
б в Рис.5 Сузить ДН в плоскости Н можно путем перехода к пространственной линейной, (рис.5,а), трапецеидальной (рис.5;б) или треугольной (рис.5,в) логопериодической антенне. В этом случае провода распределительного фидера располагаются под углом Теоретически рассчитать ДН антенны сложно, так как необходимо найти амплитуды и фазы токов в вибраторах, а затем поле излучения найти как сумму полей отдельных вибраторов. Токи в вибраторах зависят от напряжения между проводами распределительной линии и пространственной связи между вибраторами. Для их вычисления составляется система линейных уравнений, количество которых превышает количество вибраторов, учитываемых при расчете. Такая система решается с помощью ЭВМ. Логопериодические антенны используются как облучатели зеркальных и линзовых антенн в качестве элементов антенных решеток И слабонаправленных сверхширокодиапазонных УКВ антенн, как антенны связных радиоэлектронных систем KB диапазона и даже в диапазоне средних волн для радиовещания. В данной работе исследуют зависимость входного сопротивления логопериодической антенны от частоты, снимают диаграмму направленности и зависимость ширины ее главного лепестка от частоты. Весь объем этих исследований может быть выполнен на установке, блок-схема которой изображена на рис.6
Рис.6
Для исследования взята антенна Аи , выполненная из совмещенных ( Исследуемую антенну устанавливают на штативе, снабженном поворотным механизмом со шкалой. При измерении входного сопротивления ЛПА следует обратить внимание на расположение антенны Аи, чтобы свести к минимуму влияние установок и антенн, находящихся в лаборатории. Для снятия ДН в вертикальной плоскости, ЛПА разворачивают так, чтобы плоскость антенны заняла вертикальное положение. Входное сопротивление антенны измеряется с помощью измерительной линии. Измерительная линия представляет собой отрезок линии передачи с индикаторным устройством, позволяющим снять распределение напряжения вдоль линии. Впервые метод измерения полных сопротивлений с помощью измерительных линий был предложи В.В.Татариневым в 1931 г. для измерения входного сопротивления коротковолновых антенн. Из теории линий передачи известно, что комплексные амплитуды поперечных компонент напряженностей электрического и магнитного полей Е и Н в линии без потерь могут быть представлены в виде
и
где Для различных типов волн существует следующая связь между векторами напряженности электрического и магнитного полей: волны типа Е
волны типа Н
волны типа Т
где W- волновое сопротивление линии передачи; Отношение амплитуд напряженностей отраженной волны к падающей называют комплексным коэффициентом отражения
Если нагрузкой линии передачи длиной
где Выражения в квадратных скобках являются комплексными коэффициентами амплитуд напряженностей. Величина модуля коэффициента отражения не меняется вдоль идеальной линии, поэтому абсолютное значение амплитуды напряженности поля в функции координаты равно
Графики, иллюстрирующие распределение напряженностей полей вдоль линии при различных видах нагрузки, изображены на рис.7. Очевидно, что это распределение можно проследить при помощи зонда электрического, либо магнитного типа.
Рис.7
Как следует из выражений (5) и (6), коэффициент стоячей волны
Коэффициент бегущей волны
Комплексное сопротивление в произвольном сечении линии передачи может быть вычислено как
Если x=0, то последняя формула определяет комплексное сопротивление в конце линии, т.е. сопротивление нагрузки Используя выражения (5) и (6), получим
Выражение (8) можно преобразовать к виду
Следовательно, для измерения величины нагрузки необходимо знать комплексный коэффициент отражения. Модуль коэффициента отражения находят по величине коэффициента бегущей волны или коэффициента стоячей волны. Для определения фазы коэффициента отражения обратимся к выражению (5). Из уравнения видно, что минимальная интенсивность поля в линии передачи будет при условии, если
Отсюда
где p=0,1,2… Положение первого минимума от нагрузки соответствует координате
Положение максимумов вдоль линии находим из равенства
откуда
Расстояние от нагрузки до первого максимума определяем как
Таким образом, измерив коэффициент бегущей волны и расстояние от нагрузки до первого минимума (или максимума) напряженности поля в фидере, можно рассчитать полное сопротивление нагрузки. Если в выражении (7) начало отсчета координат отнести к первому минимуму и принять, что
В полученном выражении комплексное сопротивление в линии передачи в сечении с координатой X полностью определяется модулем коэффициента отражения и расстоянием сечения до первого минимума от конца. Выражение (10) служит для построения диаграммы полных сопротивлений в полярной системе координат. Радиальной координатой диаграммы является модуль коэффициента отражения, а угловой - фаза коэффициента отражения. Так как модуль коэффициента отражения однозначно определяется величиной Диаграмму помещают в круге с радиусом, равным единице, потому что модуль коэффициента отражения изменяется от 0 до 1. В соответствии с выражением (10) на диаграмме наносят семейства кривых
Круговая диаграмма полных сопротивлений изображена на рис.8. Вертикальная ось ее отградуирована в значениях относительной величины активного сопротивления та ; в верхней половине деления шкалы соответствуют значениям коэффициента бегущей волны, в нижней- коэффициенту стоячей волны. Диаграмма симметрична относительно вертикальной оси. Справа от вертикальной оси находится область положительных реактивных сопротивлений, слева- область отрицательных реактивных сопротивлений.
Рис.8
При измерении входного сопротивления антенны с помощью измерительной линии определяем коэффициент бегущей волны на верхней половине вертикальной оси диаграммы отмечаем точку, соответствующую измеренному значению поворачиваем прямую, проходящую через центр диаграммы от вертикальной оси по направлению "к нагрузке" на угол, соответствующий отношению по шкалам импеданса отсчитываем значения умножаем найденное значение импеданса на волновое сопротивление измерительной линии и получаем полное входное сопротивление антенны. Пример. Результаты измерения равны:
Схема измерительной линии изображена на рис.9. Устройство
Рис.9
состоит из фидера Ф, индикаторной головки И, зонда З, шкалы для отсчета положения индикаторной головки Ш. К выходу измерительной линии подключено сопротивление нагрузки Фидерами измерительных линий чаще всего являются коаксиальные линии и волноводы. В фидере прорезают неизлучающую щель параллельно оси для погружения зонда индикаторной головки, что позволяет снять распределение напряженности поля при передвижении индикаторной головки вдоль линии. Некоторые измерительные линии снабжаются электродвигателями для автоматического передвижения индикаторных головок. Индикаторная головка состоит из зонда для связи цепи детектора с электромагнитным полем внутри фидера, колебательного контура, который увеличивает чувствительность измерительного устройства, диода для детектирования высокочастотных токов и гальванометра. Определение полного сопротивления нагрузки связано с измерением распределения электрического поля вдоль измерительной линии и с расчетом Примерные результаты измерения приведены на рис.10. По оси абсцисс отложены координаты положения индикаторной головки Х , по оси ординат - показания
При квадратичной характеристике детектора
Рис.10
Для определения координаты При большом рассогласовании (
Расстояние d и величину
Рис.11
При квадратичной характеристике детектора формула (13) принимает вид
Если показания прибора в узле малы, то расчет коэффициента бегущей волны по формулам (13) и (14) приводит к большим погрешностям. В этом случае пользуются выражением
где При необходимости получить результат с большой точностью расчет повторяют по другим значениям точек кривой. Для ориентировочных расчетов выражение (14) может быть упрощено. Приняв
Расстояние d соответствует показанию прибора Вольт-амперные характеристики полупроводниковых диодов меняются со временем и у различных экземпляров диодов существенно отличаются друг от друга. Поэтому при каждой смене диодов, а также время от времени необходимо производить градуировку детектора. При этом используется то обстоятельство, что вдоль короткозамкнутой линии без потерь амплитуда напряженности поля распределяется по синусоидальному закону.
Рис.12 Рис.13
В процессе градуировки детектора выход измерительной линии закорачивают и снимают распределение напряженности поля. Результаты измерений
где Отсчет координаты Х производят от узла напряженности. Так как для фиксированных значений координаты Х показания прибора соответствуют относительной напряженности поля Y, то можно построить градуировочную кривую
Для точных измерений следует пользоваться градуировочной кривой. Во многих случаях можно аппроксимировать градуировочную кривую степенной функцией
где A- постоянный коэффициент; E- напряженность поля в линии; n- некоторое постоянное число. Отнесем начало отсчета к пучности напряженности поля. Тогда d соответствии с выражением (15) можно записать
Определим ширину кривой a на уровне
Кристаллические детекторы, работающие в области малых напряжений, имеют характеристику, близкую к квадратичной ( Выражение для полного сопротивления (10) можно преобразовать к виду
При измерении входного сопротивления антенны
и
Погрешность определения сопротивления может быть вычислена как полный дифференциал логарифма функции (17)
Относительная ошибка измерения активной составляющей входного сопротивления антенны равна
где После некоторых преобразований выражение упрощается
где для удобства записи обозначено
Аналогично выглядит выражение для относительной ошибки измерения реактивной составляющей входного сопротивления
Из анализа выражений (18) и (19) следует, что погрешность в определении координаты положения минимума Современные измерительные линии позволяют в целом измерять полные сопротивления о погрешностями порядка 5...10%.
Задание 1. Изучить измерительную аппаратуру и правила ее эксплуатаций. 2. Ознакомиться с методикой измерения входного сопротивления с помощью измерительной линии и измерить полное входное сопротивление ЛПА в заданных точках диапазона частот. 3. Ознакомиться с методикой снятия ДН, рассчитать минимально допустимое расстояние между антеннами и снять диаграммы направленности ЛПА в горизонтальной и вертикальной плоскостях. 4. Оценить погрешности измерения входного сопротивления и погрешности при снятии ДН. 5. По результатам измерений определить для заданного типа фидера
Поиск по сайту: |
 ) сохранила неизменными входное сопротивление и диаграмму направленности (ДН) Этому требованию удовлетворяют так называемые частотно-независимые антенны, коэффициент перекрытия диапазона которых достигает 10 и больше. К частотно-независимым антеннам относится антенна с логарифмической периодической структурой или логопериодическая антенна (ЛПА).
) сохранила неизменными входное сопротивление и диаграмму направленности (ДН) Этому требованию удовлетворяют так называемые частотно-независимые антенны, коэффициент перекрытия диапазона которых достигает 10 и больше. К частотно-независимым антеннам относится антенна с логарифмической периодической структурой или логопериодическая антенна (ЛПА).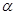 .
. . (1)
. (1)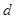 также должен удовлетворять условию логопериодичности
также должен удовлетворять условию логопериодичности . (2)
. (2)
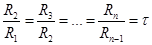 . (3)
. (3) подведено питание антенны. Электромагнитная волна будит распространяться по двухпроводной линии в сторону вибраторов возрастающей длины. Вибраторы, у которых размер
подведено питание антенны. Электромагнитная волна будит распространяться по двухпроводной линии в сторону вибраторов возрастающей длины. Вибраторы, у которых размер  значительно меньше половины длины волны, будут обладать высоким входным сопротивлением емкостного характера. Вследствие этого токи в вибраторах будут ничтожно малы и их поле излучения будет незначительным.
значительно меньше половины длины волны, будут обладать высоким входным сопротивлением емкостного характера. Вследствие этого токи в вибраторах будут ничтожно малы и их поле излучения будет незначительным. ,
, 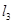 и
и  (рис.1) и что
(рис.1) и что  . Следовательно, третий вибратор возбуждается на собственной длине волны и его сопротивление чисто активное. Второй вибратор длиннее третьего, поэтому его входное сопротивление носит индуктивный характер. Из-за этого ток в вибраторе будет сдвинут по фазе относительно тока в фидере на некоторый угол
. Следовательно, третий вибратор возбуждается на собственной длине волны и его сопротивление чисто активное. Второй вибратор длиннее третьего, поэтому его входное сопротивление носит индуктивный характер. Из-за этого ток в вибраторе будет сдвинут по фазе относительно тока в фидере на некоторый угол  . Кроме того, волна тока проходит по распределительной линии к зажимам второго вибратора дополнительный путь, равный расстоянию между третьим и вторым вибраторами
. Кроме того, волна тока проходит по распределительной линии к зажимам второго вибратора дополнительный путь, равный расстоянию между третьим и вторым вибраторами 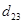 . Набег фазы волны при атом составит величину
. Набег фазы волны при атом составит величину 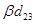 , где
, где  - коэффициент фазы волны и
- коэффициент фазы волны и  - длина волны в распределительной линии. Плечи второго вибратора по сравнению с плечами третьего вибратора присоединены к, взаимно противоположным проводам фидера, что обеспечивает фазовый сдвиг между токами второго и третьего вибраторов, равный
- длина волны в распределительной линии. Плечи второго вибратора по сравнению с плечами третьего вибратора присоединены к, взаимно противоположным проводам фидера, что обеспечивает фазовый сдвиг между токами второго и третьего вибраторов, равный  . Таким образом, ток второго вибратора будет запаздывать по фазе относительно тока третьего вибратора на угол
. Таким образом, ток второго вибратора будет запаздывать по фазе относительно тока третьего вибратора на угол .
. превосходит 180°, поэтому можно считать, что ток второго вибратора опережает ток третьего вибратора на угол, меньший 180°. Такой фазовый сдвиг характерен для системы, состоящей из антенны и рефлектора, причем роль рефлектора играет второй вибратор.
превосходит 180°, поэтому можно считать, что ток второго вибратора опережает ток третьего вибратора на угол, меньший 180°. Такой фазовый сдвиг характерен для системы, состоящей из антенны и рефлектора, причем роль рефлектора играет второй вибратор. . Путь тока от генератора до четвертого вибратора короче пути тока от генератора до третьего вибратора на отрезок распределительного фидера
. Путь тока от генератора до четвертого вибратора короче пути тока от генератора до третьего вибратора на отрезок распределительного фидера  . Набег фазы волны тока на этом отрезке составляет величину
. Набег фазы волны тока на этом отрезке составляет величину  . С учетом того, что плечи третьего и четвертого вибраторов присоединены к взаимно противоположным проводам фидера, ток четвертого вибратора будет опережать по фазе ток третьего вибратора на угол
. С учетом того, что плечи третьего и четвертого вибраторов присоединены к взаимно противоположным проводам фидера, ток четвертого вибратора будет опережать по фазе ток третьего вибратора на угол .
. представляет собой директорную антенну (волновой канал), состоящую из трех вибраторов. При изменении длины волны активная зона смешается вдоль ЛПА. Например, при увеличении длины волны будут интенсивно излучать первый, второй и третий вибраторы, при уменьшении - третий, четвертый и пятый вибраторы.
представляет собой директорную антенну (волновой канал), состоящую из трех вибраторов. При изменении длины волны активная зона смешается вдоль ЛПА. Например, при увеличении длины волны будут интенсивно излучать первый, второй и третий вибраторы, при уменьшении - третий, четвертый и пятый вибраторы. при неизменном угле полотна антенны
при неизменном угле полотна антенны 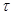 , тем меньше отличаются по длине соседние вибраторы, и тем меньше затухает ток в вибраторах по море удаления их от резонансного вибратора). Однако увеличение
, тем меньше отличаются по длине соседние вибраторы, и тем меньше затухает ток в вибраторах по море удаления их от резонансного вибратора). Однако увеличение 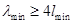 .
.
 . Практически антенну выполняют так, чтобы после вибратора, длина которого равна
. Практически антенну выполняют так, чтобы после вибратора, длина которого равна  , имелись еще один или два вибратора большей длины и до вибратора с длиной
, имелись еще один или два вибратора большей длины и до вибратора с длиной  располагались один- два вибратора более коротких. Таким образом, длина ЛПА из формулы (1) определяется как
располагались один- два вибратора более коротких. Таким образом, длина ЛПА из формулы (1) определяется как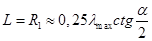 .
. или
или  .
. или
или 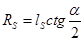 .
. .
.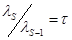
 , (4)
, (4) - собственная длина волны первого вибратора.
- собственная длина волны первого вибратора.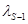 и
и  , ДН и параметры антенны несколько изменяются. При конструировании антенны ее постоянные
, ДН и параметры антенны несколько изменяются. При конструировании антенны ее постоянные 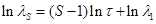 .
. . Это обстоятельство и определило название антенны.
. Это обстоятельство и определило название антенны. (рис.4,а) и от параметров
(рис.4,а) и от параметров 

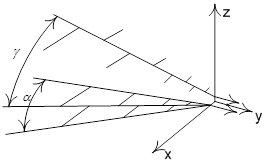

 друг к другу. Вибраторы, присоединенные к разным проводам распределительного фидера, размещаются в разных плоскостях. При этом ДН в плоскости Е сохраняет свою ширину, а в плоскости Н ДН сужается и при некотором угле
друг к другу. Вибраторы, присоединенные к разным проводам распределительного фидера, размещаются в разных плоскостях. При этом ДН в плоскости Е сохраняет свою ширину, а в плоскости Н ДН сужается и при некотором угле 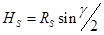 ). Диапазонные свойства пространственной ЛПА такие же, как и у плоской антенны.
). Диапазонные свойства пространственной ЛПА такие же, как и у плоской антенны.
 ) периодических структур с треугольными вибраторами. Антенна Аи через измерительную линию (ИЛ) и аттенюатор (Ат) присоединяется к генератору высокой частоты (ГВЧ). Вспомогательная антенна Ав используется для снятия диаграмм направленности индикатором поля (ИП).
) периодических структур с треугольными вибраторами. Антенна Аи через измерительную линию (ИЛ) и аттенюатор (Ат) присоединяется к генератору высокой частоты (ГВЧ). Вспомогательная антенна Ав используется для снятия диаграмм направленности индикатором поля (ИП).

 ,
,  - амплитуды напряженностей падающей волны на конце фидера;
- амплитуды напряженностей падающей волны на конце фидера; 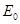 ,
,  - амплитуды напряженностей отраженной волны на конце фидера;
- амплитуды напряженностей отраженной волны на конце фидера;  - волновое число;
- волновое число;  - длина волны в линии; х- координата точки наблюдения, отсчитываемая от конца линии (от нагрузки).
- длина волны в линии; х- координата точки наблюдения, отсчитываемая от конца линии (от нагрузки). ;
; ;
; ,
,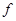 - частота колебаний электромагнитной волны;
- частота колебаний электромагнитной волны;  - критическая частота.
- критическая частота. .
. является элемент, характеризующийся коэффициентом отражения
является элемент, характеризующийся коэффициентом отражения  , то
, то (5)
(5) (б)
(б) .
. .
.
 определяется соотношением
определяется соотношением .
. .
.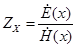
 .
. , (7)
, (7) . (8)
. (8) .
. .
. или
или 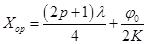 ,
, . (9)
. (9) ,
, . Координаты, характеризующие положение максимумов,
. Координаты, характеризующие положение максимумов,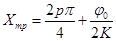 .
.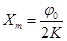 .
. , то, учитывая выражение (9), найдем
, то, учитывая выражение (9), найдем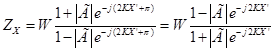 . (10)
. (10) или
или 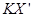 или же отношение
или же отношение  .
.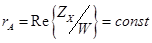 и
и 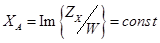
 .
.
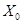 . Расчет полного сопротивления производим в следующем порядке:
. Расчет полного сопротивления производим в следующем порядке: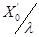 или
или  ;
; и
и  , соответствующие точке пересечения окружности радиуса, равного
, соответствующие точке пересечения окружности радиуса, равного  и
и 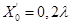 . На рис. 2 отмечена точка А (
. На рис. 2 отмечена точка А (  и
и  . Следовательно, полное сопротивление равно
. Следовательно, полное сопротивление равно Ом .
Ом .
 по известному распределению коэффициента бегущей волны
по известному распределению коэффициента бегущей волны  . (11)
. (11) . (12)
. (12)
 ) возникают трудности в измерении
) возникают трудности в измерении 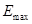 и
и  с помощью одношкального индикаторного прибора. Отклонение стрелки гальванометра при
с помощью одношкального индикаторного прибора. Отклонение стрелки гальванометра при 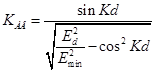 . (13)
. (13) находим из участка кривой распределения напряженности вдоль линии в области минимума (рис.2). Повышение точности определения коэффициента бегущей волны достигается расчетом
находим из участка кривой распределения напряженности вдоль линии в области минимума (рис.2). Повышение точности определения коэффициента бегущей волны достигается расчетом 
 . (14)
. (14) ,
, ,
, 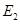 ,
,  ,
,  определяются в области минимума, как, показано на рис. 12.
определяются в области минимума, как, показано на рис. 12.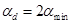 и учитывая, что
и учитывая, что  , из выражения (14) получим
, из выражения (14) получим .
.
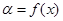 наносят на график (рис. 13, кривая а), где по оси абсцисс отложена координата положения индикаторной головки Х, а по оси ординат - показания прибора
наносят на график (рис. 13, кривая а), где по оси абсцисс отложена координата положения индикаторной головки Х, а по оси ординат - показания прибора  .
. ,
, - волновое число;
- волновое число;  - длина волны в линии;
- длина волны в линии;  - максимальное показание индикатора.
- максимальное показание индикатора.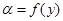 .
. , (І5)
, (І5)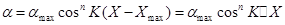 .
. графика, приведенного на рис.13. Тогда показатель степени можно найти из выражения
графика, приведенного на рис.13. Тогда показатель степени можно найти из выражения . (16)
. (16) ).
). . (17)
. (17) и
и  , поэтому
, поэтому
 .
. .
. ,
,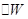 - абсолютная ошибка определения волнового сопротивления линии;
- абсолютная ошибка определения волнового сопротивления линии;  - абсолютная ошибка измерения;
- абсолютная ошибка измерения;  - абсолютная ошибка измерения расстояния от нагрузки до первого минимума.
- абсолютная ошибка измерения расстояния от нагрузки до первого минимума. ,
,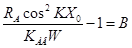 .
.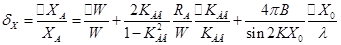 , (19)
, (19)