 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоретическое обоснование метода измерения теплопроводности в монотонном режимеСтр 1 из 2Следующая ⇒
Введение Цель работы заключается: · в закреплении лекционного материала по теоретическим основам метода монотонного режима для измерения коэффициента теплопроводности · в изучении принципиальной конструкции измерителя ИТ- · в приобретении навыков экспериментального определения
Элементы исследования Элементы исследования при проведении лабораторных работ включает: · получение экспериментальной зависимости · построение графической зависимости · проведение оценок погрешности результатов измерения и анализ полученных результатов. Теоретическое обоснование метода измерения теплопроводности в монотонном режиме Основные закономерности монотонного режима Рассмотрим неограниченную пластину образец 1 толщиной Распределение температуры в пластине 1 описывается одномерным нестационарным уравнением теплопроводности (1) и краевыми условиями (2)÷(4):
Рис. 1. Двухслойная система - металлическое ядро 2 и теплоизоляционная оболочка 1 при нагреве постоянным потоком: а – распределение
При достижении определенного времени от начала процесса нагрева
Для решения системы (5)÷(7) проинтегрируем дважды уравнение (5), получим
Используя граничные условия (6) и (7) найдем значения константы
Применяя формулу (10) к точке с координатой
получим
Из формулы (12) следует расчетные соотношения для определения теплового сопротивления образца
Где
Если между пластинами 1 и 2 имеет место неидеальный тепловой контакт и известна температура пластины 2, то в формуле (13) необходимо учитывать тепловое сопротивление контакта
Методика расчета теплового потока
Поиск по сайту: |
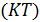 в практической работе о промышленным измерителем ИТ-
в практической работе о промышленным измерителем ИТ-  -400;
-400; образца, обработки результатов измерения и анализа полученных данных.
образца, обработки результатов измерения и анализа полученных данных. , подбор и определение эмпирической формулы этой зависимости на основе метода наименьших квадратов;
, подбор и определение эмпирической формулы этой зависимости на основе метода наименьших квадратов; на плохопроводящего материала, которая находится в идеальном тепловом контакте с металлической пластиной 2, имеющей толщину
на плохопроводящего материала, которая находится в идеальном тепловом контакте с металлической пластиной 2, имеющей толщину  (рис. 1, а). На лицевую грань пластины 1 действует постоянный тепловой потом плотности
(рис. 1, а). На лицевую грань пластины 1 действует постоянный тепловой потом плотности 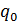 , тыльная сторона пластины 2адиабатизирована
, тыльная сторона пластины 2адиабатизирована 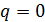 и температурное поле в ней остается практически равномерным на всех стадиях процесса.
и температурное поле в ней остается практически равномерным на всех стадиях процесса.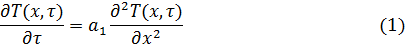


 ;б – зависимости
;б – зависимости 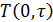 и
и  .
.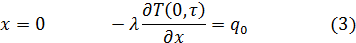
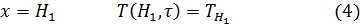
 , все слои системы повышают температуру с одинаковой постоянной скоростью
, все слои системы повышают температуру с одинаковой постоянной скоростью 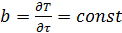 (квазистационарная стадия процесса) и температурное поле
(квазистационарная стадия процесса) и температурное поле 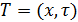 в пластине 1перестаетзависит от начальных условий (рис.1б). В этом случае вышеприведенная математическая постановка задачи для определения температурного поля в пластине упрощается и имеет вид:
в пластине 1перестаетзависит от начальных условий (рис.1б). В этом случае вышеприведенная математическая постановка задачи для определения температурного поля в пластине упрощается и имеет вид:
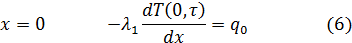


 :
: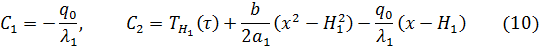
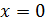 и заменяя скорость нагрева выражением из интегрального баланса
и заменяя скорость нагрева выражением из интегрального баланса

 и его теплопроводности соответственно:
и его теплопроводности соответственно: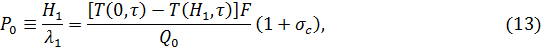


 - тепловой поток, поступающий в образец;
- тепловой поток, поступающий в образец;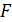 - площадь сечения пластины, м2;
- площадь сечения пластины, м2; - полная теплоемкость пластины 1;
- полная теплоемкость пластины 1;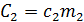 - полная теплоемкость пластины 2, Дж/К.
- полная теплоемкость пластины 2, Дж/К. и для расчета теплового сопротивления образца использовать выражение
и для расчета теплового сопротивления образца использовать выражение