 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Понятие площади, свойства площади. ⇐ ПредыдущаяСтр 2 из 2
Вычисление площади основывается на следующих основных свойствах площади:
За единицу измерения площади примем площадь элементарного квадрата со стороной r. Рассмотрим ограниченную фигуру G в прямоугольной декартовой системе координат, ее площадь обозначим S(G). Построим прямые, параллельные оси абсцисс и оси ординат на расстоянии r друг от друга. Эти прямые образуют сетку и разбивают плоскость xOy на элементарные квадраты. Обозначим
Если бесконечно уменьшать длину стороны элементарного квадрата r (делать сетку гуще), то получим множество значений площадей
Множество Фигуру G, у которой внешняя площадь равна внутренней, называют квадрируемой и число Равенство Площадью границы фигуры G называют предел последовательности значений площади Следует заметить, что понятие квадрируемости можно ввести и иначе, например, если рассматривать вписанные и описанные многоугольные фигуры (многоугольной фигурой называют фигуру, которую можно составить из конечного числа треугольников без общих внутренних точек). Фигура G называется квадрируемой, если для любого сколь угодно малого положительного числа В качестве примера можно привести круг с вписанными и описанными правильными К началу страницы Квадрируемые фигуры.
Сейчас выясним как же выглядят и как задаются квадрируемые фигуры. Другими словами, площадь каких фигур нам предстоит находить. Сразу скажем, что фигуры, с которыми мы обычно встречаемся в геометрии (круг, эллипс, квадрат и т.п.), являются квадрируемыми. Отметим, что любая квадрируемая фигура ограничена. То есть, мы не будем говорить о площади неограниченных фигур. Объединение и пересечение, а также разность квадрируемых фигур есть квадрируемая фигура. Сейчас перечислим виды квадрируемых фигур, с которыми мы будем наиболее часто встречаться при вычислении площадей.
Примеры вычисления площадей таких фигур Вы можете посмотреть в статье нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y).
Нахождению площадей таких квадрируемых фигур посвящена статья вычисление площади фигуры, ограниченной параметрически заданной кривой.
Можете ознакомиться с материалом статьи вычисление площади фигуры в полярных координатах. Подведем итог. Площадь – это единственная функция, определенная на классе квадрируемых фигур и обладающая свойствами положительности, аддитивности, инвариантности и нормированности.
Поиск по сайту: |
 – фигуру, состоящую из элементарных квадратов, полностью лежащих внутри G и не касающихся ее границы (красная заштрихованная область на рисунке), а
– фигуру, состоящую из элементарных квадратов, полностью лежащих внутри G и не касающихся ее границы (красная заштрихованная область на рисунке), а  - фигуру, состоящую из элементарных квадратов, которые имеют с границей G хотя бы одну общую точку (синяя заштрихованная область на рисунке), а
- фигуру, состоящую из элементарных квадратов, которые имеют с границей G хотя бы одну общую точку (синяя заштрихованная область на рисунке), а  - фигуру, являющуюся объединением
- фигуру, являющуюся объединением  и
и  , они равны количеству составляющих их элементарных квадратов.
, они равны количеству составляющих их элементарных квадратов.
 и
и 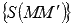 .
.
 , назовем ее внутренней площадью фигуры G. Множество
, назовем ее внутренней площадью фигуры G. Множество  , назовем ее внешней площадью фигуры G.
, назовем ее внешней площадью фигуры G. есть площадь этой фигуры.
есть площадь этой фигуры. при
при  . Для квадрируемой фигуры G площадь границы равна нулю.
. Для квадрируемой фигуры G площадь границы равна нулю. существуют такие входящая и объемлющая многоугольные фигуры P и Q, что
существуют такие входящая и объемлющая многоугольные фигуры P и Q, что 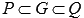 и
и  .
.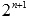 -угольниками, где n – натуральное число.
-угольниками, где n – натуральное число. , снизу кривой
, снизу кривой  , справа и слева прямыми x = 1 и x = 9. На втором рисунке в качестве границ области выступают линии
, справа и слева прямыми x = 1 и x = 9. На втором рисунке в качестве границ области выступают линии  .
. 
 . Функции
. Функции  и
и  непрерывны вместе со своими производными на некотором интервале
непрерывны вместе со своими производными на некотором интервале  и не имеют самопересечений, что равносильно условию
и не имеют самопересечений, что равносильно условию 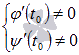 для любого
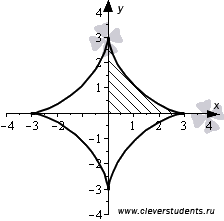
для любого  . В качестве примера можно привести фигуру, ограниченную осями координат и частю астроиды
. В качестве примера можно привести фигуру, ограниченную осями координат и частю астроиды  для
для  .
. 
 .
. 