 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод наименьших квадратов (МНК).
Пример. Экспериментальные данные о значениях переменных х и у приведены в таблице. В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Суть метода наименьших квадратов (МНК). Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b Таким образом, решение примера сводится к нахождению экстремума функции двух переменных. Вывод формул для нахождения коэффициентов. Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК). При данных а и b функция Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы Пришло время вспомнить про исходый пример. Решение. В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов. Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i . Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i . Значения последнего столбца таблицы – это суммы значений по строкам. Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы: Следовательно, y = 0.165x+2.184 - искомая аппроксимирующая прямая. Осталось выяснить какая из линий y = 0.165x+2.184 или
Поиск по сайту: |
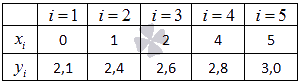

 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.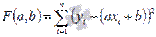 по переменным а и b, приравниваем эти производные к нулю.
по переменным а и b, приравниваем эти производные к нулю.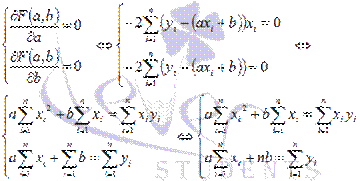

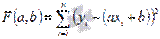 принимает наименьшее значение. Доказательство этого факта приведено ниже по тексту в конце страницы .
принимает наименьшее значение. Доказательство этого факта приведено ниже по тексту в конце страницы .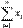 ,
, 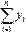 ,
, 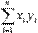 ,
, 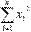 и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a.
и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a.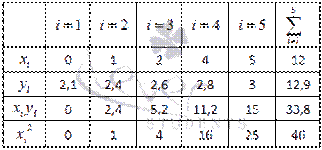

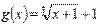 лучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов.
лучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов.