 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Частица в одномерной потенциальной яме. Квантование энергии.
Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
где l - ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).
Рис. 296 Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = l)непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
В пределах «ямы» (0 £ х £ l) уравнение Шредингера (220.1) сведется к уравнению
Общее решение дифференциального уравнения (220.3): Y(x) = Asin kx + Bcos kx. Так как по (220.2) y(x) = 0, то B = 0. Тогда
Условие (220.2) Y(l) = Asin kl выполняется только при kl = np, где n - целые числа, т. е. необходимо, чтобы
Из выражений (220.4) и (220.6) следует, что т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях , зависящих от целого числа n. Следовательно, энергия Enчастицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется. Квантованные значения энергии Enназываются уровнями энергии, а число л, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне En, или, как говорят, частица находится в квантовом состоянии n. Подставив в (220.5) значение k из (220.6), найдем собственные функции:
Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде
В результате интегрирования получим
а собственные функции будут иметь вид
Графики собственных функций (220.8), соответствующие уровням энергии (220.7) при n = 1, 2, 3, приведены на рис. 297,а.На рис. 297,б изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |Yn(x)|2 = Yn(x) Y*n(x) для n = 1, 2 и 3.
Рис. 297 Из рисунка следует, что, например, в квантовом состоянии с n = 2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны. Из выражения (220.7) вытекает, что энергетический интервал между двумя сосед ними уровнями равен
Например, для электрона при размерах ямы l = 10-1 м (свободные электроны в металле) DEn » 10-35 n Дж »10-16 n эВ, т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными (l = 10-10 м), то для электрона DEn » 10-17 n Дж »102 n эВ, т. е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает. Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная p2ℏ2/(2ml2). Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Аде частицы в «яме» шириной l равна Dx = l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса Dр » h/l. Такому разбросу значений импульса соответствует кинетическая энергия Emin »(Dp)2/(2m) = h2/(2ml2). Все остальные уровни (n > 1) имеют энергию, превышающую это минимальное значение. Из формул (220.9) и (220.7) следует, что при больших квантовых числах (n >> 1) DEn/En » 2/n << 1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов - дискретность - сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики. Туннельный эффект. Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 298, а) для одномерного (по оси х)движения частицы. Для потенциального барьера прямоугольной формы высоты Uи ширины l можем записать
(для области 2), (для области 3). При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е > U),либо отразится от него (при Е < U)и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при E > U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E < Uимеется также отличная от нуля вероятность, что частица окажется в области х >l,т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микро частицы при условиях данной задачи.
Рис. 298 Уравнение Шредингера (217.5) для стационарных состояний для каждой из выделенных на рис. 298, а области имеет вид Общие решения этих дифференциальных уравнений:
(для области 2); (для области 3). (221.3) В частности, для области 1полная волновая функция, согласно (217.4), будет иметь вид В этом выражении первый член представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (соответствует частице, движущейся в сторону барьера), а второй - волну, распространяющуюся в противоположном направлении, т. е. отраженную от барьера (соответствует частице, движущейся от барьера налево). Решение (221.3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент В3 в формуле (221.3) следует принять равным нулю. В области 2 решение зависит от соотношений Е > U или Е < U. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера, поскольку при Е < Uзаконы классической физики однозначно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (221.1), q = ib - мнимое число, где
Учитывая значение qи B3=0, получим решения уравнения Шредингера для трех областей в следующем виде:
В области 2 функция (221.5) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Можно показать, что для частного случая высокого и широкого барьера, когда bl >>1, B2 » 0 . Качественный характер функций y1(x), y2(x), y3(x) иллюстрируется на рис. 298, б, откуда следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины. Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер. С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е < Uневозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Dр на отрезке Dx = l составляет Dр > h/l. Связанная с. этим разбросом в значениях импульса кинетическая энергия (Dр)2/(2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.
Поиск по сайту: |
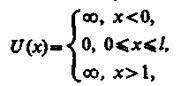

 (220.1)
(220.1)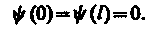 (220.2)
(220.2)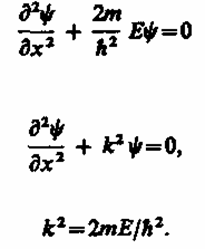

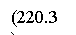
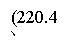 где
где (220.5)
(220.5) (220.6)
(220.6)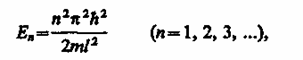 (220.7)
(220.7)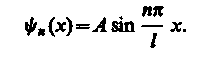


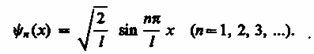 (220.8)
(220.8)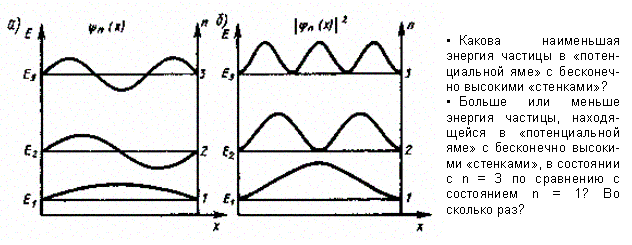
 (220.9)
(220.9) (для области 1),
(для области 1),
 (221.1)
(221.1) (для области 1); (221.2)
(для области 1); (221.2)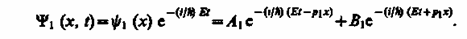 (221.4)
(221.4)
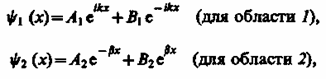
 (для области 3). (221.5)
(для области 3). (221.5)