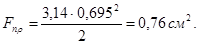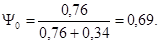|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
экспериментов и их результаты
ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ
2.1. Выбор интервалов варьирования исследуемых факторов
Интервал варьирования тока дуги Таблица 5 Условия проведения полного трехфакторного эксперимента
Прежде, чем приступить к исследованиям по плану, проведем оценку воспроизводимости опытов. Для этого выполним три серии параллельных опытов в исследуемой области. В каждой сери проведем по два параллельных опыта.
Таблица 6. Условия проведения опытов и результаты измерений
Расчеты Рассчитываем критерий Кохрена для опытов:
Критическое значение критерия Кохрена для числа степеней свободы Поскольку Для проведения трехфакторного эксперимента приведем таблицу его плана [8].
Таблица 7 Полный трехфакторный эксперимент
Для того чтобы избежать ошибок при проведении эксперимента, табл.7 заполним конкретными значениями параметров.
Таблица 8 Значения параметров при проведении численных экспериментов и их результаты
На основании результатов полного 3-факторного эксперимента вычисляем коэффициенты регрессии по формулам [8].
Коэффициенты при парных произведениях факторов:
Свободный член уравнения регрессии Рассчитываем оценку дисперсии, с которой определяются коэффициенты уравнения регрессии. Оценка дисперсии воспроизводимости
С оценкой дисперсии
Проверим значимость коэффициентов регрессии. Табличное значение критерия Стьюдента После исключения незначимых коэффициентов уравнения регрессии принимает вид Проверим адекватность полученного уравнения регрессии. Найдем расчетное значение функции отклика для первого опыта, подставим в уравнение регрессии значение кодированных переменных:
Расчетные значения функции отклика для остальных опытов приведены в табл.9.
Таблица 9
Рассчитаем оценку дисперсии адекватности:
Число степеней свободы, связанное с оценкой дисперсии адекватности, Вычислим расчетное значение критерия Фишера Получим уравнение регрессии для физических переменных. Кодированные переменные связаны с физическими соотношениями
Подставив эти выражения в уравнение регрессии и приведя затем подобные члены, получим уравнения регрессии в физических переменных:
Из уравнения регрессии следует, что с увеличением тока дуги глубина проплавления возрастает. Влияние скорости наплавки противоположно. Уравнение регрессии позволяет найти в данной области режимов значения факторов, обеспечивающие требуемую глубину проплавления.
2.2. Определение химического состава металла шва
Расчет химического состава будем вести в предложении, что при наплавке не происходит выгорания химических элементов электродной проволоки и шва из-за воздействия температуры дуги и химических реакций. Скорость подачи электродной проволоки будем рассчитывать из функциональной зависимости Площадь поперечного сечения наплавленного металла
где Площадь проплавления основного металла, учитывая, что она представляет собой полукруг радиусом
Подставив
Доля участия основного металла в металле шва
При отсутствии химических реакций в зоне сварки содержание любого элемента в металле шва
где Пользуясь формулами (1) – (6), можно решить ряд задач. Например, можно попытаться получить при заданной глубине проплавления Определим содержание в шве марганца при следующем режиме наплавки:
Площадь наплавки
Глубина проплавления:
Площадь проплавления:
Доля основного металла:
Содержание марганца в шве:
ВЫВОД: Варьируя параметры режима (ток, скорость наплавки, температуру подогрева) на математической модели, а, следовательно, и все свойства, зависящие от химического состава. Наиболее целесообразно такие расчеты выполнять с помощью специальной программы на ЭВМ.
Поиск по сайту: |
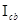 выберем в соответствии с интервалом в рекомендуемом режиме 280…400 А. Скорость наплавки также будем варьировать в пределах 15…25 м/час, температуру подогрева изделия выберем от +20°С до +220°С. Примем
выберем в соответствии с интервалом в рекомендуемом режиме 280…400 А. Скорость наплавки также будем варьировать в пределах 15…25 м/час, температуру подогрева изделия выберем от +20°С до +220°С. Примем 
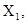 А
А
 см/с
см/с
 град
град








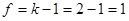 и трех серий опытов составляет 0,967.
и трех серий опытов составляет 0,967. то опыты воспроизводимы.
то опыты воспроизводимы. А
А
 см/с
см/с
 град
град
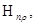 мм
мм





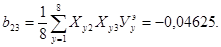

 из трех предварительных серий опытов:
из трех предварительных серий опытов:
 Тогда оценки дисперсии, с которой вычисляются коэффициенты регрессии,
Тогда оценки дисперсии, с которой вычисляются коэффициенты регрессии,
 4,30. Коэффициент значим, если выполняется условие
4,30. Коэффициент значим, если выполняется условие  Коэффициент
Коэффициент  не будет исключать из уравнения регрессии, т.к.
не будет исключать из уравнения регрессии, т.к. 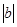 близко к
близко к 





 Критическое значение Фишера в данном случае равно 19,25. Следовательно, найденное нами уравнение регрессии адекватно описывает экспериментальные данные.
Критическое значение Фишера в данном случае равно 19,25. Следовательно, найденное нами уравнение регрессии адекватно описывает экспериментальные данные.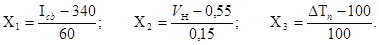
 (1)
(1) и условия. Что току
и условия. Что току 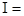 200А соответствует
200А соответствует  105 м/час, а току
105 м/час, а току  -45 ,
-45 ,  0,75 [7].
0,75 [7]. (2)
(2) – площадь поперечного сечения электродной проволоки.
– площадь поперечного сечения электродной проволоки.
 (3)
(3) из (1) в (3), получим зависимость
из (1) в (3), получим зависимость  от режимов наплавки:
от режимов наплавки: (4)
(4)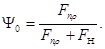 (5)
(5) может быть найдено по формуле
может быть найдено по формуле (6)
(6) – исходное содержание элемента в основном электродном металле.
– исходное содержание элемента в основном электродном металле. требуемый процент содержания, какого – либо элемента в шве.
требуемый процент содержания, какого – либо элемента в шве.