 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Интерпретация условий Куна — Таккера
Условия Куна—Таккера и задача Куна—Таккера Найти векторы
Прежде всего проиллюстрируем условия Куна — Таккера на примере. Пример 3 Минимизировать Решение. Записав данную задачу в виде задачи нелинейного программирования (0)-(2), получим
Уравнение (3), входящее в состав условий Куна—Таккера, принимает следующий вид: откуда
Неравенства (4) и уравнения (5) задачи Куна — Таккера в данном случае записываются в виде
Уравнения (5.16), известные как условие дополняющей нежесткости, принимают вид
Заметим, что на переменные Таким образом, этой задачи условия Куна—Танкера записываются в следующем виде:
Интерпретация условий Куна — Таккера Для того чтобы интерпретировать условия Куна — Таккера, рассмотрим задачу нелинейного программирования с ограничениями в виде равенств: минимизировать при ограничениях Запишем условия Куна—Таккера
Далее рассмотрим функцию Лагранжа для задачи нелинейного программирования с ограничениями в виде равенств
Для этой функции условия оптимальности первого порядка записываются в виде
Нетрудно видеть, что условия Куна-Таккера (8) и (9) совпадают с условиями оптимальности первого порядка для задачи Лагранжа. Рассмотрим задачу нелинейного программирования с ограничениями в виде неравенств: минимизировать при ограничениях Запишем условия Куна—Таккера
Соответствующая функция Лагранжа имеет вид
Условия оптимальности первого порядка записываются как
Заметим, что Если предположить, что Для того чтобы определить знак Теоремы Куна—Таккера В предыдущем разделе построены условия Куна—Таккера для задач условной оптимизации. С помощью метода множителей Лагранжа получено интуитивное представление о том, что условия Куна — Танкера тесно связаны с необходимыми условиями оптимальности. В данном разделе рассматриваются строгие формулировки необходимых и достаточных условий оптимальности решения задачи нелинейного программирования. Теорема 1. Необходимость условий Куна—Таккера Рассмотрим задачу нелинейного программирования (0)-(2). Пусть Условие, согласно которому 1. Все ограничения в виде равенств и неравенств содержат линейные функции. 2. Все ограничения в виде неравенств содержат вогнутые функции, все ограничения-равенства — линейные функции, а также существует, по крайней мере, одна допустимая точка х, которая расположена во внутренней части области, определяемой ограничениями-неравенствами. Другими словами, существует такая точка х, что Если условие линейной независимости в точке оптимума не выполняется, то задача Куна—Таккера может не иметь решения. Пример 4 Минимизировать при ограничениях Решение. На рис.1 изображена область допустимых решений сформулированной выше нелинейной задачи. Ясно, что оптимальное решение этой задачи есть
Рис.1 Допустимая область в задаче 4 Так как
Запишем условия Куна—Таккера и проверим, выполняются ли они в точке (1, 0). Условия (3), (6) и (7) принимают следующий вид;
При
Нетрудно проверить, что точка Теорема о необходимости условий Куна—Таккера позволяет идентифицировать неоптимальные точки. Другими словами, теорему 1 можно использовать для доказательства того, что заданная допустимая точка, удовлетворяющая условию линейной независимости, не является оптимальной, если она не удовлетворяет условиям Куна—Таккера. С другой стороны, если в этой точке условия Куна—Таккера выполняются, то нет гарантии, что найдено оптимальное решение нелинейной задачи. В качестве примера рассмотрим следующую задачу нелинейного программирования. Следующая теорема устанавливает условия, при выполнении которых точка Куна—Таккера автоматически соответствует оптимальному решению задачи нелинейного программирования. Теорема.2 Достаточность условий Куна—Таккера Рассмотрим задачу нелинейного программирования (0) — (2). Пусть целевая функция Если условия теоремы 2 выполняются, то нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение
Так как матрица чтобы показать, что функция
Поскольку матрица
Точка
Положив Замечания 1.Для встречающихся на практике задач условие линейной независимости, как правило, выполняется. Если в задаче все функции дифференцируемы, то точку Куна—Таккера следует рассматривать как возможную точку оптимума. Таким образом, многие из методов нелинейного программирования сходятся к точке Куна—Таккера. (Здесь уместно провести аналогию со случаем безусловной оптимизации, когда соответствующие алгоритмы позволяют определить стационарную точку.) 2. Если условия теоремы 2 выполнены, точка Куна—Таккера в то же время оказывается точкой глобального минимума. К сожалению, проверка достаточных условий весьма затруднительна, и, кроме того, прикладные задачи часто не обладают требуемыми свойствами. Следует отметить, что наличие хотя бы одного нелинейного ограничения в виде равенства приводит к нарушению предположений теоремы 2. 3.Достаточные условия, установленные теоремой 2, можно обобщить на случай задач с невыпуклыми функциями, входящими в ограничения в виде неравенств, невыпуклыми целевыми функциями и нелинейными ограничениями-равенствами. При этом используются такие обобщения выпуклых функций, как квазивыпуклые и псевдовыпуклые функции.
Поиск по сайту: |
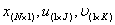 ,удовлетворяющие следующим условиям
,удовлетворяющие следующим условиям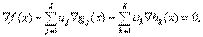 (3)
(3) (4)
(4)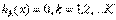 (5)
(5)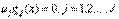 (6)
(6)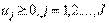 (7)
(7)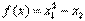 при ограничениях
при ограничениях 
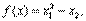
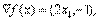
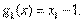
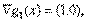
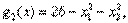
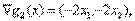
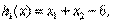
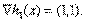
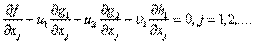
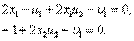
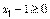
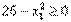

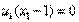
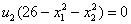
 и
и 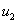 накладывается требование неотрицательности, тогда как ограничение на знак
накладывается требование неотрицательности, тогда как ограничение на знак 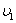 отсутствует.
отсутствует.
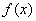
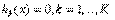
 (8)
(8) (9)
(9)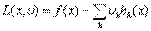
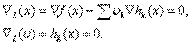
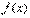





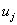 - множитель Лагранжа, соответствующий ограничению
- множитель Лагранжа, соответствующий ограничению  . Раньше было показано, что
. Раньше было показано, что 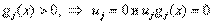 С другой стороны, если
С другой стороны, если 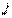 -е ограничение активное (т. е.
-е ограничение активное (т. е. 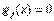 ), то соответствующая неявная цена
), то соответствующая неявная цена 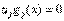 , так как
, так как 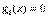 . Таким образом,
. Таким образом,  для всех значений
для всех значений 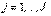 .
.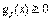 ), следует увеличить правую часть ограничения от 0 до 1. Ясно, что при этом область допустимых решений сужается, поскольку любое решение, удовлетворяющее ограничению
), следует увеличить правую часть ограничения от 0 до 1. Ясно, что при этом область допустимых решений сужается, поскольку любое решение, удовлетворяющее ограничению 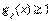 , автоматически удовлетворяет неравенству
, автоматически удовлетворяет неравенству 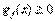 . Следовательно, размеры допустимой области уменьшаются, и минимальное значение
. Следовательно, размеры допустимой области уменьшаются, и минимальное значение 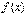 улучшить невозможно (так как вообще оно может только возрастать). Другими словами, неявная цена
улучшить невозможно (так как вообще оно может только возрастать). Другими словами, неявная цена 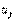 , ассоциированная с
, ассоциированная с 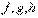 - дифференцируемые функции, а х* — допустимое решение данной задачи. Положим
- дифференцируемые функции, а х* — допустимое решение данной задачи. Положим 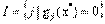 . Далее пусть
. Далее пусть 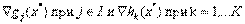 линейно независимы. Если х* — оптимальное решение задачи нелинейного программирования, то существует такая пара векторов
линейно независимы. Если х* — оптимальное решение задачи нелинейного программирования, то существует такая пара векторов 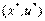 , что
, что 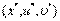 является решением задачи Куна—Таккера (3)—(7).
является решением задачи Куна—Таккера (3)—(7).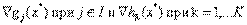 должны быть линейно независимыми, известно как условие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое почти всегда выполняется для встречающихся на практике задач оптимизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свойствами.
должны быть линейно независимыми, известно как условие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое почти всегда выполняется для встречающихся на практике задач оптимизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свойствами.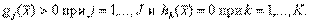

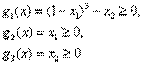
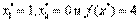 . Покажем, что условие линейной независимости не выполняется в точке оптимума.
. Покажем, что условие линейной независимости не выполняется в точке оптимума.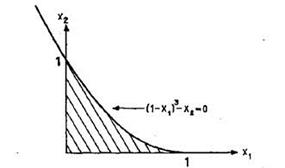
 Легко видеть, что векторы
Легко видеть, что векторы 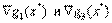 линейно зависимы, т. е. условие линейной независимости в точке
линейно зависимы, т. е. условие линейной независимости в точке 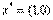 не выполняется.
не выполняется.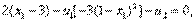 (11)
(11)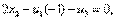 (12)
(12)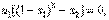 (13)
(13)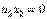 (14)
(14)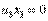 (15)
(15)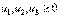 (16)
(16)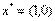 из уравнения (11) следует, что
из уравнения (11) следует, что 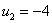 , тогда как уравнение (14) дает
, тогда как уравнение (14) дает 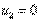 , Следовательно, точка оптимума не является точкой Куна — Таккера. Заметим, что нарушение условия линейной независимости не обязательно означает, что точка Куна—Таккера не существует. Для того чтобы подтвердить это, заменим целевую функцию из этого примера функцией
, Следовательно, точка оптимума не является точкой Куна — Таккера. Заметим, что нарушение условия линейной независимости не обязательно означает, что точка Куна—Таккера не существует. Для того чтобы подтвердить это, заменим целевую функцию из этого примера функцией 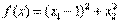 . При этом оптимум по-прежнему достигается в точке (1,0), в которой условие линейной независимости не выполняется. Условия Куна—Таккера (12) - (16) остаются неизменными, а уравнение (11) принимает вид
. При этом оптимум по-прежнему достигается в точке (1,0), в которой условие линейной независимости не выполняется. Условия Куна—Таккера (12) - (16) остаются неизменными, а уравнение (11) принимает вид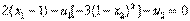
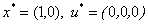 является точкой Куна—Таккера, т. е. удовлетворяет условиям Куна—Таккера.
является точкой Куна—Таккера, т. е. удовлетворяет условиям Куна—Таккера. , а ограничения в виде равенств содержат линейные функции
, а ограничения в виде равенств содержат линейные функции 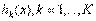 . Тогда если существует решение
. Тогда если существует решение 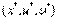 , удовлетворяющее условиям Куна—Таккера (3) — (7), то х* — оптимальное решение задачи нелинейного программирования.
, удовлетворяющее условиям Куна—Таккера (3) — (7), то х* — оптимальное решение задачи нелинейного программирования.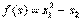
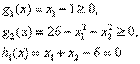
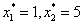 является оптимальным. Имеем
является оптимальным. Имеем
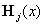 положительно полуопределена при всех х, функция
положительно полуопределена при всех х, функция 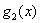 является вогнутой, вычислим
является вогнутой, вычислим
 отрицательно определена, функция
отрицательно определена, функция 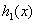 входит в линейное ограничение в вяде равенства. Следовательно, все условия теоремы 2 выполнены; если мы покажем, что
входит в линейное ограничение в вяде равенства. Следовательно, все условия теоремы 2 выполнены; если мы покажем, что 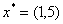 - точка Куна-Таккера, то действительно установим оптимальность решения
- точка Куна-Таккера, то действительно установим оптимальность решения 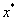 . Условия Куна-Таккера для примера 2 имеют вид
. Условия Куна-Таккера для примера 2 имеют вид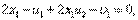 (22)
(22)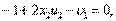 (23)
(23)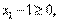 (24)
(24)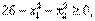 (25)
(25)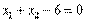 , (26)
, (26)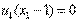 , (27)
, (27)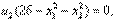 (28)
(28)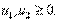 (29)
(29)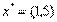 удовлетворяет ограничениям (24) — (26) и, следовательно, является допустимой. Уравнения (22) и (23) принимают следующий вид:
удовлетворяет ограничениям (24) — (26) и, следовательно, является допустимой. Уравнения (22) и (23) принимают следующий вид:
 ,получим
,получим 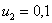 и
и 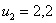 . Таким образом, решение х*=(1, 5),
. Таким образом, решение х*=(1, 5), 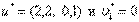 удовлетворяет условиям Куна—Таккера. Поскольку условия теоремы 2 выполнены, то
удовлетворяет условиям Куна—Таккера. Поскольку условия теоремы 2 выполнены, то 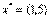 оптимальное решение задачи из примера 3. Заметим, что существуют также и другие значения
оптимальное решение задачи из примера 3. Заметим, что существуют также и другие значения 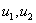 и
и