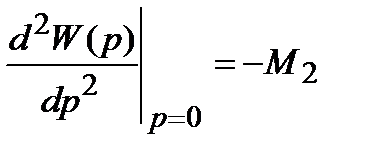|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Метод наименьших квадратов.
Метод последовательного логарифмирования. Метод последовательного логарифмирования применим для аппроксимации гладких неколебательных апериодических переходных процессов. Переходная функция должна быть представлена выражением вида:
где С0=h¥ »h(Ty), Сi и аi – вещественные числа, причем корни характеристического уравнения аi должны удовлетворять эмпирическому неравенству
Выражение есть решение линейного дифференциального уравнения порядка n с возмущающим ступенчатым воздействием. Требуется по таблично или графически заданной переходной функции объекта определить величины коэффициентов Сi, корни характеристического уравнения аi и порядок уравнения n. Суть метода заключается в последовательном приближении h(t) сначала решением уравнения первого порядка, то есть функцией Поэтому можно предположить, что h(t) есть решение линейного дифференциального уравнения первого порядка, и написать приближенное равенство.
Это соотношение верно при больших значениях времени t , когда влияние других составляющих
Отсюда нетрудно определить неизвестные величины α1 и С1. Для этого вычисляется функция h1(t)=C0-h(t) и строится график ln|h1(t)| в зависимости от времени t. При правильном определении параметров Сi и αi должны выполняться следующие условия:
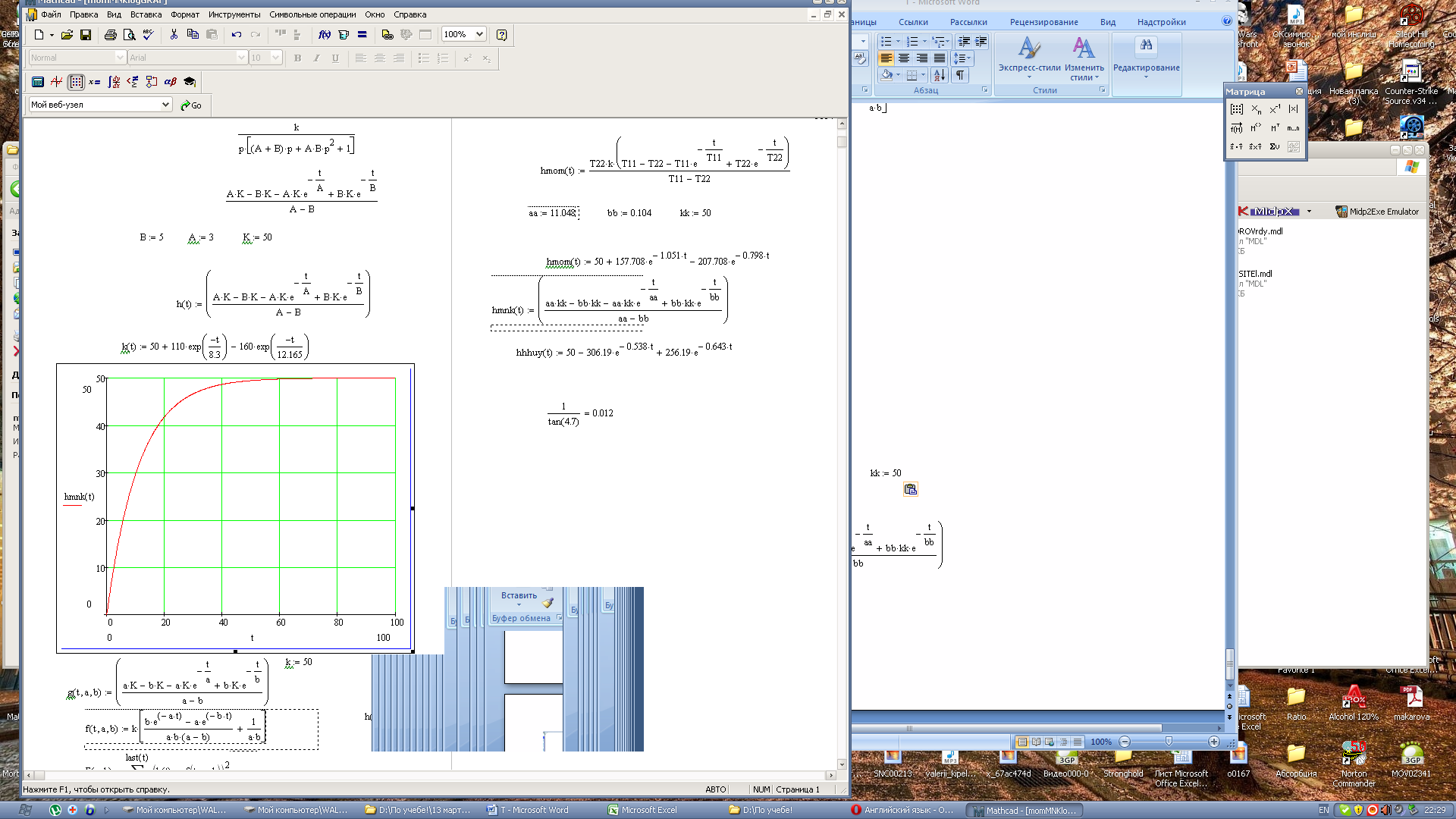
Рассчет в Exel. Данный метод реализован в EXEL и из-за относительно малого колличества шагов,взятых в Matlab график функции не достигает предела.
Ln(C1)=4,7 C1=110 Tg(a)=0,48/4=0,12 a=6,84 T1=1/Tg(a)=1/0,12=8,3 C0+C1+C2=0 50+110+C2=0 C2=-160 C1*a1+C2*a2=0 a2=-C1*a1/C2=4,7 Tg(a2)=0,0822 T2=1/Tg(a2)=12,165
Среднее квадратическое отклонение S=18,26238 Дисперсия D=333,5145
Метод наименьших квадратов. Число δ называется среднеквадратичным (или среднеквадратическим) уклонением функции Ф(х) от заданной f(x)
Наряду с δ вводят также вспомогательную величину:
Функцию Ф(х) стараются подобрать, чтобы число δ получилось достаточно малым. Для нашего случая функция Ф(х) примет вид:
Ф(х) найдена по МНК для f(x) если для нее сумма квадратов отклонений по всем узлам минимальна. Рассчет в Mathcad. Значениям t и h(t) соответствуют столбцы TOUT и SIMOUT(h(t)) взятые из Exсel, примененного в методе последовательного логарифмирования.
Метод моментов. При использовании метода моментов основной проблемой является нахождение функциональной зависимости между моментом входной и выходной функции. Получить явные выражения для моментов можно несколькими способами. Первый способ состоит в решении математической модели. Основным достоинством этого метода является возможность определения моментов как
для линейных, так и для нелинейных операторов, при любом промежутке интегрирования Т. Момент произвольной функции Ф интеграл вида
Однако в большинстве случаев получение решения уравнений математической модели в пространстве оригиналов представляет собой довольно сложную задачу. В связи с этим представляют значительный интерес методы, позволяющие определять моменты выходных кривых без предварительного получения решения уравнений модели в пространстве оригиналов. Оказывается, что для вычисления моментов функции достаточно знать ее изображение по Лапласу (которое часто найти гораздо легче, чем функцию). Действительно, согласно определению преобразования по Лапласу функции Ф(t), ее изображение
Это равенство при p=0 имеет вид
Найдем значение
Аналогично, для производных более высокого порядка получим:
Таким образом, для получения момента любого порядка некоторой функции Ф(t) достаточно продифференцировать по р необходимое число раз изображение Наша передаточная функция описывается уравнением апериодического звена второго порядка. Ее изображение по Лапласу имеет вид:
Тогда выражение примет вид:
Рассчитаем нулевой момент:
Рассчитаем первый момент (математическое ожидание):
С другой стороны, т.к. математическое ожидание – это среднее арифметическое значений импульсной переходной функции k(t)=C0-h(t)
Рассчитаем второй момент (дисперсию):
С другой стороны, т.к. дисперсия – это квадрат отклонения значений k(t) от среднего арифметического M1 .
Итак, получившаяся система уравнений позволяет найти T1 и T2, а следовательно и α1 и α2 .
Поиск по сайту: |
 ,
, ; i=1,2,…n-1
; i=1,2,…n-1 . Если эта аппроксимация неудовлетворительна на каком либо отрезке [0 , T], то вводится в рассмотрение вторая составляющая
. Если эта аппроксимация неудовлетворительна на каком либо отрезке [0 , T], то вводится в рассмотрение вторая составляющая  . Неизвестные αi и Ci определяются на каждом этапе аппроксимации с помощью операции логарифмирования, вследствие чего этот способ и получил свое название.
. Неизвестные αi и Ci определяются на каждом этапе аппроксимации с помощью операции логарифмирования, вследствие чего этот способ и получил свое название. или
или 
 можно пренебречь. Прологарифмируем функцию |h1(t)| и получим уравнение прямой линии в полулогарифмическом масштабе по оси ординат:
можно пренебречь. Прологарифмируем функцию |h1(t)| и получим уравнение прямой линии в полулогарифмическом масштабе по оси ординат:




























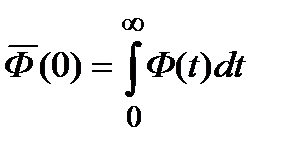 , т.е.
, т.е. 


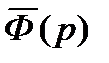 этой функции и положить р=0.
этой функции и положить р=0.