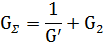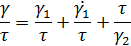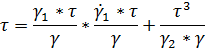Теоретические сведения. Изучение реологических моделей реальных тел

Изучение реологических моделей реальных тел

Цель работы.

а) Изучить методы математического описания различных материалов

б) Научиться составлять реологические модели по их феноменологическим (механическим) моделям.

Теоретические сведения

Реология – это наука, занимающаяся изучением закономерностей поведения различных материалов при разнообразном их деформировании. Деформациям сдвига нельзя считать бесконечно малыми, они возникают под воздействием касательного напряжения (1).

Деформации сдвига показана на рисунке1

а б

а - исходное состояние; б - схема деформируемого тела.

Рисунок 1 – иллюстрация деформации сдвига.

Относительная деформация сдвига (формула 1) двух элементарных слоев деформируемого сдвигового смещения слоя под действием касательных сил к его толщине:

(1)

Скорость деформации учитывают при изменении ее во времени в неустановившемся режиме. Если деформация при сдвиге под действием конечных сил увеличивается непрерывно, то материал начинает течь. При установившемся процессе деформирования изменение деформации в единицу времени постоянно, оно характеризуется градиентом скорости, которой по смыслу аналогичен скорости деформации (формула 2)

(2)

Различают два вида сдвиговых деформации: простой и сложный сдвиг. При

Сложный сдвиг возникает при одновременном воздействии на слой материала нескольких видов сил, например крутящий момент и его осевого давления, а при постом – действует либо осевое давление, либо крутящий момент.

Основной сдвиговой характеристикой материала является зависимость касательного напряжения (напряжение сдвига), вызывающего деформации, от сдвиговой деформации или ее скорости.

Основной сдвиговой характеристикой материала является зависимость касательного напряжения, вызывающего деформации, от сдвиговой деформации или скорости.

Для идеального упругого тела (тела Гука) связь напряжений и деформаций при чистом сдвиге описывается формулой 3

(3),

где G – модуль упругости второго рода, Па;

y – относительная деформация сдвига.

Тело Гука считается идеальным, так как оно восстанавливает свою исходную форму после снятия приложенных нагрузок. Кроме тела Гука, существуют еще две простейшие идеальные модели реальных тел – Сен-Венана и Ньютона.

Тело Сен-Венана представляет собой идеально пластичным, то есть до приложения силы оно идеально твердое и начинает деформироваться только после достижения предельного значения напряжения, например при чистом сдвиге . Величина и при этом не связана с .

Тело Ньютона – это идеально вязкая жидкость. У него скорости сдвиговых деформаций определяют возникающие касательные напряжения по формуле 4.

(4),

где - постоянный коэффициент, называемый коэффициентом вязкости.

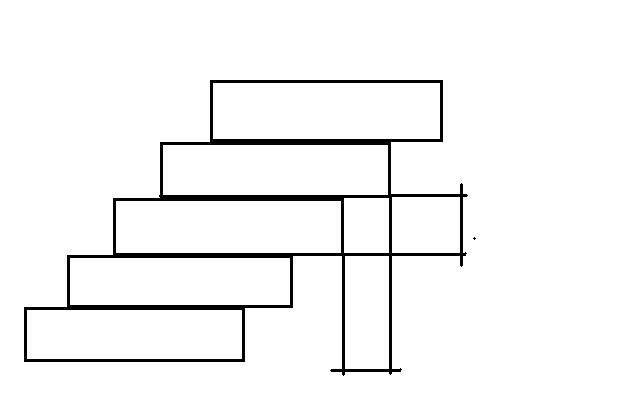
Реальные тела отличаются от идеальных тем, что в них одновременно присутствуют и упругие и пластические и вязкие свойства. Выражать реологические свойства реальных тел можно механическими моделями. Для тел Гука это пружина, Ньютона – это гидравлический амортизатор, для тела Сен-Венана поступательная кинематическая пара сухого трения. Условные изображения механических моделей реальных тел показаны на рисунке

Рисунок 2 - Механические модели реальных тел

а – тело Гука; б – тело Ньютона; в – тело Сен-Венана.

Из формул (3), (4) и рисунка 2 следует, что тело Гука характеризуется жесткостью пружины G, а тело Ньютона вязкостью .

Из элементов на рисунке 2 можно составить более сложные модели, например, тело Кельвина, изображенное на рисунке 3

Рисунок 3 - Механическая модель Кельвина

Для описания механической модели тела Кельвина используем условие: при параллельном соединении элементов деформация сложного тела равна деформации каждого элемента, а так напряжение суммарного элемента равно сумме напряжений в отдельных элементах и -формулы 5 и 6:

(5)

(6)

Воспользуемся реологическими уравнениями элементов Гука и Ньютона 7 и 8:

(7)

(8)

(9)

Кельвин ввел это идеальное тело для того, чтобы иметь возможность показать свойство вязкого трения для «твердого» тела, то есть явление ползучести, когда деформация развивается при величине приложенных напряжений.

Возможен другой способ сочетания упругих и вязких свойств, когда жидкость проявляет упругие свойства. Для описания такого явления можно взять другую реологическую модель – тело Максвелла, которое показано на рисунке 4.

Рисунок 4.Механическа модель тела Максвелла

Тело Максвелла описывается моделью стандартного линейного тела формула 10:

(10)

Решение уравнения (10) позволяет объяснить такое явление, как релаксация напряжений.

Практическое задание

Вывод: 1) Изучили методы математического описания различных материалов.

2) Научились составлять реологические модели по их феноменологическим (механическим) моделям.

Поиск по сайту: