 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теория метода и описание установки
Для определения ускорения силы тяжести можно воспользоваться методом маятника, который основан на зависимости периода колебания маятника от ускорения силы тяжести. Периодом колебания маятника называется время, в течение которого маятник совершит одно полное колебание, смещаясь сначала в одну, а затем в другую сторону от начального положения и снова возвращаясь к нему. Материальная точка, подвешенная на гибкой, невесомой и нерастяжимой нити, называется математическим маятником (рис. 1). В вертикальном положении сила тяжести материальной точки Р = mg полностью уравновешивается натяжением нити, и маятник остается в покое (положение равновесия - точка А). Если маятник отклонить от положения равновесия, например, в точку С, на некоторый угол а, то составляющая силы тяжести, направленная вдоль нити, т. е. сила
Длина дуги S = АС, на которую маятник отклонился от положения равновесия, называется смещением. Если смещение от А к С считать положительным, а от A к В — отрицательным, то сила всегда будет направлена обратно смещению 5 и при малых углах отклонения (5—6°) пропорциональна смещению, т. Таким образом так как Знак минус указывает, что сила Под действием такой силы математический маятник совершает гармоническое колебательное движение. Коэффициент Если в формулу (1) подставить значение К и α, при чем угол а выразить в радианах, т. е. Отсюда период колебания математического маятника
где g - ускорение силы тяжести; l - длина математического маятника. Эту формулу можно применять как к математическому, так и к физическому маятникам, но для физического маятника длина обозначает так называемую приведенную длину физического маятника. Приведенной длиной физического маятника называется длина некоторого воображаемого математического маятника, который имеет тот же период колебаний, что и данный физический маятник. На практике приведенная длина физического маятника определяется расстоянием между точкой подвеса маятника и его центром качания (точкой, находящейся от точки подвеса на расстоянии, равном приведенной длине маятника). Центр качания лежит ниже центра тяжести маятника. Маятник, вся масса которого была бы сосредоточена в центре качания, имел бы тот же период, что и математический маятник данной длины. Период колебания физического маятника
где lпр - приведенная длина маятника. Решая эту формулу относительно g, будем иметь
Таким образом, задача нахождения g сводится к определению приведенной длины маятника и его периода. Маятник, применяемый в физических лабораториях, представляет собой массивный шарик небольшого радиуса, подвешенный на длинной двойной нити для того, чтобы колебания происходили строго в одной плоскости. В данном случае конструктивное оформление установки следующее: на перекладине между двумя жестко укрепленными вертикальными стойками подвешен на двойной нити свинцовый шарик А. Вдоль вертикальных стоек перемещается при помощи скользящих муфт вторая горизонтальная перекладина - линейка В, которая может быть закреплена на любой высоте при помощи винта в одной из муфт (рис.2). На стойках нанесена сантиметровая, а с перемещающейся линейкой скреплена миллиметровая шкала. Приведенной длиной маятника следует считать расстояние от точки подвеса О до центра качания шарика. Однако непосредственно определить приведенную длину маятника сложно, поэтому поступают следующим образом: подводят подвижную линейку до соприкосновения с шариком и измеряют Длину колебаний T1 и T2 маятников двух различных приведенных длин Из формулы (3) имеем
Вычитая (3") из (3'), получим:
Откуда
Таким образом, для определения g по формуле (4) нужно измерить лишь разности длин
Поиск по сайту: |
 уравновесится натяжением нити Т2, другая же составляющая, т. е. сила
уравновесится натяжением нити Т2, другая же составляющая, т. е. сила 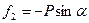 , перпендикулярная к нити, стремится вернуть маятник в положение равновесия. Эта сила является равнодействующей веса и реакции нити. Она называется квазиупругой силой (упругоподобной).
, перпендикулярная к нити, стремится вернуть маятник в положение равновесия. Эта сила является равнодействующей веса и реакции нити. Она называется квазиупругой силой (упругоподобной).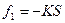 .
.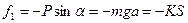 , (1)
, (1)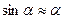 .
.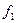 должна быть направлена против смещения S, т. е. к положению равновесия.
должна быть направлена против смещения S, т. е. к положению равновесия.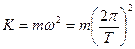 играет роль коэффициента квазиупругой силы.
играет роль коэффициента квазиупругой силы. , то формула примет вид:
, то формула примет вид: 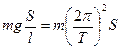 .
.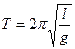 , (2)
, (2)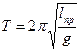
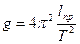 (3)
(3)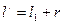 , где r ≈ радиус шарика, и длину
, где r ≈ радиус шарика, и длину 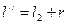 . Затем рассчитывают периоды
. Затем рассчитывают периоды и
и  .
.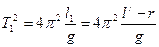 ; (3/)
; (3/)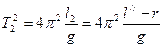 . (3//)
. (3//)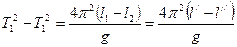 ,
, . (4)
. (4)