 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
При равномерном вращении угловая скоростьСтр 1 из 2Следующая ⇒
КРАТКАЯ ТЕОРИЯ В механике твердого тела рассматривается движение абсолютно твердого тела, т.е. такая система материальных точек, при любых движениях которой взаимное расстояние между ними остается неизменным. Иначе говоря, размеры и форма абсолютно твердого тела не изменяются при его движении. В природе нет абсолютно твердых тел – это физическая абстракция. Всякое тело под действием приложенных к нему сил в большей или меньшей степени деформируется, т.е. изменяет свою форму и размеры. Однако в тех случаях, когда деформация тела при его движении пренебрежимо малы, тело можно считать абсолютно твердым. Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное. Поступательное движение – это такое движение, при котором любая прямая, соединяющая две точки тела, остается параллельной самой себе. Вращательнымдвижением называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться и вне тела. Окружности, описываемые точками вращающегося тела, располагаются в плоскостях, перпендикулярных к оси вращения. Рассмотрим кинематику вращательного движения твердого тела.
Рис. 1
Величина элементарного перемещения точки А вращающегося твердого тела dS = где Так как
- угловая скорость, равная производной от углового перемещения от времени. При равномерном вращении угловая скорость
т.е. равна углу поворота за единицу времени. Размерность Для полноты характеристики вращательного движения должно быть указано не только числовое значение угловой скорости, но и ориентация оси вращения и направление вращения. Задать все эти характеристики одновременно можно, рассматривая угловую скорость как вектор. Вектор угловой скорости Если направление вращения ручки буравчика (с правовинтовой нарезкой) совпадает с направлением вращения тела, то направление поступательного движения буравчика совпадает с направлением вектора угловой скорости
Рис. 2
Установим связь между направлениями векторов Расположение этих векторов указано на рис. 3
Рис. 3
Как видно, вектор Если радиус-вектор
При неравномерном вращении быстроту изменения угловой скорости характеризуют величиной, которую называют угловым ускорением. Вектор углового ускорения определяют как производную от угловой скорости по времени.
В случае неподвижной оси, когда векторы
Если угловая скорость возрастает по величине, то вектор углового ускорения
Ускоренное движение Рис. 4
Замедленное движение Рис. 5
Рис. 6
Если же угловая скорость В случае неподвижной оси Перейдем теперь к динамике твердого тела. Сначала рассмотрим движение одной материальной точки массы m, движущейся по окружности радиуса r вокруг оси вращения. 2-й закон Ньютона для движения материальной точки под действием силы
После векторного умножения на
Приняв во внимание, что И Поэтому Величина Векторное произведение
Рис. 7
Из рис. 7 и по определению векторного произведения видно, что численное значение момента силы Если
Точно также и Так как для точки, вращающейся по окружности, Величина Таким образом, уравнение движения материальной точки по окружности может быть записано и в следующем виде:
Уравнение движения вращающегося тела, которое можно рассматривать как систему материальных точек, движущихся по окружности, можно получить, суммируя уравнение (11) по всем точкам тела:
Для абсолютно твердого тела Величина
где интегрирование должно быть распространено на все элементы тела. Уравнение движения вращающегося твердого тела (основной закон динамики вращательного движения), таким образом, имеет вид:
где Если мы сравним уравнение (13) с уравнением Отметим, что понятие момента инерции ( формула (12)) было введено выше при рассмотрении вращения твердого тела. Однако следует иметь в виду, что эта величина существует безотносительно к вращению. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находится в состоянии покоя. Момент инерции тела относительно какой – либо оси можно найти вычислением или измерить экспериментально. Если вещество в теле распределено непрерывно, то определение момента инерции сводится к вычислению интеграла (12). Аналитическое вычисление таких интегралов возможно только в простейших случаях тел симметричной формы. Для тел неправильной формы такие интегралы могут быть найдены численно. Вычисление моментов инерции относительно произвольной оси во многих случаях можно упростить, если воспользоваться теоремой Штейнера, котораяформулируется следующим образом: момент инерции
Момент импульса твердого телаотносительно центра вращения «0» складывается из моментов импульса, составляющих его материальных точек (формула (9)):
Из приведенного выражения видно, что в общем случае направление вектора 1) Центром масс или центром инерции системы называется такая точка, радиус-вектор
Можно показать, что для каждого тела существуют, по крайней мере, три взаимно перпендикулярных направления в пространстве – оси, при вращении вокруг которых момент импульса параллелен В этом случае
и точка «0», являющаяся точкой пересечения осей совпадает с центром инерции. Такие оси носят название свободных осей . При вращении вокруг свободной оси не возникает моментов сил, стремящихся деформировать ось, и в отсутствие внешних сил ось сохраняет свое положение в пространстве. Если тело обладает осью симметрии, то одна из свободных осей совпадет с ней. Пользуясь понятием момента импульса тела, можно представить основное уравнение динамики (13) для тела, вращающегося вокруг неподвижной оси
В случае, когда результирующий момент внешних сил, действующих на систему, равен нулю (
Это следствие уравнения (16) носит название закона сохранения момента импульса. Отметим, что момент силы будет равен нулю не только, когда внешние силы отсутствуют, но и когда эти силы имеют направление, параллельное оси вращения или проходящее через нее. Кинетическая энергия твердого тела, вращающегося вокруг оси, складывается из кинетических энергий материальных точек, составляющих это тело:
При вращении абсолютно твердого тела все точки тела имеют одинаковую угловую скорость В общем случае движения, полная кинетическая энергия твердого тела складывается из кинетической энергии его поступательного движения со скоростью движения его центра инерции
1. ЦЕЛЬ И СОДЕРЖАНИЕ РАБОТЫ Целью работы является изучение движения гироскопа. Содержание работы состоит в определении угловой скорости прецессии гироскопа.
Поиск по сайту: |

 АА/ связана с угловым перемещением
АА/ связана с угловым перемещением 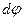 , совершаемым за бесконечно малый промежуток времени dt , формулой:
, совершаемым за бесконечно малый промежуток времени dt , формулой: 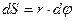 (1)
(1) - радиус окружности, описываемой точкой А.
- радиус окружности, описываемой точкой А. - линейная скорость данной точки вращающегося тела, то
- линейная скорость данной точки вращающегося тела, то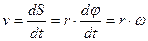 (2) где
(2) где 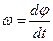 (3)
(3)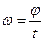 (4)
(4)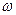 равна
равна 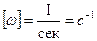
 направлен по оси вращения, и его направление определяется по правилу буравчика.
направлен по оси вращения, и его направление определяется по правилу буравчика.
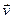 ,
, 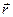 .
.
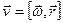 т.е.
т.е.  (5)
(5)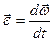 :
:  .
.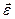 направлены по оси вращения, вектор тангенциального ускорения и вектор углового ускорения связаны следующим соотношением:
направлены по оси вращения, вектор тангенциального ускорения и вектор углового ускорения связаны следующим соотношением: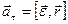
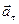 направлен по касательной в ту же сторону, что и линейная скорость (рис. 4).
направлен по касательной в ту же сторону, что и линейная скорость (рис. 4).
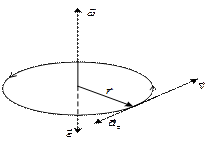
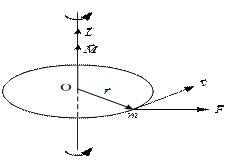
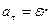 (6)
(6)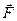 , расположенной в плоскости, перпендикулярной оси вращения, имеет вид
, расположенной в плоскости, перпендикулярной оси вращения, имеет вид (7)
(7)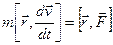
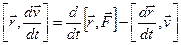
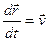 , а
, а 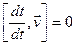 , получаем
, получаем  .
.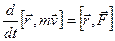 ,или
,или 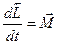 (8)
(8) (9)называется моментом импульса точки относительно оси вращения.
(9)называется моментом импульса точки относительно оси вращения.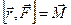 называется моментом силы относительно той же оси. Вектор момента силы и вектор момента импульса направлены по оси вращения (рис. 6 ).
называется моментом силы относительно той же оси. Вектор момента силы и вектор момента импульса направлены по оси вращения (рис. 6 ).
 , то
, то 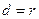 и, следовательно,
и, следовательно, (10)
(10)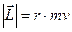 , если
, если 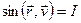 . Для этого случая можно записать
. Для этого случая можно записать 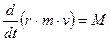 \Или, поскольку
\Или, поскольку  , то
, то 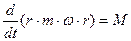
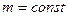 , а
, а  , то можно записать
, то можно записать 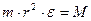
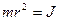 называется моментом инерции материальной точкиотносительно оси вращения.
называется моментом инерции материальной точкиотносительно оси вращения.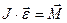 (11)
(11)
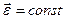 , тогда
, тогда 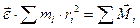
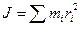 называется моментом инерции телаотносительно оси. Если тело сплошное, то его разбивают на отдельные элементы, настолько малые, что их можно считать точками, и момент инерции тогда определяется следующим образом:
называется моментом инерции телаотносительно оси. Если тело сплошное, то его разбивают на отдельные элементы, настолько малые, что их можно считать точками, и момент инерции тогда определяется следующим образом: (12)
(12) - результирующий момент внешних сил, действующих на данное тело, т.к. сумма моментов внутренних сил равна 0.
- результирующий момент внешних сил, действующих на данное тело, т.к. сумма моментов внутренних сил равна 0. для поступательного движения твердого тела, то мы увидим, что момент инерции тела характеризует инертность тела во вращательном движении подобно массе тела в поступательном движении. Роль силы при вращательном движении играет момент силы, а линейного ускорения – угловое ускорение.
для поступательного движения твердого тела, то мы увидим, что момент инерции тела характеризует инертность тела во вращательном движении подобно массе тела в поступательном движении. Роль силы при вращательном движении играет момент силы, а линейного ускорения – угловое ускорение.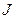 относительно произвольной оси равен сумме момента инерции
относительно произвольной оси равен сумме момента инерции 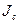 относительно оси, параллельной данной и проходящей через центр тела, и произведения массы тела «m» квадрат расстояния «а» между осями:
относительно оси, параллельной данной и проходящей через центр тела, и произведения массы тела «m» квадрат расстояния «а» между осями: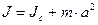 (14)
(14)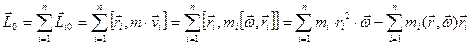
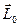 не совпадает с вектором угловой скорости
не совпадает с вектором угловой скорости  которой выражается через векторы
которой выражается через векторы  ,
,  , … отдельных материальных точек системы по формуле:
, … отдельных материальных точек системы по формуле: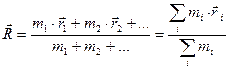
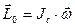 (15)
(15)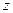 в следующем виде:
в следующем виде: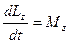 (16)
(16)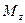 =0), то
=0), то
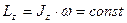 (17)
(17)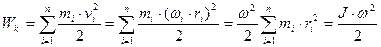 (18)
(18)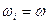
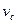 и кинетической энергии вращения вокруг оси, проходящей через центр инерции:
и кинетической энергии вращения вокруг оси, проходящей через центр инерции: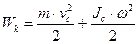 .
.