 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
II. Краткая теория работы
В настоящей работе определяется зависимость пути от времени для равноускоренного движения при помощи машины Атвуда. Машина Атвуда (рис. 1) состоит из легкого блока в виде сплошного диска, способного вращаться вокруг неподвижной горизонтальной оси, расположенной в верхней части вертикальной стойки. На правой стороне стойки нанесена шкала с сантиметровыми отметками. Через блок перекинута легкая капроновая нить, на концах которой закреплены грузики в виде цилиндров разной массы В левой верхней части стойки установлено электромагнитное пусковое устройство, позволяющее фиксировать положение грузиков, зажимая нить между двумя дисками, один из которых связан с электромагнитом. При освобождении нити грузики приходят в движение, одновременно включается электронный секундомер. Пройдя путь Закон движения грузиков в первом приближении можно записать в виде:
Этот закон вытекает из законов поступательного и вращательного движения блока и грузиков с учетом связи тангенциального и углового ускорения тел:
Где J- момент инерции блока, R- радиус блока, g- ускорение свободного падения. Трением в оси блока пренебрегаем. Величина пути
. Однако ряд причин случайного характера (например, неточность начального расположения правого грузика на заданном расстоянии
Рис 1. Машина Атвуда
1 – блок, 2 – грузики, 3 – нить, 4 – электромагнит, 5 – неподвижная платформа с контактным устройством, 6 – стойка со шкалой, 7 – подставка.
Введем параметр
Преобразовав это выражение, получим:
Усредняя эту зависимость по случайным значениям параметра
Если распределение случайной величины
Этот закон содержит два параметра:
Поиск по сайту: |
 и
и 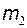 .
. , правый цилиндрик попадает своим нижним основанием на горизонтальную неподвижную платформу и замыкает контакты, останавливающие секундомер.
, правый цилиндрик попадает своим нижним основанием на горизонтальную неподвижную платформу и замыкает контакты, останавливающие секундомер. (1).
(1). :
:
 , определяется (из кинематики) уравнением:
, определяется (из кинематики) уравнением: . (2).
. (2).
 – случайную величину, характеризующую неопределенность моментов начала и конца движения. Тогда,
– случайную величину, характеризующую неопределенность моментов начала и конца движения. Тогда,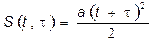 . (3)
. (3) . (4)
. (4) . (5)
. (5) (то есть положительные и отрицательные значения
(то есть положительные и отрицательные значения  ,
,  , следовательно, введя обозначения
, следовательно, введя обозначения  и
и  , можно записать:
, можно записать: . (6)
. (6) – начальное смещение и
– начальное смещение и  – величину, равную половине ускорения. Эти параметры определяются по измеренным значениям пройденного пути
– величину, равную половине ускорения. Эти параметры определяются по измеренным значениям пройденного пути  и сериям значений промежутков времени
и сериям значений промежутков времени  методом наименьших квадратов (см. Приложение 1).
методом наименьших квадратов (см. Приложение 1).