 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
эквивалентная схема биполярного транзистора
Анализ работы усилителя в широком диапазоне частот можно осуществить на основе метода эквивалентных схем, являющегося одним из наиболее распространенных расчетных методов теории электрических цепей. Поскольку электронные усилители строятся на основе биполярных и полевых транзисторов, и пассивных радиоэлементов, то на первом этапе необходимо получить эквивалентную схему активного элемента – транзистора. Эквивалентную схему транзистора можно получить, если воспользоваться некоторыми методами теории электрических цепей, в частности, методами анализа линейных активных четырехполюсников. Четырехполюсником называется устройство, которое имеет две точки входа и две точки выхода. Биполярный и полевой транзисторы в любой схеме включения представляют собой четырехполюсник. Различают пассивные и активные четырехполюсники. Пассивные четырехполюсники не содержат источников напряжения или тока. Каскад усилителя на биполярном или полевом транзисторе способен усиливать мощность входного сигнала и является активным четырехполюсником. Теория четырехполюсников разработана для линейных систем, для которых характерна линейная зависимость между током и напряжением. Биполярный и полевой транзисторы являются нелинейными элементами. Однако, при работе в режиме малого сигнала, характерном для усилителей напряжения, усилитель на транзисторе можно считать линейным устройством, и применить к нему теорию линейных четырехполюсников. На рис. 5.6 представлена эквивалентная схема линейного четырехполюсника. Каждый четырехполюсник характеризуется четырьмя величинами: током и напряжением на входе и током и напряжением на выходе.
Рис. 5.6.Эквивалентная схема четырехполюсника В теории четырехполюсников зависимости между входными и выходными токами и напряжениями анализируют, используя режимы холостого хода и короткого замыкания на входе и выходе четырехполюсника. В результате параметры транзистора находятся из соответствующих уравнений для токов и напряжений. Поскольку к четырехполюсникам относятся различные по физическим принципам функционирования устройства, то уравнения для токов и напряжений будут в каждом случае разными. Существует шесть различных систем уравнений, описывающих связь токов и напряжений для разных видов четырехполюсников. Будем рассматривать биполярный транзистор в схеме с общим эмиттером как активный линейный четырехполюсник.
Рис. 5.7. Транзистор по схеме с общим эмиттером как четырехполюсник Особенности биполярных транзисторов наилучшим образом учитываются системой уравнений в
Для малых приращений переменных токов и напряжений запишем уравнения в полных дифференциалах:
Частные производные, вычисленные в окрестности рабочей точки транзистора, представляют собой некоторые постоянные величины –
Для транзистора по схеме с ОЭ уравнения можно записать в следующем виде:
Биполярные транзисторы отличаются небольшим значением входного сопротивления и сравнительно высоким значением выходного сопротивления. Поэтому в такой схеме для нахождения Осуществляя режим холостого хода на входе четырехполюсника, найдем из уравнений 5.18 и 5.19 параметры
Два оставшихся параметра можно найти, осуществив режим короткого замыкания на выходе четырехполюсника. При коротком замыкании на выходе
Так как мы рассматриваем построение эквивалентной схемы биполярного транзистора для переменных составляющих токов и напряжений, то все токи и напряжения в уравнениях в
Параметр Параметр Параметр Параметр Определение Токов и напряжений, представлена на рис.5.8.
Рис.5.8. Эквивалентная схема биполярного транзистора Проводя аналогичные рассуждения, можно получить эквивалентную схему полевого транзистора, представляя полевой транзистор, включенный по схеме с общим истоком, в виде линейного активного четырехполюсника, как показано на рис. 5.9.
Рис. 5.9. Полевой транзистор как линейный четырехполюсник Особенности полевых транзисторов наилучшим образом учитываются системой уравнений в
Для малых приращений переменных токов и напряжений запишем уравнения в полных дифференциалах:
Частные производные, вычисленные в окрестности рабочей точки, представляют собой некоторые постоянные величины –
Полевые транзисторы отличаются высокими значениями величин входного и выходного сопротивлений. Поэтому для нахождения При коротком замыкании на входе
Условие Для схемы с ОИ уравнения можно записать в следующем виде:
Из этих уравнений можно выяснить физический смысл
Крутизну и внутреннее сопротивление полевого транзистора можно найти из семейства выходных характеристик. Заменяя в системе уравнений приращения переменных составляющих токов и напряжений конечными значениями токов и напряжений, можно записать уравнения в следующем виде:
Определение
Рис.5.10. Эквивалентная схема полевого транзистора В результате анализа мы получили похожие эквивалентные схемы для биполярного и полевого транзисторов. В правых частях эквивалентных схем включены генераторы, которые отражают усилительные свойства активных элементов. В левых частях схем включены генераторы, отражающие внутреннюю обратную связь в активных элементах. Поскольку коэффициенты внутренней обратной связи достаточно малы, в дальнейшем анализе будем пренебрегать их величиной. С учетом этого можно исключить эти генераторы из левых частей эквивалентных схем и предложить единую упрощенную эквивалентную схему для биполярного и полевого транзисторов, представленную на рис. 5.11. Эта схема включает в себя входное и выходное сопротивление транзистора и генератор тока
Рис. 5.11. Эквивалентная схема биполярного и полевого транзисторов
Поиск по сайту: |



 - параметрах. Для схемы с ОЭ в этой системе за независимые переменные берутся входной ток
- параметрах. Для схемы с ОЭ в этой системе за независимые переменные берутся входной ток  И выходное напряжение
И выходное напряжение  , а зависимыми будут входное напряжение
, а зависимыми будут входное напряжение  и выходной ток
и выходной ток  . Таким образом, можно записать:
. Таким образом, можно записать: (5.12)
(5.12) (5.13)
(5.13) (5.14)
(5.14) (5.15)
(5.15) , (5.16)
, (5.16) . (5.17)
. (5.17) , (5.18)
, (5.18) . (5.19)
. (5.19) и
и  при
при  и выясним их физический смысл:
и выясним их физический смысл: - величина, обратная коэффициенту усиления по напряжению при разомкнутой входной цепи, характеризует внутреннюю обратную связь в биполярном транзисторе;
- величина, обратная коэффициенту усиления по напряжению при разомкнутой входной цепи, характеризует внутреннюю обратную связь в биполярном транзисторе; =
=  - выходная проводимость транзистора при разомкнутой входной цепи.
- выходная проводимость транзистора при разомкнутой входной цепи. 0. Тогда из уравнений 5.18 и 5.19 найдем:
0. Тогда из уравнений 5.18 и 5.19 найдем: =
= 
 - дифференциальное входное сопротивление транзистора при коротком замыкании на выходе;
- дифференциальное входное сопротивление транзистора при коротком замыкании на выходе; =
=  - коэффициент усиления тока базы транзистора при коротком замыкании на выходе.
- коэффициент усиления тока базы транзистора при коротком замыкании на выходе. 0 соответствует условию
0 соответствует условию  для постоянной составляющей, величина которой определяется напряжением смещения. Условие для переменного напряжения
для постоянной составляющей, величина которой определяется напряжением смещения. Условие для переменного напряжения  =0 соответствует условию
=0 соответствует условию  Для постоянного напряжения на коллекторе. При этих условиях
Для постоянного напряжения на коллекторе. При этих условиях 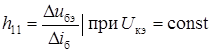 , (5.20)
, (5.20) , (5.21)
, (5.21) , (5.22)
, (5.22) . (5.23)
. (5.23) имеет размерность сопротивления и для его определения необходимо иметь семейство входных характеристик транзистора.
имеет размерность сопротивления и для его определения необходимо иметь семейство входных характеристик транзистора. .
.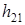 также является безразмерной величиной и его можно определить по семейству выходных характеристик.
также является безразмерной величиной и его можно определить по семейству выходных характеристик. на выходе транзистора зависит от двух составляющих: управляемого генератора тока
на выходе транзистора зависит от двух составляющих: управляемого генератора тока  и величины
и величины  , определяемой выходной проводимостью. Поэтому в выходную цепь эквивалентной схемы транзистора надо включить управляемый генератор тока и выходную проводимость. Эквивалентная схема биполярного транзистора, составленная на основе уравнений 5.18 и 5.19, при замене приращений переменных составляющих токов и напряжений конечными значениями
, определяемой выходной проводимостью. Поэтому в выходную цепь эквивалентной схемы транзистора надо включить управляемый генератор тока и выходную проводимость. Эквивалентная схема биполярного транзистора, составленная на основе уравнений 5.18 и 5.19, при замене приращений переменных составляющих токов и напряжений конечными значениями

 - параметрах. Для схемы с ОИ в этой системе за независимые переменные берутся входное напряжение
- параметрах. Для схемы с ОИ в этой системе за независимые переменные берутся входное напряжение  , (5.24)
, (5.24) . (5.25)
. (5.25) , (5.26)
, (5.26) . (5.27)
. (5.27) , (5.28)
, (5.28)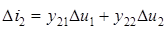 . (5.29)
. (5.29)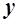 -параметров необходимо осуществить режим короткого замыкания на входе и на выходе четырехполюсника.
-параметров необходимо осуществить режим короткого замыкания на входе и на выходе четырехполюсника. 0, а при коротком замыкании на выходе
0, а при коротком замыкании на выходе  =0. При этом из уравнений (5.28), (5.29) можно найти
=0. При этом из уравнений (5.28), (5.29) можно найти 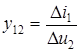 ,
,  ,
,  ,
,  .
. 0 означает, что равна нулю переменная составляющая выходного напряжения, а постоянная составляющая равна напряжению на стоке транзистора.
0 означает, что равна нулю переменная составляющая выходного напряжения, а постоянная составляющая равна напряжению на стоке транзистора. , (5.30)
, (5.30)  . (5.31)
. (5.31) - входная проводимость. Величина обратная входной проводимости равна входному сопротивлению полевого транзистора;
- входная проводимость. Величина обратная входной проводимости равна входному сопротивлению полевого транзистора;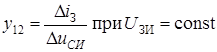 - коэффициент внутренней обратной связи между выходной и входной цепями полевого транзистора. Его величина составляет, примерно,
- коэффициент внутренней обратной связи между выходной и входной цепями полевого транзистора. Его величина составляет, примерно, 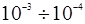 ;
; - крутизна
- крутизна  полевого транзистора;
полевого транзистора; - выходная проводимость. Величина обратная выходной проводимости равна внутреннему сопротивлению полевого транзистора
- выходная проводимость. Величина обратная выходной проводимости равна внутреннему сопротивлению полевого транзистора  .
. , (5.32)
, (5.32) . (5.33)
. (5.33) и эквивалентный генератор тока
и эквивалентный генератор тока 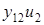 =
=  , отражающий внутреннюю обратную связь в полевом транзисторе. Второе уравнение (5.33) позволяет описать выходную часть эквивалентной схемы, включающую в себя выходную проводимость
, отражающий внутреннюю обратную связь в полевом транзисторе. Второе уравнение (5.33) позволяет описать выходную часть эквивалентной схемы, включающую в себя выходную проводимость  и эквивалентный генератор тока
и эквивалентный генератор тока  , характеризующий усилительные свойства полевого транзистора.
, характеризующий усилительные свойства полевого транзистора.
 , характеризующий усилительные свойства активного элемента. Для биполярного транзистора
, характеризующий усилительные свойства активного элемента. Для биполярного транзистора  , а для полевого транзистора
, а для полевого транзистора  .
.