 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Непрерывная случайная величина X имеет нормальное распределение, если ее плотность распределения вероятности имеет вид:
где График дифференциальной функции распределения называют нормальной кривой, или кривой Гаусса (рис.1).
Рис.1 Если Вероятность попадания нормально распределенной случайной величины в интервал (
Данный интеграл выражается через функцию Лапласа, которую еще называют интегралом вероятностей и обозначают Ф(t): Ф(t) Функция Лапласа – это вероятность попадания нормированной нормально распределенной случайной величины в интервал ( 0, t). Функция Лапласа обладает следующими свойствами: 1. Ф(0) = 0. 2. Ф(–t) = –Ф(t), то есть она нечетная. 3. Ф(¥) = 0,5 (практически уже при t > 4). Функция Ф(t) табулирована (см. прил. 2). Применяя функцию Лапласа, получим:
При решении задач часто возникает необходимость определения вероятности отклонения нормально распределенной случайной величины от ее математического ожидания:
Пример 1. Средний процент выполнения плана некоторыми предприятиями составляет 105 %, среднее квадратическое отклонение – 5 % . Полагая, что выполнение плана предприятиями подчинено закону нормального распределения, вычислить долю предприятий, выполняющих план от 110 до 130 %, то есть определить вероятность попадания рассматриваемой величины в интервал ( 110, 130). Решение. Случайная величина X – выполнение плана предприятиями; она имеет нормальное распределение с параметрами:
Пример 2. Длина изготовляемой детали представляет собой случайную величину, распределенную по нормальному закону. Средняя длина детали равна 50 мм, а дисперсия – 0,25 мм2. Какое поле допуска длины изготовляемой детали можно гарантировать с вероятностью 0,99? Решение. Длина изготовляемой детали – случайная величина X, имеющая нормальный закон распределения с параметрами:
Известна вероятность, гарантирующая некоторое поле допуска, то есть Р(a< X< b) = 0,99. Чтобы найти это поле допуска, воспользуемся формулой:
Неравенство ½X– Исходя из условия задачи, можем записать:
По таблице значений функции Лапласа (см. прил. 2) находим Отсюда e = 2,58 ×
Поиск по сайту: |

 и
и  – параметры распределения, причем
– параметры распределения, причем 
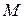 (X) = 0,
(X) = 0,  табулирована.
табулирована. ,
,  ) находим по формуле:
) находим по формуле:
 .
.

 Для нахождения искомой вероятности воспользуемся формулой:
Для нахождения искомой вероятности воспользуемся формулой:

 = 0,5.
= 0,5.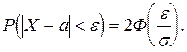
 , следовательно, и равновероятно, то есть
, следовательно, и равновероятно, то есть 
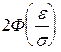 = 0,99;
= 0,99;  = 0,495.
= 0,495. = 2,58.
= 2,58.