 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задания для самостоятельной работы. Тема: Средние величины
Тема: Средние величины Цель занятия: Освоение методики вычисления средних величин. План занятия: I. Рассмотрение теоретических основ вычисления и использования средних величин. 1. Средние величины, их виды и область применения. 2. Вариационный ряд, методика его построения и характеристика. 3. Методы вычисления средней арифметической (средней арифметической простой и взвешенной, по способу моментов). 4. Среднеквадратическое отклонение, методика его вычисления и область применения. 5. Методика вычисления и использование коэффициента вариации. II. Методика вычисления средних величин, среднеквадратических отклонений. Основные понятия и определения по теме Для характеристики изучаемой совокупности по количественным признакам используются различные показатели, в том числе и средние величины, которые показывают средний уровень изучаемого признака. Средние величины используются в здравоохранении: – для оценки здоровья населения (показатели физического развития, средняя длительность пребывания на больничном листе и т.д.); – для оценки деятельности лечебно-профилактических учреждений (средняя длительность работы койки в году, оборот койки и т.д.); – для планирования (число жителей на терапевтическом, педиатрическом участке, стоимость одного койко-дня и т.д.); – для оценки санитарно-гигиенических параметров (освещенность, температура, влажность воздуха и т.д.); – для определения разовых доз лекарственных веществ и т.д. Средний уровень изучаемого явления – одно из групповых свойств статистической совокупности. Средний уровень измеряют с помощью критериев, которые носят название средних величин. Средние величины обладают тремя свойствами: – средняя занимает срединное положение в вариационном ряду; – средняя выражает общую меру изучаемого явления; – сумма отклонений всех вариант от средней равна нулю. Наиболее широко используются три средние величины: – мода (Мо) – соответствует величине признака, который чаще встречается в статистической совокупности, т.е. варианте наиболее часто встречающейся в вариационном ряду; – медиана (Ме) – варианта, занимающая срединное положение в вариационном ряду и делящая его пополам. Для того, чтобы узнать значение медианы, необходимо определить порядковый номер варианты, занимающей срединное положение (n/2), где n – число вариант в вариационном ряду. При нечетном числе вариант используется формула n+1/2; – средняя арифметическая (простая, взвешенная). Для определения средних величин в статистической совокупности необходима предварительная обработка и систематизация данных исследования, а именно, построение вариационного ряда. Вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по величине и расположенных в определенном порядке. Вариационный ряд может быть: – простой, несгруппированный; – сгруппированный; – прерывный или непрерывный; – правильный или неправильный; – ранжированный или неранжированный. Обозначения, используемые в вариационном ряду: – варианта (V) – отдельное числовое выражение изучаемого признака; – частота (р) – количество вариант определенной величины; – число наблюдений (n) – общее число вариант в вариационном ряду. Если число наблюдений не превышает 30, то варианты можно расположить по возрастанию или убыванию, т.е. построить простой вариационный ряд. Пример: получены данные о длительности лечения в поликлинике 45 больных ангиной (в днях): 20, 18, 19, 16, 17, 16, 14, 13, 15, 14, 15, 13, 12, 13, 3, 4, 12, 11, 12, 11, 10, 12, 11, 10, 11, 8, 7, 11, 11, 10, 10, 10, 9, 8, 8, 9, 4, 5, 6, 9, 5, 9, 6, 7, 7. Строим вариационный ряд: Таблица 1
Определяем средние величины: Мода (Мо) =11, т.к. данная варианта встречается в вариационном ряду наиболее часто (р=6). Медиана (Ме) – порядковый номер варианты занимающей срединное положение Средняя арифметическая (М) позволяет наиболее полно охарактеризовать средний уровень изучаемого признака. Для вычисления средней арифметической используется два способа:среднеарифметический способ и способ моментов. Если частота встречаемости каждой варианты в вариационном ряду равна 1, то рассчитывают среднюю арифметическую простую, используя среднеарифметический способ: Если частота встречаемости вариант в вариационном ряду отличается от 1, то рассчитывают среднюю арифметическую взвешенную, по среднеарифметическому способу: По способу моментов: А – условная средняя,
Если число вариант в вариационном ряду более 30, то строится сгруппированный ряд. Построение сгруппированного ряда: 1) определение Vmin и Vmax Vmin=3, Vmax=20; 2) определение количества групп (по таблице); 3) расчет интервала между группами 4) определение начала и конца групп; 5) определение частоты вариант каждой группы (таблица 2). Таблица 2 Методика построения сгруппированного ряда
Преимущество сгруппированного вариационного ряда заключается в том, что исследователь работает не с каждой вариантой, а только с вариантами, являющимися средними для каждой группы. Это позволяет в значительной степени облегчить расчеты средней. Величина того или иного признака неодинакова у всех членов совокупности, несмотря на ее относительную однородность. Данную особенность статистической совокупности характеризует одно из групповых свойств генеральной совокупности – разнообразие признака. Например, возьмем группу мальчиков 12 лет и измерим их рост. После проведенных расчетов средний уровень данного признака составит 153 см. Но средняя характеризует общую меру изучаемого признака. Среди мальчиков данного возраста есть мальчики, рост которых составляет 165 см или 141 см. Чем больше мальчиков будут иметь рост отличный от 153 см, тем больше будет разнообразие этого признака в статистической совокупности. Статистика позволяет охарактеризовать данное свойство следующим критериями: – лимит (lim), – амплитуда (Amp), – среднеквадратическое отклонение (s), – коэффициент вариации (Сn). Лимит (lim) определяется крайними значениями вариант в вариационном ряду: lim=Vmin Амплитуда (Amp) – разность крайних вариант: Amp=Vmax-Vmin Данные величины учитывают только разнообразие крайних вариант и не позволяют получить информацию о разнообразии признака в совокупности с учетом ее внутренней структуры. Поэтому данными критериями можно пользоваться для приближенной характеристики разнообразия, особенно при малом числе наблюдений (n<30). Наиболее полную характеристику разнообразию признака в совокупности дает среднеквадратическое отклонение (s). Существует два способа расчета среднеквадратического отклонения: среднеарифметический и способ моментов. Среднеарифметический способ:
d – отклонение каждой варианты от средней вариационного ряда, d=V-М. Способ моментов: При вычислении среднего квадратического отклонения может быть использован и приближенный способ по амплитуде вариационного ряда: Таблица 3 Таблица значений k (по С.И. Ермолаеву)
Еще один часто применяемый метод расчета среднего квадратического отклонения при небольшом числе наблюдений по формуле Пирсона: σ =Am*K, где Am – амплитуда вариационного ряда, К – коэффициент Пирсона, находится по таблице 4. Таблица 4 Таблица коэффициентов Пирсона
Среднее квадратическое отклонение оценивает степень вариабельности вариационного ряда прямо пропорционально: чем больше σ, тем вариационный ряд более разнообразен и выборочная статистическая совокупность, из которой он сформирован, более неоднородна, и наоборот, чем меньше σ, тем вариационный ряд менее вариабелен и выборочная статистическая совокупность неоднородна в меньшей степени. Для сравнения разнообразия двух средних величин, выраженных в различных единицах измерения или имеющих различия в величине признаков, используется относительная величина, коэффициент вариации (CV), выпаженный в процентах:
Если CV>20%, то имеет место сильное разнообразие вариационного ряда; CV от 10 до 20% – среднее разнообразие; CV < 10% – слабое разнообразие вариационного ряда. При необходимости оценить симметричность вариационного ряда рассчитывается коэффициент асимметрии (Ка):
Коэффициент асимметрии колеблется от –3 до +3. Если Ка<0, то асимметрия отрицательная, левосторонняя; если Ка>0, то асимметория положительная, правосторонняя; когда Ка=0, ряд симметричен. Задания для самостоятельной работы Задача 1. Длительность лечения в стационаре 45 больных пневмонией (в днях): 25, 11, 12, 13, 24, 21, 22, 21, 23, 22, 21, 14, 14, 22, 20, 20, 15, 15, 16, 20, 20, 16, 16, 20, 17, 17, 19, 19, 19, 18, 18, 18, 18, 19, 19, 17, 17, 18, 18, 19, 26. Составить вариационный ряд, рассчитать среднюю арифметическую по способу моментов и среднее квадратическое отклонение. Задача 2. Частота дыхания (число дыхательных движений в минуту) у 47 мужчин в возрасте 40–45 лет: 12, 14, 13, 15, 16, 16, 16, 19, 19, 20, 20, 20, 19, 13, 15, 12, 15, 13, 15, 12, 17, 12, 17, 16 ,17, 13, 16, 17, 18, 14, 15, 16, 18, 14, 15, 14, 17, 18, 14, 18, 20, 17, 18, 19, 20, 21, 22. Составить вариационный ряд, рассчитать среднюю арифметическую по способу моментов и среднее квадратическое отклонение. Задача 3. Частота пульса (число ударов в минуту) у 55 студентов-медиков перед экзаменом: 64, 66, 60, 62, 64, 68, 70, 66, 70, 68, 62, 68, 70, 72, 60, 70, 74, 62, 70, 72, 72, 64, 70, 72, 66, 76, 68, 70, 58, 76, 74, 76, 76, 82, 76, 72, 76, 74, 79, 78, 74, 78, 74, 78, 74, 74, 78, 76, 78, 76, 80, 80, 80, 78, 78. Составить вариационный ряд, рассчитать среднюю арифметическую по способу моментов и среднее квадратическое отклонение. Задача 4. Длительность нетрудоспособности (в днях) у 35 больных с острыми респираторными заболеваниями, лечившихся у участкового врача-терапевта: 6, 7, 5, 3, 9, 8, 7, 5, 6, 4, 9, 8, 7, 6, 6, 9, 6, 5, 10, 8, 7, 11, 13, 5, 6, 7, 12, 4, 3, 5, 2, 5, 6, 6, 7. Составить вариационный ряд, рассчитать среднюю арифметическую взвешенную и среднее квадратическое отклонение. Задача 5. Лихорадочный период при пневмонии у 32 больных (число дней): 3, 8, 14, 14, 7, 6, 4, 12, 13, 3, 4, 5, 10, 11, 5, 10, 10, 11, 12, 8, 9, 7, 7, 8, 9, 9, 7, 8, 12, 6, 10, 9. Составить вариационный ряд, рассчитать среднюю арифметическую взвешенную и среднее квадратическое отклонение. Задача 6. Результаты измерения длины тела при рождении у 45 девочек (в см.): 48, 51, 53, 49, 51, 53, 51, 48, 52, 51, 53, 49, 50, 53, 48, 52, 50, 52, 50, 52, 50, 51, 52, 53, 47, 52, 48, 48, 52, 50, 46, 46, 54, 55, 56, 48, 52, 52, 51, 53, 53, 48, 50, 54, 48, 50, 50. Составить вариационный ряд, рассчитать среднюю арифметическую по способу моментов и среднее квадратическое отклонение. Контрольные вопросы 1. Что такое средние величины и область их применения? 2. Назовите свойства средних величин. 3. Какие средние величины наиболее часто используются? 4. Что такое вариационный ряд? 5. Какие бывают вариационные ряды? 6. Методика построения простого вариационного ряда. 7. Что такое мода? 8. Дайте определение медианы. 9. Когда рассчитывается средняя арифметическая простая и взвешенная средняя арифметическая? 10. Назовите способы расчета средней арифметической. 11. Среднеарифметический способ расчета. 12. Способ моментов. 13. Методика построения сгруппированного вариационного ряда. 14. Какие величины характеризуют разнообразие признака? 15. Что такое лимит, амплитуда и когда они используются? 16. Область применения и методика расчета среднеквадратического отклонения. 17. Как рассчитать среднеквадратическое отклонение по методике Пирсона? 18. Коэффициент вариации и его оценочные градации. 19. Для чего используется расчет коэффициента асимметрии?
Поиск по сайту: |
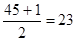 , это место в вариационном ряду занимает варианта равная 11.
, это место в вариационном ряду занимает варианта равная 11.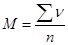 .
. .
.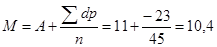 d=V-A, А=Мо=11
d=V-A, А=Мо=11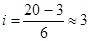 ;
;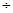 Vmax
Vmax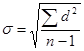 , при n≤30, p=1
, при n≤30, p=1 , при n>30, p>1
, при n>30, p>1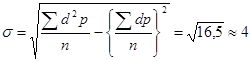 (таблица 2).
(таблица 2).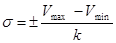 , где Vmax – величина наибольшей варианты вариационного ряда; Vmin – величина наименьшей варианты вариационного ряда; Vmax–Vmin = Am – амплитуда вариационного ряда; k – коэффициент, определяемый по специальной вспомогательной таблице 3, исчисленной С.И. Ермолаевым.
, где Vmax – величина наибольшей варианты вариационного ряда; Vmin – величина наименьшей варианты вариационного ряда; Vmax–Vmin = Am – амплитуда вариационного ряда; k – коэффициент, определяемый по специальной вспомогательной таблице 3, исчисленной С.И. Ермолаевым.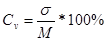 ,
,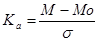 , где Мо – мода, наиболее часто встречающаяся варианта.
, где Мо – мода, наиболее часто встречающаяся варианта.