 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Модели теории катастроф
В начале 70-х годов стал популярен термин «катастрофа», обозначающий скачкообразные изменения, возникающие при плавных изменениях значений параметров. В популярных изданиях теория катастоф рекламировалась как переворот в математике, сравнимый с изобретением дифференциального исчисления. За последние годы появились сотни публикаций, в которых теория катастроф успешно применялась в естествознании и технике. Опубликованы также работы, в которых модели теории катастроф применялись в экономике, психологии, лингвистике, социологии. Один из ведущих российских математиков В.И.Арнольд отмечает, что обоснованность теории катастроф существенно зависит от обоснованности исходных посылок. «Например, в теории хлопков упругих конструкций и в теории опрокидывания кораблей предсказания теории полностью подтверждаются экспериментом. С другой стороны, в биологии, психологии и социальных науках (скажем, в приложениях к теории поведения биржевых игроков или к изучению нервных болезней) как исходные предпосылки, так и выводы имеют скорее эвристическое значение» [1, с. 16]. Чаще всего неприятным сюрпризом для наблюдателя оказывается ситуация, в которой небольшие, постепенные изменения параметров ведут к неожиданно резкому, обвальному изменению поведения системы. Рассмотрим основные положения теории катастроф на качественном уровне, опуская математические детали. Одной из наиболее популярных моделей теории катастроф является катастрофа «сборка», изображенная на рис. 1.
Рис. 1 Катастрофа «сборка»
Здесь наглядно продемонстрированы качественные особенности катастрофического поведения систем. По осям а и b отложены значения независимых переменных, а по оси х - зависимой. Возможным положениям системы соответствует поверхность катастроф. Проекция этой поверхности на плоскость (а, b) дает бифуркационную кривую (бифуркация от лат. bifurcus - раздвоенный). Предположим, что непрерывному изменению значений параметров а и b на рис. 1 соответствует движение по кривой RT. В точке T происходит катастрофа - система скачком переходит с верхнего листа на нижний в точку P. Отметим, что каждому значению параметров а и b внутри бифуркационной кривой соответствуют два различных состояния системы (бимодальность). На поверхности катастроф можно наблюдать явление гистерезиса, когда поведение системы существенно зависит от предыстории процесса. Например, при изменении состояния системы вдоль кривой RT происходит скачок с верхнего листа на нижний - из точки T в точку P. Но при движении вдоль кривой PQ скачок с нижнего листа на верхний произойдет не в точке P, а в точке Q. В работе Постона и Стюарта с помощью теории катастроф исследуется динамика нарушений режима в тюрьме Гартри в течение 1972 г. [17]. Используя факторный анализ, авторы выделили два основных фактора, влияющих на беспорядки: напряженность (чувство разочарования и безысходности, бедственное положение); разобщенность (взаимное отчуждение, отсутствие общения, разбиение на два лагеря). Анализ показал, что с ростом напряженности повышается вероятность волнений, а увеличение разобщенности связано с характером волнений - они становятся более внезапными и яростными.
Рис. 2. Модель волнений в тюрьме Авторы считают, что динамика системы соответствует модели катастрофы «сборка». Из рис. 2 видно, что при низких значениях разобщенности система стремится к устойчивому положению умеренного волнения, но при высоком уровне разобщенности она меняет свое положение скачком с нижнего листа на верхний и обратно. Одно из основных понятий современной нелинейной науки - бифуркация. В математике под бифуркацией понимают изменение числа или устойчивости решений определенного типа для модели, описывающей систему при изменении управляющих параметров [16, с. 170]. В точке бифуркации система как бы делает выбор, который определяет ее дальнейшую эволюцию. Понятие бифуркации описывает процесс перехода постепенных количественных изменений управляющих параметров в качественное изменение состояния системы. Столь емкий термин не мог не завоевать популярность в общественных науках. Так, Лотман считает, что целесообразно рассмотреть два типа социальных процессов. В первом типе социальных процессов события носят внеличностный характер, так как участники процесса практически лишены права выбора. Можно сказать, что люди играют роль частиц в броуновском движении гигантских социальных процессов (развитие общественных формаций, классовые, национальные движения). Второй тип социальных процессов связан с событиями, которые совершаются через сознание людей и с помощью этого сознания. «Человек оказывается перед возможностью выбора поведения и неизменно соотносит свои действия с образом дели, представлением о результатах» [11, с. 3]. Таким образом, там, где социальный процесс предстает как множество альтернатив, выбор между которыми осуществляется интеллектом и волей человека, необходим поиск новых и более сложных форм и моделей причинности. Опираясь на идеи синергетики, Ю. Лотман предлагает рассматривать социальный процесс как многофакторный поток. «Когда достигается точка бифуркации, движение как бы останавливается в раздумье перед выбором пути». Из этой точки может выходить несколько равновероятностных устойчивых траекторий развития. В этом моменте социального процесса люди имеют возможность осуществлять выбор. «Как бы ни были бессильны при нормальном течении истории эти факторы, они оказываются решающими в момент, когда система задумалась перед выбором. Но вмешавшись в общий ход процесса, они сразу же придают его изменениям необратимый характер» [11, с. 3, 4]. Однако не следует забывать, что социальные системы от природных отличает прежде всего то, что эти системы являются когнитивными, способными делать осознанный выбор.
1.2. Синергетика и теория хаоса
В 80-е годы все большее внимание исследователей привлекает проблема самоорганизации, перехода от хаоса к порядку. Немецкий ученый Г. Хакен назвал теорию самоорганизации синергетикой (теория совместного действия). Синергетика изучает такие взаимодействия элементов системы, которые приводят к возникновению пространственных, временных или пространственно-временных структур в макроскопических масштабах. Особое внимание уделяется структурам, возникающим в процессе самоорганизации. Г. Хакен отмечает, что синергетику можно рассматривать как часть общего системного анализа, поскольку и в синергетике, и в системном анализе основной интерес представляют общие принципы, лежащие в основе функционирования системы [22, с. 17]. Таким образом, теория катастроф, системная динамика, теория диссипативных структур «самоорганизовались» в новую междисциплинарную науку - синергетику. Г.Р. Иваницкий считает, что термин «синергетика» мало что поясняет и лучше говорить о «динамических процессах и нелинейных системах, приводящих к хаотизации движения или, наоборот, к его упорядочению и появлению пространственно-временных структур» [7, с. 3] Наряду с теорией относительности, квантовой физикой теория хаоса оказывает все более заметное влияние на парадигмы обществоведения. Высказывается надежда, что теория хаоса послужит углублению взаимопонимания между представителями естественных и гуманитарных наук. Рассмотрим основные понятия синергетики, используемые для изучения поведения нелинейных систем. Система находится в состоянии хаоса, если: - при любых начальных условиях траектории движения становятся апериодическими; - при сколь угодно близких начальных условиях две траектории со временем станут различными. Столь высокая чувствительность к начальным условиям ведет к невозможности прогнозирования поведения системы, что является одной из важнейших характеристик хаоса. Режим называется хаотическим, если расстояние между любыми двумя точками, первоначально сколь угодно малое, экспоненциально возрастает со временем [19]. В древние времена хаосом называли неупорядоченную, бесформенную массу, из которой возникло все сущее. Какая-либо форма, структура может возникнуть из хаоса благодаря внешним целенаправленным воздействиям или под действием сил самоорганизации. «Самоорганизацией называется возникновение упорядоченных структур и форм движения из первоначально неупорядоченных, нерегулируемых форм движения без специальных, упорядочивающих внешних воздействий» [16, с. 61]. Множество точек, к которым притягиваются траектории динамических систем, называется аттрактором. Математики считают, что при качественном анализе поведения динамических систем внимание следует сосредоточить не на переходных процессах, а на установившихся режимах. Математическим образом таких режимов и являются аттракторы. Для устойчивых равновесных систем аттракторами чаще всего является либо точка, тогда переменные не меняются во времени, либо цикл, тогда система испытывает периодические колебания. Если система находится в неустойчивом состоянии, то ее траектории могут притягиваться к странному аттрактору. Странный аттрактор в некоторых случаях похож на клубок траекторий, напоминающих две склеенные друг с другом ленты [2]. Если наблюдать за поведением точки, характеризующей состояние системы, на экране дисплея, то можно увидеть, что точка «бегает» по аттрактору, случайно (хаотично) подается то на левую, то на правую ленту. Странные аттракторы чувствительны к начальным данным. Если выбрать две близкие точки, лежащие на аттракторе, и проанализировать, как будет меняться расстояние между ними с течением времени r(t), то оказывается, что возможны следующие варианты: если аттрактор - особая точка, то г (t) -> О при t->°° (точки сливаются в одну); аттрактор - предельный цикл, г (t) - периодическая функция времени; странный аттрактор г (t) ~ ext (Х>0), г (t)->°° при t~>°° (точки разбегаются с экспоненциальной скоростью) . Таким образом, у странного аттрактора две близкие траектории со временем перестанут быть близкими. Это означает, что как бы точно ни измерялись начальные данные, ошибка со временем станет большой и, следовательно, поведение системы на больших временных интервалах спрогнозировать нельзя. Это явление было названо эффектом бабочки. Странные аттракторы описал метеоролог Лоренц в 1963 г., моделируя задачи прогноза погоды. Из наличия эффекта бабочки вытекает практическая невозможность прогноза погоды: если необходимо предсказать погоду на 1-2 месяца вперед с погрешностью D, то начальные данные должны быть известны с погрешностью D x 105. Переход системы в режим странного аттрактора означает, что в ней наблюдаются сложные непериодические колебания, которые очень чувствительны к незначительным изменениям начальных условий. Такой режим может быть назван хаотическим.
1.3. Диссипативные структуры И. Пригожина
В теории диссипативных структур, развиваемой И. Пригожиным и его школой, первоначально изучались процессы самоорганизации в физико-химических системах [18-20]. До работ Пригожина в естествознании в основном изучались равновесные структуры, которые можно рассматривать как результат статистической компенсации активности микроскопических элементов (молекул, атомов). Если систему с равновесной структурой изолировать от внешней среды, то ввиду инертности данная равновесная структура может существовать бесконечно долго. Однако в биологических и социальных системах ситуация, как правило, другая: система незамкнута, открыта и, более того, существует потому, что она открыта, питается потоками вещества, энергии, информации, поступающими из внешнего мира. В открытых системах случайные флуктуации «пытаются» вывести систему из равновесного состояния. В реальных системах незначительные флуктуации, как правило, подавляются, и система остается стабильной. Если же силы, действующие на систему, становятся достаточно большими и вынуждают ее достаточно далеко уйти от положения равновесия, то состояние системы становится неустойчивым. Некоторые флуктуации могут не затухать, а усиливаться и завладевать всей системой. В результате действия положительной обратной связи флуктуации усиливаются и могут привести к разрушению существующей структуры и переходу в новое состояние. Причем возможен переход и на более высокий уровень упорядоченности, называемый диссипативной структурой. Возникает явление самоорганизации Исследуя динамику сильно неравновесных систем, И. Пригожин приходит к следующим выводам: «Когда система, эволюционируя, достигает точки бифуркации, детерминистическое описание становится непригодным. Флуктуация вынуждает систему выбрать ту ветвь, по которой будет происходить дальнейшая эволюция системы. Переход через бифуркацию - такой же случайный процесс, как бросание монеты. Существование неустойчивости можно рассматривать как результат флуктуации, которая сначала была локализована в малой части системы, а затем распространилась и привела к новому макроскопическому состоянию» [20, с. 56]. Принципы, разработанные Пригожиным для анализа химических процессов, были распространены на широкий класс явлений в физике, молекулярной биологии, процессов эволюции в биологии, а затем и социологии. В настоящее время в естественных науках ведется активное исследование явлений, связанных с возникновением структур, самоорганизацией в простейших нелинейных средах. Делаются попытки выявить прообразы появления организации и в более сложных, в частности социальных, системах. Ученые ведут исследования простейших моделей, анализ которых не может заменить изучение сложных социальных процессов, но может дать исследователям полезную подсказку, помочь подметить скрытые закономерности, сформулировать плодотворные гипотезы. В работе И. Пригожина и И. Стенгерс [20] рассматривается понятие логистической эволюции, т.е. процессов, описываемых логистическим уравнением. Логистическая модель эволюции в настоящее время исследуется в различных областях науки. Как утверждается в [27], хаотические колебания могут возникнуть в период замены старого уклада на новый. Возникновение нестабильности может интерпретироваться как случайный поиск равновесного состояния системой, оказавшейся в ситуации, когда растущие возможности не могут быть реализованы в рамках существующей ниши. Данная модель демонстрирует чередование режимов порядка и хаоса. В период быстрого экономического роста многие компании консолидируются, интегрируются. Корпорации работают как часы, подчиняясь эффективному централизованному управлению. В стадии насыщения под давлением инноваций экономическая система попадает в полосу хаоса. Авторы [20] полагают, что модели, построенные на основе понятия «порядок через флуктуации», будут способствовать более точной формулировке «сложного взаимодействия между индивидуальным и коллективным аспектами поведения». Модели такого типа «открывают перед нами неустойчивый мир, в котором малые причины порождают большие следствия, но мир этот не произволен. Напротив, причины усиления малых событий - вполне «законный» предмет рационального анализа... Если флуктуация становится неуправляемой, это еще не означает, что мы не можем локализовать причины неустойчивости, вызванные усилением флуктуации» [20, с. 270]. В состоянии хаоса поведение системы непредсказуемо. Точнее, нельзя предсказать конкретное состояние, проследить заданную траекторию на длительном временном интервале. Однако вероятностные, усредненные характеристики могут быть спрогнозированы [12]. Странный аттрактор, определяющий хаотическое поведение системы, часто занимает ограниченную область фазового пространства. Поэтому, хотя траектории разбегаются с экспоненциальной скоростью, убежать за границы странного аттрактора они не могут. Следовательно, определение границ области хаоса может позволить получить оценки поведения системы. Чувствительность такой системы позволяет вывести ее из хаотического состояния с помощью очень малых, но точных воздействий [16]. Отметим, что далеко не все теоретики считают, что хаоса следует избегать. Верящие в животворную силу хаоса, наоборот, полагают, что чем он окажется обширнее, глубже, тем более эффективный порядок смогут породить творческие силы самоорганизации. Нельзя не согласится с доктором философских наук В.П.Бранским, заметившим, что «хотя синергетический подход к социальным явлениям завоевал в последней четверти XX века широкую популярность, тем не менее пока он во многих случаях не выходит за рамки философской публицистики» [3, с. 148]. Конечно, знание основных концепций синергетики необходимо современному специалисту, но для практических целей полезней не углубление философской рефлексии, а развитие нелинейной интуиции. 2 Разработка собственной модели
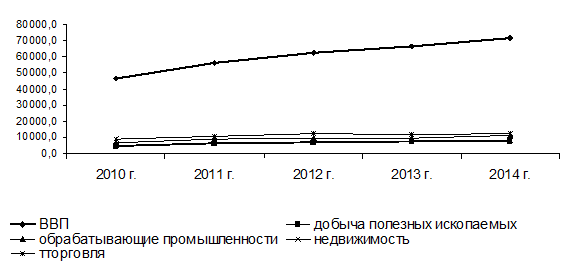
Проведенные Сарыгуловым А.И. исследования показали, что у большинства развитых стран траектории динамики ВВП и добавленной стоимости в традиционных отраслях практически совпадают [21]. Таблица 1 Исходные данные для построения модели [16]
В качестве традиционных отраслей предлагается рассматривать отрасли, имеющие в структуре ВВП удельный вес более 10%: обрабатывающая промышленность, добыча полезных ископаемых, сделки с недвижимостью и торговля.
Рис. 3 Динамика ВВП и отраслевого выпуска
Таким образом, с учетом структурной динамики Валовой внутренний продукт может быть представлен следующей моделью:
где Y0 - фактическое значение ВВП базисного года,
а1 и b1 - параметры линейного уравнения, описывающего тенденцию доли добывающих отраслей в ВВП за весь ретроспективный период; a2 и b2 - параметры линейного уравнения, описывающего тенденцию доли обрабатывающей промышленности в ВВП за весь ретроспективный период; a3 и b3 - параметры линейного уравнения, описывающего тенденцию доли торговли в ВВП за весь ретроспективный период; a4 и b4 - параметры линейного уравнения, описывающего тенденцию доли сектора недвижимости в ВВП за весь ретроспективный период. Среднегодовой коэффициент роста ВВП можно рассчитать по формуле:
где К – коэффициент роста за период:
Линейное уравнение, описывающее тенденцию доли какой-либо отрасли в ВВП, можно представить в общем виде:
где а и b – независимые параметры линейного уравнения.
Независимые параметры линейного уравнения предлагается рассчитывать с помощью встроенных функций MS Ecxel – ОТРЕЗОК (а) и НАКЛОН (b). Спрогнозируем объем ВВП на 2015 г. по рассчитанным параметрам модели:
Таким образом, исходя из предложенной математической модели ВВП, на основании структурной динамики отраслевого состава ВВП предполагается, что суммарный объем производства отрасли достигнет в 2015 г. уровня в 82907 млрд.руб. Ожидаемая динамика ВВП за 2014-2015 гг. составит 116,1% к уровню 2014 года. Прогноз объема ВВП на основании структурной динамики представлен на рисунке.
Рисунок 4 Прогноз ВВП России на 2015 г.
Таким образом, разработанная модель прогнозирования ВВП на основании структурной динамики основных отраслей может быть использована на практике. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Арнольд В.И. Теория катастроф. M., 2010. 2. Базыкин А.Д., Кузнецов Ю.А., Хибник А.И. Портреты 61 бифуркаций: Бифуркационные диаграммы динамических систем на плоскости // Новое в жизни, науке, технике. Сер. «Математика, кибернетика». 2012. №3. 3. Брянский В.П. Теоретические основания социальной синергетики// Петербургская социология. 2011. № 1. С. 148-179. 4. Давыдов А.А., Чураков А.Н. Модульный анализ и моделирование социума. M., 2010. 5. Евин И.А. Синергетика искусства. M., 2013. 6. Иваницкий Г.Р. На пути к второй интеллектуальной революции // Техника кино и телевидения. 2011. № 5. С. 33-40. 7. Иваницкий Г.Р. Синергетика //Новое в жизни, науке и технике. Сер. "Математика, кибернетика". 2012. № 7. 8. Князева Е.Н., Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. M.: Наука, 2014. 9. Концепция самоорганизации в исторической перспективе. M.: Наука, 2014. 10. Кустов В. Математические методы моделирования социально-экономических процессов. – URL: http://www.mogu24.ru/dev.php/edu/document/15751/%D0%9C%D0%B0%D1%82%D0%9C%D0%B5%D1%82_%D0%9C1.pdf 11. Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. M.: Наука, 2010. 12. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент: Введение в нелинейную динамику. M.: Наука, 2010. 13. Митина О.В., Петренко В.Ф. Динамика политического сознания как процесс самоорганизации // Общественные науки и современность. 2014. №5. С. 103-115. 14. Моисеев H. H. Алгоритмы развития. M., 2007. 15. Назаретян А.П. Агрессия, мораль и кризисы в развитии мировой культуры. M., 2010. 16. Национальные счета за 2010-2014 гг. URL.: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/accounts/# 17. Постои Т., Стюарт И. Теория катастроф и ее приложения. M., 2010. 18. Пригожин И. От существующего к возникающему. M., 2011. 19. Пригожин И., Стенгерс И. Время. Хаос. Квант. M.: Прогресс, 2010. 20. Пригожин И., Стенгерс И. Порядок из хаоса: Новый диалог с природой. M., 1996. 21. Сарыгулов А. И. Моделирование структурной динамки макроэкономических систем: автореферат диссертации на соискание ученой степени доктора экономических наук. – СПб, 2012. – URL: http://pandia.ru/text/77/156/24106.php 22. Синергетическая парадигма. Многообразие поисков и подходов. M., 2010. 22. Хакен Г. Синергетика. M., 2015.
Поиск по сайту: |


 , (2.1)
, (2.1) - прогнозное значение ВВП t-го года,
- прогнозное значение ВВП t-го года, - среднегодовой темп роста ВВП,
- среднегодовой темп роста ВВП, (2.3)
(2.3)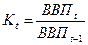 (2.4)
(2.4) (2.5)
(2.5)
