 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
НЕМОНОХРОМАТИЧЕСКОЕ ИЗЛУЧЕНИЕ
Реальное излучение имеет конечную продолжительность и происходит со случайно изменяющимися амплитудой и фазой. Ограниченность по времени и монохроматичность исключают друг друга. Реальную ЭМВ можно представить в виде наложения монохроматических волн с различными частотами в соответствии с принципом суперпозиции полей. С математической точки зрения спектральный состав излучения анализируется с помощью Фурье–преобразований.
Ряд Фурье в действительной форме. В курсе математического анализа было показано, что при достаточно общих условиях, обычно удовлетворимых в физических задачах, периодическая функция f(t) с периодом T может быть представлена рядом Фурье:
где
Интеграл Фурье в действительной форме. Непериодическую функцию f(t) нельзя представить рядом Фурье. Если f(t) кусочно–непрерывна, имеет конечное число экстремумов и абсолютно интегрируема на интервале (–¥, ¥), то
Это выражение может быть получено из (2.1) при T®¥.
Интеграл Фурье в комплексной форме имеет вид:
где (комплексный спектр или просто спектр функции f(t)).
Спектр амплитуд и спектр фаз. Обозначив
из (2.1) получаем:
Совокупность An называется спектром амплитудфункции f(t), а совокупность jn – спектром фаз. Частоты по определению имеют положительные значения. Комплексный спектр (2.5) эквивалентен амплитудному и фазовому спектру
Для вещественной функции f(t)
или
где
Таким образом, периодические функции характеризуются дискретными спектрами, а непериодические – непрерывными. Рассмотрим два примера спектров. 1. Спектр периодически повторяющихся прямоугольных импульсов.
Чем меньше длительность t импульсов по сравнению с периодом их повторения T, тем больше число гармоник (рис.2.1, 2.2).
2. Спектр прямоугольного импульса (рис.2.3, 2.4).
Соотношение между длительностью импульса и шириной спектра. Длительностью импульса называется промежуток времени Dt, в течение которого импульс существенно отличается от 0. Шириной спектра называется интервал частот Dn, на котором амплитуда спектра существенно отлична от 0. Вообще говоря, при таком расплывчатом определении универсального соотношения между Dt и Dn не существует, но есть универсальная закономерность: ширина спектра обратно пропорциональна длительности импульса:
Точное соотношение зависит от формы исследуемого сигнала и от точного определения величин Dt и Dn. Отрицательные частоты. Чаще всего удобнее пользоваться не (2.10), а (2.5), т.е. функцией F(w). Но тогда возникает вопрос о смысле отрицательных частот. F(w) при w > 0 описывает плотность спектральной компоненты частоты w с положительным направлением вращения базисного комплексного вектора еiwt , а F(–w) – плотность спектральной компоненты той же частоты w, но с отрицательным направлением вращения базисного комплексного вектора е–iwt. Таким образом, обращение к отрицательным частотам связано с изменением базисных функций, с помощью которых осуществляется Фурье-преобразование, а именно с переходом к вращающимся комплексным векторам как базисным функциям Фурье-преобразования.
Энергетические спектры. Выразим полную энергию световой волны через интенсивность ее компонент Фурье, вычислив интеграл от E2(t) по времени:
где Ew – Фурье-образ поля E(t) и мы воспользовались (2.4). Изменяя порядок интегрирования по w и по t, и используя (2.5), получаем соотношение, называемое теоремой Планшереля (в разных вариациях в теории спектральных преобразований это соотношение носит название равенство Парсеваля):
Отсюда следует, что полная энергия немонохроматической волны выражается через интеграл по положительным частотам от её спектральной плотности, характеризующей распределение энергии волны по спектру частот. Отметим, что если Ew в соответствии с (2.4) полностью определяет поле E(t), то знание спектральной плотности энергии еще не позволяет восстановить функцию E(t). В энергетическом спектре уже не содержится информация о фазовом спектре. Поэтому данное поле E(t) характеризуется вполне определенным спектром, но одному и тому же спектру могут соответствовать различные E(t). Математическому разложению немонохроматической волны в ряд или интеграл Фурье для нахождения спектральной плотности ее энергии можно сопоставить реальный физический процесс – экспериментальное измерение спектра такой волны с помощью соответствующего анализатора (спектрального прибора). Естественная ширина линии излучения. Простейшей классической моделью излучателя ЭМВ является электрон, колеблющийся с собственной частотой
Решение этого уравнения имеет вид:
где А – амплитуда колебаний, j - начальная фаза, Полная энергия колеблющегося электрона с массой m и зарядом e равна:
Но ускоренно движущийся заряд излучает с мощностью излучения P:
Из-за излучательных потерь энергия электрона уменьшается, а колебания являются затухающими. С учетом того, что уменьшение амплитуды за период колебаний мало по сравнению с амплитудой (испущенная за период энергия мала по сравнению с полной запасенной энергией), по закону сохранения энергии имеем:
где
называется коэффициентом затухания С учетом затухания уравнение (2.17) примет вид:
Решения уравнений (2.21) и (2.23) имеют вид:
т.е. мы получили медленно затухающие колебания. Переходя от величины
Изменение амплитуды во времени приводит к нарушению монохроматичности волны и появлению новых частот в её спектре
Перейдя от напряженности поля к интенсивности, получаем:
Распределение энергии по частотам соответствует лоренцевскому контуру спектральной линии, ширина которого на полувысоте равна коэффициенту затухания g. Лоренцева форма линии излучения образуется при условиях, когда единственным фактором, влияющим на излучения осциллятора, является радиационное («естественное») затухание. Поэтому эту форму линии часто называют естественнойформой линии излучения. Соответствующая линия поглощения имеет такую же форму. Естественная ширина линии очень мала. Для оптических частот С квантовой точки зрения испускание кванта (фотона) происходит в результате перехода излучающего атома из состояния с большей энергией
Т.к. частота определена только в пределах контура излучения, то и энергия возбужденного состояния
Уширение спектральных линий. Естественная форма линии соответствует идеализированной ситуации – атом покоится и не взаимодействует с другими атомами и окружением. Поэтому в реальной ситуации естественную ширину линии прямо измерить крайне трудно, т.к. линия обычно гораздо более уширена за счет движения атомов и взаимодействия их друг с другом. Все виды уширений обычно разделяют на две группы – однородное уширение и неоднородное уширение. При однородном уширении независимо от его природы оно одинаково для всех атомов системы. Наблюдаемая форма линии при излучении всего ансамбля атомов совпадает с формой линии при излучении отдельного атома. Примерами однородного уширения являются естественное уширение и столкновительное уширение в газах. При столкновении излучающих атомов с окружающими атомами или молекулами может произойти обрыв излучаемого волнового цуга или скачок фазы излучения. При этом эффективная длительность цуга уменьшается, а ширина спектра возрастает. При заданных давлении и температуре она статистически одинакова для всех атомов. Ширина столкновительной линии при нормальных условиях примерно на два порядка больше естественной, определяется средним временем между соударениями и описывается лоренцевским контуром. Неоднородное уширение обусловлено различием по тем или иным причинам в условиях излучения отдельных атомов. Тогда наблюдаемая спектральная линия является суперпозицией нескольких однородно уширенных линий, сдвинутых по частоте и соответствующих отдельным группам атомов. Классическим примером неоднородного уширения является доплеровское уширение, характерное для газов при малых давлениях или высоких частотах. Причинами доплеровского уширения являются эффект Доплера, заключающийся в смещении регистрируемой частоты излучения частиц, движущихся относительно наблюдателя с некоторой скоростью, и максвелловское распределение частиц по скоростям. Форма доплеровской линии в хорошем приближении описывается функцией Гаусса. При нормальных условиях в газах ширина доплеровской линии сравнима с шириной столкновительной линии. Другими причинами неоднородного уширения могут являться локальные электрические поля в твердом теле, эффекты Штарка и Зеемана (расщепление и уширение энергетического уровня под действием соответственно электрического и магнитного полей). Модулированные волны. Гармоническое колебание, описывающее волну, характеризуется амплитудой, частотой и фазой. Изменение этих параметров в процессе колебания называется модуляцией, а волны при этом – модулированными. Общий случай амплитудноймодуляции:
Пусть
Тогда
или
т.е. спектральный состав колебания сводится к трем частотам: w (несущая) и w ± W (боковые) (рис.2.5). Если a(t) – периодическая, но не гармоническая функция времени, то спектр состоит из набора частот w ± nW. Общая ширина спектра определяется шириной спектра a(t).
Теперь рассмотрим модуляцию частоты и фазы. Соотношение между частотной и фазовой модуляцией получается как следствие записи фазы колебаний через зависящую от времени частоту:
Тогда
Рассмотрим гармоническую модуляцию частоты
где wо – постоянная частота, около которой происходят колебания частоты с амплитудой Dw и частотой W. Тогда
Если
то
Частотная и фазовая модуляции полностью эквивалентны только тогда, когда они гармонические. При негармонической модуляции эквивалентность невозможна и структура сигналов различна.
Для частотной модуляции: {медленное изменение сигнала (малая W)} Þ Þ{большие колебания по фазе (D= Dw/W)}
Для фазовой модуляции: {медленное изменение сигнала (малая W)} Þ Þ{малые амплитудные колебания частоты (Dw = DF×W)}
Способ осуществления обычно тоже различен. При частотной модуляции изменяется частота самого генератора, а при фазовой модуляции фаза модулируется уже после генератора.
Волновые пакеты. В отличие от распространения в вакууме, в среде скорость ЭМВ меньше c = const и зависит от частоты. Зависимость скорости волны от частоты называется дисперсией. Рассмотрим суперпозицию двух волн:
Фазовая скорость определяется из условия:
Для результирующего поля имеем:
(См. рис.1.3) Если дисперсии нет, то формула (2.43) совпадает с формулой (1.60). Суперпозиция двух и более волн с различными частотами составляет группу волн (волновой пакет). Скоростью группы волн или групповой скоростью u называется скорость движения максимума огибающей амплитуды группы волн. Для (2.43):
Если дисперсия отсутствует, то u = v. При наличии дисперсии групповая скорость отличается от фазовой. Если
Суперпозиция колебаний с эквидистантными частотами. Пусть происходит N колебаний одинаковой амплитуды E0 , частота которых различается на dw. Тогда их суперпозиция имеет вид:
где Энергия волнового пакета даже при N>>1 сосредоточена в сравнительно небольшом интервале частот. Такие волновые пакеты часто называют импульсами.
Общий случай. Рассмотрим импульс, состоящий из бесконечно большого числа монохроматических плоских волн, непрерывно заполняющих интервал частот
(Размерность заключена в амплитуде). Выражение для фазы колебания преобразуем к виду:
Тогда для результирующего поля E получаем:
Получилось уравнение плоской волны с w0 и k0 и медленно меняющейся в пространстве и во времени амплитудой (огибающей) C(z,t), т.к.
Т.к. функция w(k) изменяется в узком интервале волновых чисел вблизи k0 , то (w – w0) можно разложить в ряд:
Ограничившись в разложении первым членом ряда, получаем:
В этом приближении C(z,t) представляет собой суперпозицию низкочастотных монохроматических составляющих, распространяющихся с одинаковой скоростью. Зависимость от координат и времени у всех составляющих одинакова, и волновой пакет (импульс) движется как единое целое (не деформируясь) с групповой скоростью В линейном приближении может случиться, что групповая скорость в некоторых областях частот окажется больше скорости света в вакууме. Это невозможно в соответствии с теорией относительности. Разрешение этого противоречия состоит в том, что в этих областях (т.н. областях с аномальной дисперсией) линейное приближение является недостаточным и необходимо использовать следующие члены разложения. Формула Рэлея. Установим связь между групповой и фазовой скоростями. Используя определения фазовой скорости (2.41) и групповой скорости (2.45), запишем:
Учитывая, что
получаем окончательно выражение, называемое формулой Рэлея (Rayleigh Robert John, 1842–1919), позволяющее по заданному закону дисперсии v(l) получить значение групповой скорости:
Все сказанное для приближения (2.52) справедливо и для формулы Рэлея.
Поиск по сайту: |
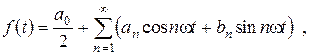 (2.1)
(2.1) (2.2)
(2.2)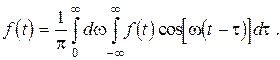 (2.3)
(2.3) (2.4)
(2.4)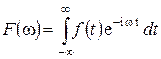 – Фурье-образ функции f(t) (2.5)
– Фурье-образ функции f(t) (2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) и тогда
и тогда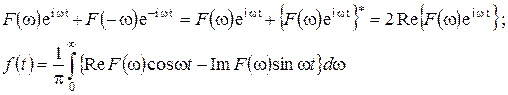 (2.9)
(2.9)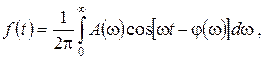 (2.10)
(2.10) (2.11)
(2.11)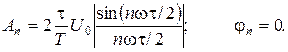 (2.12)
(2.12) Рис. 2.1
Рис. 2.1
 Рис. 2.2
Рис. 2.2
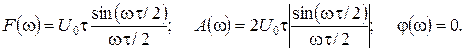 (2.13)
(2.13) Рис. 2.3
Рис. 2.3
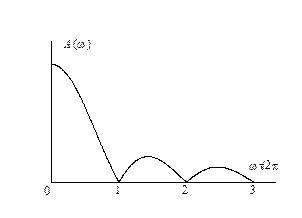 Рис. 2.4
Рис. 2.4
 (2.14)
(2.14) , (2.15)
, (2.15) (2.16)
(2.16) около положения равновесия по гармоническому закону. Уравнение свободных колебаний при этом имеет вид:
около положения равновесия по гармоническому закону. Уравнение свободных колебаний при этом имеет вид: . (2.17)
. (2.17)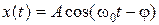 , (2.18)
, (2.18) - отклонение от положения равновесия.
- отклонение от положения равновесия. . (2.19)
. (2.19) . (2.20)
. (2.20)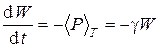 , (2.21)
, (2.21) (2.22)
(2.22) .
.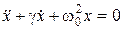 . (2.23)
. (2.23) ; (2.24)
; (2.24)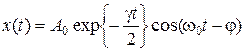 , (2.25)
, (2.25)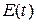 световой волны излучения источника:
световой волны излучения источника: . (2.26)
. (2.26) :
: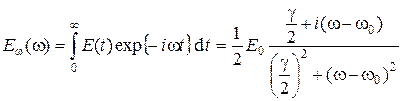 . (2.27)
. (2.27)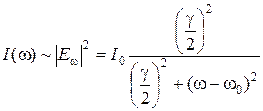 . (2.28)
. (2.28)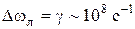 . Поэтому речь идет о квазимонохроматическом излучении
. Поэтому речь идет о квазимонохроматическом излучении  . Лишь в некоторых случаях приходится принимать во внимание конечность естественной линии излучения.
. Лишь в некоторых случаях приходится принимать во внимание конечность естественной линии излучения. в состояние с меньшей энергией
в состояние с меньшей энергией  :
: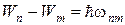 . (2.29)
. (2.29) (2.30)
(2.30) (2.31)
(2.31) (2.32)
(2.32) (2.33)
(2.33) Рис. 2.5
Рис. 2.5
 (фаза). (2.34)
(фаза). (2.34)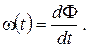 (2.35)
(2.35) (2.36)
(2.36) (2.37)
(2.37) (модуляция фазы), (2.38)
(модуляция фазы), (2.38) (модуляция частоты). (2.39)
(модуляция частоты). (2.39) (2.40)
(2.40) (2.41)
(2.41) . (2.42)
. (2.42) (2.43)
(2.43) (2.44)
(2.44) , то
, то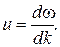 (2.45)
(2.45) (2.46)
(2.46) Рис. 2.6
Рис. 2.6
 – средняя частота колебаний, составляющих волновой пакет (рис.2.6),
– средняя частота колебаний, составляющих волновой пакет (рис.2.6),  – полная ширина частот волнового пакета.
– полная ширина частот волнового пакета.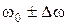 , где
, где  . Диапазону частот
. Диапазону частот  . Тогда для результирующей напряженности поля имеем:
. Тогда для результирующей напряженности поля имеем: . (2.47)
. (2.47) . (2.48)
. (2.48) . (2.49)
. (2.49)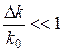 и
и 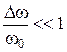 :
: . (2.50)
. (2.50) (2.51)
(2.51) . (2.52)
. (2.52) . Учет членов более высокого порядка в (2.51) показывает, что форма импульса в процессе распространения изменяется.
. Учет членов более высокого порядка в (2.51) показывает, что форма импульса в процессе распространения изменяется.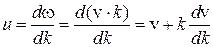 . (2.53)
. (2.53) , (2.54)
, (2.54) . (2.55)
. (2.55)