 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Статистическая обработка результатов определений ⇐ ПредыдущаяСтр 6 из 6
(Правила вычисления нормативных и расчётных характеристик грунтов) По результатам лабораторных работ производится вычисление нормативных и расчётных характеристик грунтов. Нормативное значение Ан характеристики грунта по результатам непосредственных определений, выполняемых в лабораторных условиях, вычисляются по формуле:
где Ai - частное значение характеристики; n - число определений характеристики. Обработка результатов лабораторных испытаний грунтов на срез с целью определения нормативных значений сцепления сн и угла внутреннего трения jн производится путём вычисления методом наименьших квадратов прямолинейной зависимости для всей совокупности опытных величин t в инженерно-геологическом элементе:
где t - сопротивление сдвигу образца грунта; p - нормативное удельное давление, передаваемое на образец грунта. Нормативные значения сн и tg jн вычисляются по формулам:
где
n - число определений. При решении практических задач по расчёту оснований и фундаментов используются расчётные значения характеристик, определяемые по формуле:
где кг - коэффициент безопасности по грунту. Коэффициент безопасности по грунту кг при определении расчётных значений сцепления с, угла внутреннего трения j, временного сопротивления одноосному сжатию Rc и удельного веса грунта g, вычисляется по формуле (для прочих характеристик кг =1):
где r - показатель точности оценки среднего значения характеристики грунта (знак перед величиной r выбирается тот, который обеспечивает большую надёжность данного расчёта основания или фундамента). Показатель точности оценки среднего значения характеристики грунта r вычисляется по формулам:
где ta - коэффициент Стьюдента, принимаемый по табл. 1 в зависимости от заданной доверительной вероятности a и числа степеней свободы: таблица 1 Значения коэффициентов Стьюдента ta
(n - 1) - при вычислении расчётных значений Rc и g; (n - 2) - при вычислении расчётных значений с и j; V - коэффициент вариации характеристики, вычисляемый по формуле:
где s - среднее квадратичное отклонение характеристики, вычисляемое: 1. для с и tg j по формулам:
где
2. для Rc:
3. для g:
Доверительная вероятность a расчётных значений характеристик грунтов принимается равной: · при расчётах оснований по несущей способности a = 0.95; · при расчётах оснований по деформациям a = 0.85. Прежде чем приступить к вычислению нормативных и расчётных значений характеристик, следует выполнить проверку на исключение грубых ошибок в определении частных значений характеристик. Такие значения, вводимые в обработку, искажают статистические показатели грунтов, поэтому их следует исключать. Исключение (выбраковка) производится с учётом статистической проверки, при которой должно выполняться условие:
где Ai и n - статистический критерий, принимаемый в зависимости от числа определений n по табл. 2; sсм - смещённая оценка среднего квадратического отклонения характеристики, определяемая по формуле:
Таблица 2 Значения критерия n
Если условие (17) не выполняется, то значения, выходящие за указанные границы, отбрасываются, а в обработку включают оставшиеся значения. Примеры обработки. Пример № 1. Определить нормативные и расчётные значения удельного веса супеси (было выполнено 12 определений). Результаты определений и необходимые для расчётов вычисления приведены в табл. 3. Определяем среднее арифметическое значение удельного веса грунта:
Делаем проверку на исключение грубых ошибок, для чего по формуле (18) вычисляем sсм:
По табл. 2 для n =12 находим n =2.52, тогда Наибольшее абсолютное отклонение gi от среднего значения Таблица 3
Вычисляем нормативное gн и расчётные значения gII и gI:
По формуле (16) находим среднее квадратичное отклонение:
По формуле (10) вычисляем коэффициент вариации:
Для a = 0.85 (расчёты по деформациям) и числе степеней свободы n-1 = 11 по табл. 1 находим ta = 1.09. По формуле (9) вычисляем показатель точности оценки среднего значения удельного веса супеси:
По формуле (7) определяем коэффициент безопасности по грунту:
По формуле (6) определяем расчётное значение удельного веса супеси для расчётов по деформациям:
Для a = 0.95 (расчёты по несущей способности) и числе степеней свободы n-1 = 11 по табл. 1 находим ta =1.81.Тогда:
Вычисляем расчётное значение удельного веса супеси для расчёта по несущей способности:
Пример № 2. Для инженерно-геологического элемента, сложенного четвертичными покровными суглинками, было выполнено 27 лабораторных определений сопротивления сдвигу t при трёх значениях нормального давления pi = 1; 2 и 3 кгс/см2. Полученные в опытах величины ti приведены в табл. 4 в возрастающем порядке. Таблица 4
Прежде чем приступить к вычислению нормативных и расчётных значений с и j, следует выполнить проверку на исключение грубых ошибок в определениях ti при каждом значении нормального давления. Необходимые для этого подсчёты приведены в табл. 4. Значения статистического критерия n приняты по табл. 2 для n = 9. В результате проверки получено, что при p = 1 кгс/см2 При p = 2 кгс/см2 для одного из значений ti = 1.30 кгс/см2 получено равенство При p = 3 кгс/см2 для значения ti = 1.72 получили Для вычисления нормативных и расчётных значений с и j расчёты следует вести в табличной форме (табл. 5). В первых графах таблицы выписываются экспериментальные значения pi и ti. После вычислений в графах 4 и 5 определяем D, сн и tg jн. Значения в графе 6 получаются путём подстановки найденных значений сн и tg jн в уравнение (2):
jн =18о16’ » 18o;
Таблица 5.
Уравнение прямой графика t = f (p) будет иметь вид: t = 0.33 p + 0.33. Проверим уравнение подстановкой средних значений
Сходимость результатов свидетельствует о правильности вычислений сн и tg jн. После заполнения граф 7 и 8 табл. 5 вычисляются:
Находим расчётные значения с и j для расчётов по второму предельному состоянию. Для a = 0.85 и числа степеней свободы n-2 =24 по табл. 1 находим, что ta = 1.06. Тогда:
jII = 17o13’ » 17o. Для a = 0.95 и n-2 = 24, ta = 1.71;
jI = 16o42’ » 17o.
Поиск по сайту: |
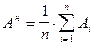 (1)
(1)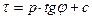 (2)
(2)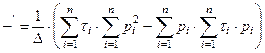 (3)
(3)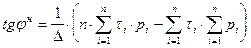 (4)
(4)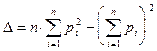 (5)
(5)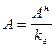 (6)
(6) (7)
(7)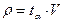

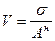 (10)
(10) (11)
(11) (12)
(12)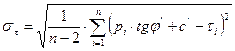 (13)
(13)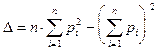 (14)
(14)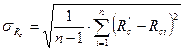 (15)
(15)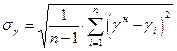 (16)
(16)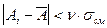 (17)
(17)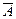 - соответственно частное и среднее арифметическое (нормативное) значения характеристики грунта. Ai содержит все значения после первичной выбраковки (если она производилась);
- соответственно частное и среднее арифметическое (нормативное) значения характеристики грунта. Ai содержит все значения после первичной выбраковки (если она производилась);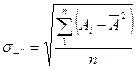 (18)
(18)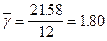 г/см3.
г/см3.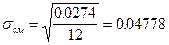
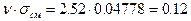 .
. в опыте № 9 (табл. 3) составляет 0.10, что меньше 0.12. Таким образом, ни одно из опытных значений не следует исключать как грубую ошибку.
в опыте № 9 (табл. 3) составляет 0.10, что меньше 0.12. Таким образом, ни одно из опытных значений не следует исключать как грубую ошибку.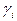
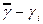
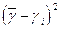
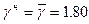 г/см3.
г/см3. .
.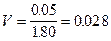 .
.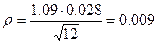 .
. .
. г/см3.
г/см3.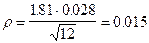 .
.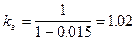 .
.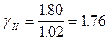 г/см3.
г/см3. ;
;
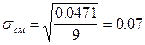 ;
n = 2.35;
;
n = 2.35; 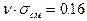 ;
0.10 < 0.16.
;
0.10 < 0.16.
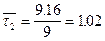 ;
;
 ;
n = 2.35;
;
n = 2.35;  ;
0.28 = 0.28.
;
0.28 = 0.28.
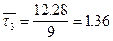 ;
;
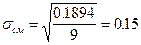 ;
n = 2.35;
;
n = 2.35; 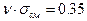 ;
0.36 > 0.35.
;
0.36 > 0.35.
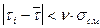 , следовательно, опытные данные не содержат грубых ошибок.
, следовательно, опытные данные не содержат грубых ошибок.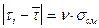 . Следовательно, ti = 1.30 может быть как исключено, так и оставлено. Примем решение - оставить это значение в статистической совокупности.
. Следовательно, ti = 1.30 может быть как исключено, так и оставлено. Примем решение - оставить это значение в статистической совокупности.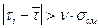 , следовательно, это значение t должно быть исключено как грубая ошибка.
, следовательно, это значение t должно быть исключено как грубая ошибка. (уравнение (5));
(уравнение (5));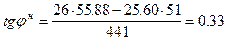 (уравнение (4));
(уравнение (4));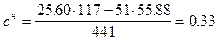 кгс/см2 (уравнение (3).
кгс/см2 (уравнение (3).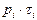
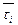
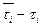

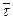 и
и  :
: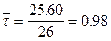 ;
;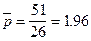 ;
;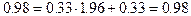 .
.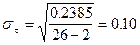 кгс/см2 (уравнение (11));
кгс/см2 (уравнение (11));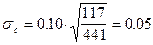 кгс/см2 (уравнение (13));
кгс/см2 (уравнение (13));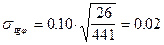 (уравнение (12));
(уравнение (12)); (уравнение (10));
(уравнение (10));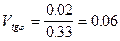 (уравнение (10)).
(уравнение (10)).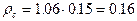 (уравнение (8));
(уравнение (8));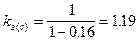 (уравнение (7));
(уравнение (7));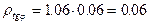 (уравнение (8));
(уравнение (8));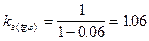 (уравнение (7));
(уравнение (7));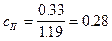 гс/см2 (уравнение (6));
гс/см2 (уравнение (6));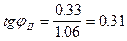 (уравнение (6));
(уравнение (6)); (уравнение (8));
(уравнение (8));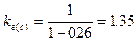 (уравнение (7));
(уравнение (7)); (уравнение (8));
(уравнение (8));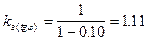 (уравнение (7));
(уравнение (7));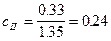 гс/см2 (уравнение (6));
гс/см2 (уравнение (6));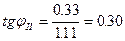 (уравнение (6));
(уравнение (6));