Л а б о р а т о р н а р о б о т а № 2

Розгалужені структури Object Pascal

Мета роботи

Вивчити й набути навичок використання базових керувальних конструкцій та операторів безумовного переходу, умовного переходу та вибору варіанту.

Основні теоретичні відомості

Розгалуженим називається обчислювальний процес, якщо, залежно від певних умов, він реалізовується за однією з певних, заздалегідь передбачених, віток алгоритму.

Для програмної реалізації таких обчислень необхідно використовувати оператори передання управління, котрі дозволяють змінювати порядок виконання операторів програми. У мові Pascal для цього передбачено інструкції: безумовного переходу – goto, умовного переходу – if та вибору варіанта – case. Для запису умови переходу необхідно використовувати логічні (булеві) вирази.

Оператор безумовного переходу goto

Оператор goto(йти до) дозволяє передати керування в будь-яку точку коду (програми), котру позначено спеціальною міткою.

Оператор goto має вигляд:

goto <мітка >;

Мітки, на які можна передавати керування, описують ключовим словом label, після якого йде список міток. Кожна мітка може позначатися припустимим в алгоритмічній мові ідентифікатором або цілим без знака числом від 0 до 9999. Наприклад :

label start, 55, second, a;

означає чотири мітки: start, 55, second, a.

Точка, в яку передається керування, позначена ім'ям мітки, після якої йдуть дві крапки й далі оператор, до якого передається керування. Наприклад, start :S:=0;

Мітка може розташовуватись у будь-якому місці: як перед оператором goto, так і після нього.

Слід уникати передання керування ззовні в середину циклу й заборонено передавати керування до мітки, розміщеної в іншому блоці. Це може призвести до непередбачених наслідків.

Опис міток, самі мітки й оператори goto, які передають на них керування, повинні розміщуватися в межах області видимості ( блоку).

Розумне застосування оператора goto робить структуру програми більш прозорою і спрощує її розуміння.

Логічні вирази

Логічні вирази – це послідовність логічних зміних, констант, відношень, з’єднаних логічними (булевими) операціями, результатом яких є логічне значення. Логічні значення позначаються стандартними іменами True (істина) та False (хибність), причому True<False. Логічні константи теж мають тільки два значення: True та False.

Логічні змінні − це змінні, які набирають одного з цих значень. У розділі змінних вони повинні бути описані як Boolean, наприклад:

Var p,q : boolean;

Стандартні функції зі значеннями логічного типу подано у таблиці 2.1.

Таблиця 2.1 – Стандартні функції логічного типу

Найпростішими логічними виразами є відношення (порівняння).

2.2.1 Операції відношення

Операції відношення використовуються для порівняння двох виразів. Вони повертають значення true(істина), якщо вказані відношення виконуються і false(хибність) – в іншому разі. Операції відношення подано в табл. 2.2.

Таблиця 2.2 Операції відношення

Тип результату у всіх випадках Boolean (логічний).

Операнди повинні мати сумісні типи, за винятком типів real та integer, які можуть порівнюватись один з одним. Рядки порівнюють за розширеними кодами множини символів ANSI.

Символьний тип трактують як рядки одиничної довжини. Упаковані рядки можна порівнювати лише за однакової кількості символів. Якщо упакований рядок з n символів порівнюють з типом string, то він трактується як рядок з довжиною n. Операції <, >, <= й >= можна застосувати до операндів Pchar, тільки якщо обидва вказівники вказують на один й той самий масив символів.

Приклади відношень та їх результатів подано в табл. 2.3.

Таблиця 2.3 – Приклади результатів відношень

2.2.2 Булеві операції

У булевих операціях використовують операнди булевих типів і повертають результат булевого типу − Boolean (табл. 2.4):

Таблиця 2.4 – Булеві операції

Компілятор Delphі підтримує два режими розрахунків операцій AND і OR: повний і скорочений. У повному режимі усі логічні вирази обчислюють до кінця, навіть якщо після розрахунків першого операнда результат визначено. У скороченому режимі розрахунок переривається, як тільки результат дорівнюватиме True. Тобто, якщо перший операнд дорівнює True і результат визначено, то в скороченому режимі розрахунок перерветься без обчислень другого операнда. Операція компілятора {$B-}, що працює без додаткових вказівок, забезпечує скорочений режим розрахунків, а операція {$B+}–повний. Режим повних розрахунків можна також установити опцією Compile Boolean Evaluatіon у вікні компілятора.

2.2.3 Порозрядні (побітові) булеві й сдвигові операції

Логічні порозрядні операції оперують з двійковими представленнями цілих чисел, тобто працюють із двійковими розрядами операндів (табл.2.5):

Таблтця 2.5 Порозрядні (побітові) булеві й сдвигові операції

Наприклад, Х 001101

Y 100001

X or Y 101101

X and Y 000001

При порозрядних операціях чинні є такі правила. Результат, що визначає not, має той самий тип, що й її операнд. Результат операцій and, or, xor має цілий найменший тип, що включає всі значення типів обох операндів. Вирази x shl y і x shr y зміщують значення х вліво і вправо на y бітів. Це еквівалентне помноженню х на 2^y . результат має той самий тип що і х.

Розглянемо приклади. Якщо операнди А і В будуть мати тип Byte, то виконання операцій при А=11, У=2 дає результати, подані в таблиці 2.6.

Таблиця 2.6 Десяткові та двійкові значення логічних операцій

Результати логічних операцій, що використовують до операндів цілого типу (порозрядно 1,0) і логічного типів (true, false), подано в таблиці 2.7.

Таблиця 2.7 – Результати операцій над даними цілого та логічного типу

На рисунку 2.1 зображено логічні блоки у відповідності з міжнародними стандартами.

a a+b схема “АБО”, що реалізує операцію логічного додавання

b

а a*b схема “І”, що реалізовує операцію логічного множення

b

а а схема “НІ”, що реалізовує операцію інверсії

Рисунок 2.1 – Стандартні логічні блоки

З логічних блоків складаються складні логічні пристрої. Перед побудовою логічних схем пристроїв логічну функцію мінімізують, тобто приводять до більш простого виду, користуючись співвідношеннями алгебри логіки (булевої алгебри).

Для логічних схем “АБО”, “І” та “НІ” існують технічні схеми, що реалізовують їх на реле, півпровідникових або ферритових елементів. У сучасних комп'ютерів звичайно використовують системи інтегральних елементів, у яких з метою більшої уніфікації в якості базової логічної схеми застосовують одну зі схем: “І”−”НІ” (штрих Шеффера), “АБО”−”НІ” (стрілка Пирса) або “І”−”АБО”−”НІ”.

2.2.4 Пріоритети й асоціативність операцій

У складних логічних виразах послідовність розрахунків визначають звичайними способами. За відсутності дужок послідовність обчислень логічних виразів визначають за старшинством та асоціативністю операцій.

За старшинством (пріоритетом) логічні операції поділяють у спосіб, поданий в таблиці 2.8.

Таблиця 2.8 – Пріоритети логічних оперцій

Операції з більш високим пріоритетом виконуються раніш за операції з більш низьким пріоритетом.

Якщо поряд розміщено декілька операцій з однаковими пріоритетами, то послідовність обчислень визначається асоціативно, яка у всіх операцій у Object Pascal є однакова − зліва направо.

Наприклад: х=y or x=z

У цьому разі послідовність операцій визначають так:

x = ( y or x ) = z

тому що or має вищій пріоритет, ніж операція =. Після виконання or операція = виконається зліва направо.

Порівняно з арифметичними операціями (+, -, *, /, DIV, MOD) операції відношення мають менший пріоритет.

Наприклад, значення відношення 2*5<=17 div 3 є false, а відношення 7+3>16-4*3 – true.

Слід пам'ятати, що до операндів дійсного типу не варто застосовувати операцію відношення = (дорівнює), тобто ця умова може не виконатись через неточне представлення дійсних чисел у пам'яті комп'ютера та неуникних помилок округлення при обчислюванні виразів. Тому відношення а1=а2 слід замінювати відношенням

abs(a1−a2)<eps,

де eps − певна мала величина, котра характеризує похибку округлення.

Дві логічні операції можуть бути записані поряд, якщо другою з них є операція not, наприклад:

x1 and not x2

Логічні операції та операції відношення можуть зустрічатись в одному виразі. Причому відношення, що стоять зліва та справа від знаку логічної операції, має бути взято в дужки, оскільки логічні операції є вищі за пріоритетом.

За допомогою дужок можна змінювати порядок розрахунків. Наприклад, у логічному виразі

1 6 4 2 5 3

(-3>=5) or not (7<9) and (0<=3)

цифрами зверху показано послідовність виконання операцій: результат виконання операції 1 − False, операції 2 − True, операції 3 − True, операції 4 − False, операції 5 − False, операції 6 − False. Тобто логічний вираз має значення False.

Для деяких типів у Pascal є додаткові операції, що дозволяють формувати складніші умови. Наприклад, для множини визначена операція IN (зарезервоване слово), яка перевіряє, чи входить конкретне значення в множину:

x:=[2,4,6,8,10];

Вираз 2 in x має значення true.

Вираз 5 in x має значення false.

Цей спосіб виконання перевірки більш наглядний. Наприклад, замість

(i>=1) and (i<=10),

використовуючи операцію in, можна записати

i in [1…10]

Виконуються ці перевірки теж значно ефективніше.

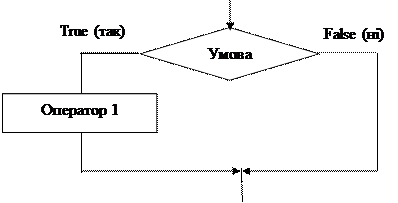
Умовний оператор

Умовний оператор у Pascal дозволяє виконати один чи два оператора, які входять до нього, залежно від значення логічного виразу.

Оператор має вигляд :

if < логічний вираз > then <оператор1 > else < оператор2>;

де if (якщо), then (то), else (iнакше) – службові слова;

оператор1, оператор2 - прості чи складені оператори мови.

Оператор if – це єдине речення, тому ані перед then, ані перед else крапку з комою ставити не можна. Порядок виконання умовного оператора показано на рис.2.2

Рисунок 2.2 – Схема алгоритму умовного оператора переходу

Як видно зі схеми, якщо значення логічного виразу дорівнює true, то виконується оператор1, якщо логічний вираз – false, то виконується оператор2 (оператор 1 пропускається ). Далі у кожному разі виконується оператор 3, що стоїть за оператором if. Наприклад, фрагмент програми обчислення функції

y =

має вигляд

if x>0 then y:=ln(x) else y:=exp(x);

Тут логічний вираз – відношення x>0, оператор 1 і оператор2 − оператори присвоєння y:=ln(x) і y:=exp(x).

Існує скорочена конструкція if (без else):

if <логічний вираз> then <оператор1>;

Порядок виконання цього оператора показано на рис. 2.3.

Якщо логічний вираз набирає значення False, то виконується наступний за if оператор.

У якості операторів можна використовувати складні оператори. Наприклад (фрагмент програми):

if j:=0 then

begin ShowMessage (‘Ділення на нуль’); Result:=0;

end // крапка з комою не ставляться !!!

else Result:=I/j;

Рисунок 2.3 Схема скороченого оператора умовного переходу

Умовні оператори можуть бути необмежено вкладеними один в одного.

В деяких випадках складно розібратися, у якій послідовності виконуються такі вкладені оператори.Наприклад:

if a>b then

if a>e then c:=1

else c:=2;

Тут важко зрозуміти, в якому разі виконується оператор С:=2,: коли хибна є умова a>b або коли вона є правдива, але хибна є умова a>e.

У таких випадках чинне є правило: else належить до найближчого оператора if.

У даному прикладі частина else c:=2 належить до найближчого оператора if a>e then, а не до оператора if a>b then.

Треба намагатися записувати подібні вкладені оператори максимально наочно, використовуючи відступи із пропусків, уникати заплутаних складових і великого рівня вкладеності.

Приклад. Обчислити значення функції за формулою:

Для програмної реалізації цих виразів можна використати конструкцію умовного оператора, оскільки тут умови є альтернативними, тобто взаємно доповнюють і виключають одна одну.

Перший варіант:

if x> 0 then

if x>= 1 then y:=sqrt (x)/2

else y:=exp(1/3*ln (x))/3

else y:=exp(1/4*ln(abs(x)))/4;

Другий варіант, простіший, може бути виконано за допомогою логічних операцій і послідовностi незалежних умовних операторів:

if x<=0then y:=exp(1.4*ln(abs(x)))/4;

if (x>0) and (x<1) then y:=exp(1.3*ln(x))/3;

if x>=1then y:=sqrt(x)/2;

На відміну від попереднього випадку, тут завдання розв’язано за допомогою трьох умовних операторів, тоді як там використано лише один оператор, але з укладеннями.

Другий варіант є більш переважним з точки зору зручності читання та наочності програми.

Поиск по сайту: